一、定义:
连通图:
如果有路径使得顶点i,j相连。则称顶点i,j连通。
最小生成树:
在含有n个顶点的连通图中,选取n-1个边,构成一个极小连通子图,使得各个边的权值和最小,则这个最小连通子图称为最小生成树。如图所示:

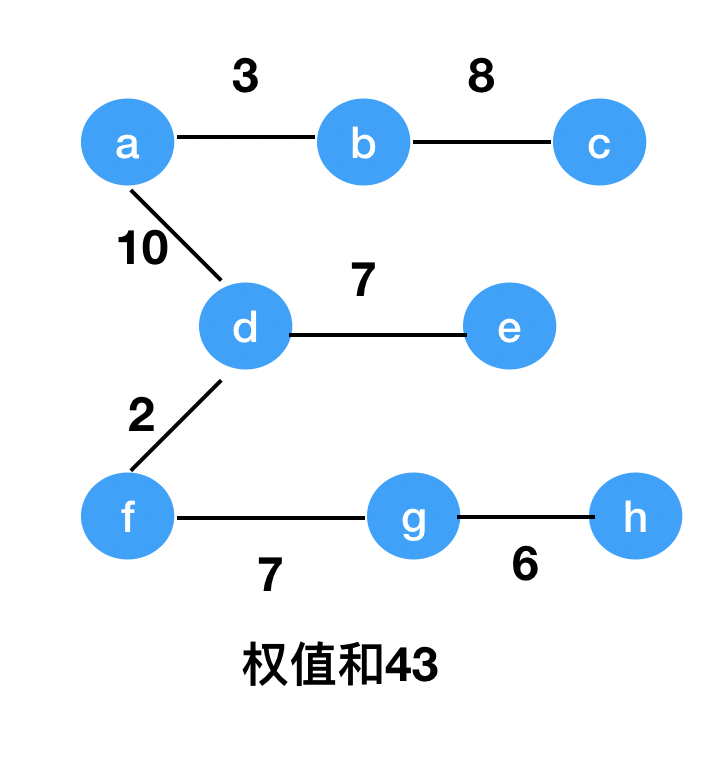
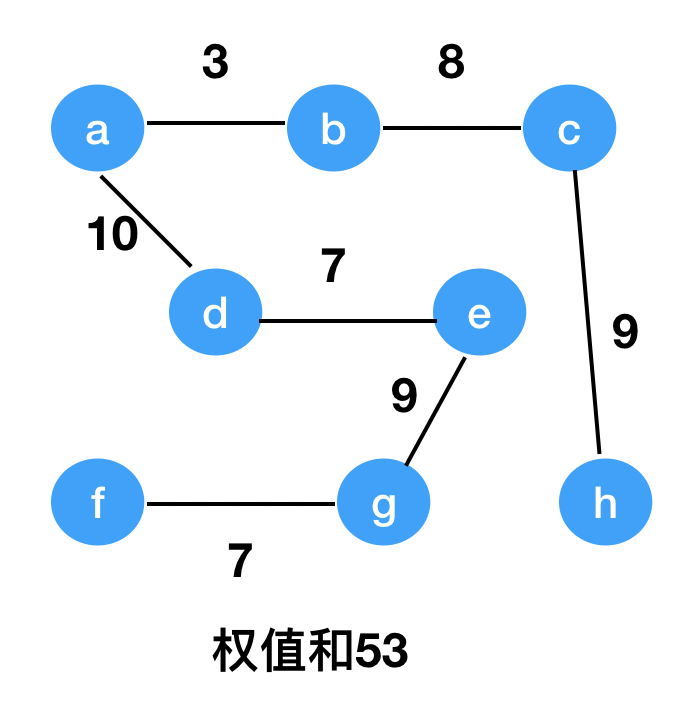
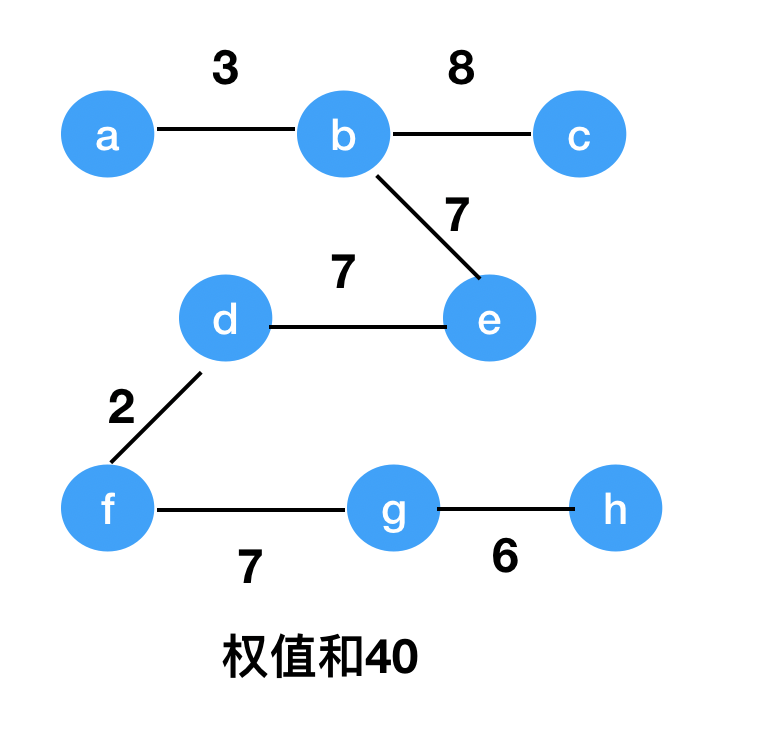
则可以看出权值和为40的这个图为最小生成树。
二、解法
1、Prime算法
- 首先定义两个集合U,V用来存放顶点。V用来存放已经加入的点,U用来存放没有加入的点。
- 从起点开始,将其放入集合V中
- 以V为搜索框架,在U中寻找V不存在的点,使得点v与点u的边权值最小,将边vu加入集合E中
- 重复此步骤,直到V、U顶点一样
图解:

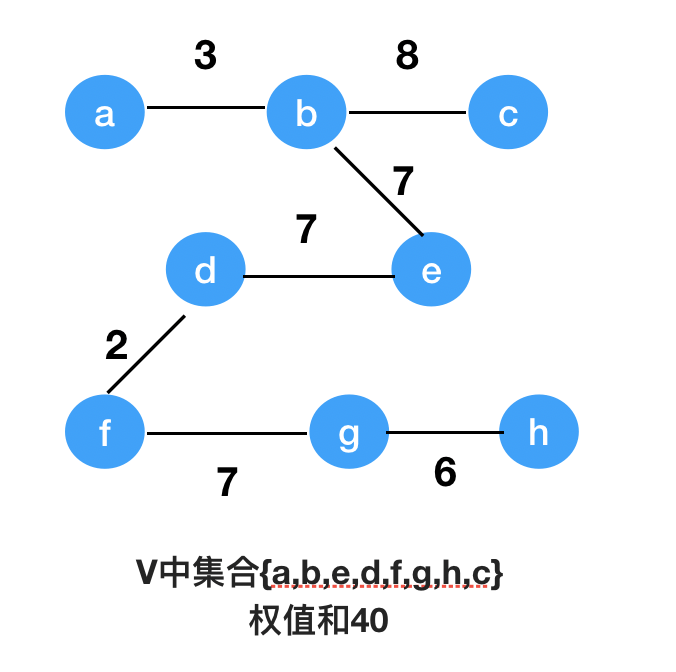
Code:
1 package algorithm; 2 3 import java.util.ArrayList; 4 import java.util.List; 5 6 public class Prime { 7 private static final int INF = 0x7fffffff; 8 9 public static class Edge { 10 char from; 11 char to; 12 int weight; 13 14 public Edge(char from, char to, int weight) { 15 this.from = from; 16 this.to = to; 17 this.weight = weight; 18 } 19 } 20 21 public static class Graph { 22 char[] nodes; 23 int[][] matrix; 24 25 public Graph(char[] nodes, int[][] matrix) { 26 this.nodes = nodes; 27 this.matrix = matrix; 28 } 29 } 30 31 public static List<Edge> prime(Graph graph) { 32 int n = graph.nodes.length; 33 boolean[] visited = new boolean[n]; 34 visited[0] = true; 35 List<Edge> res = new ArrayList<>(); 36 37 for (int a = 0; a < n-1; a++) { 38 int from = 0, to = 0, min = INF; 39 for (int i = 0; i < n; i++) { 40 if (visited[i]) { 41 for (int j = 0; j < n; j++) { 42 if (!visited[j] && j != i && graph.matrix[i][j] < min) { 43 min = graph.matrix[i][j]; 44 from = i; 45 to = j; 46 } 47 } 48 } 49 } 50 visited[to] = true; 51 res.add(new Edge(graph.nodes[from], graph.nodes[to], min)); 52 } 53 54 return res; 55 } 56 57 public static void main(String[] args) { 58 char[] nodes = { 59 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h' 60 }; 61 62 int[][] matrix = { 63 {0, 3, INF, 10, INF, INF, INF, INF}, 64 {3, 0, 8, INF, 7, INF, INF, INF}, 65 {INF, 8, 0, INF, INF, 9, INF, INF}, 66 {10, INF, INF, 0, 7, 2, 14, INF}, 67 {INF, 7, INF, 7, 0, INF, 9, INF}, 68 {INF, INF, INF, 2, INF, 0, 7, INF}, 69 {INF, INF, INF, 14, 9, 7, 0, 6 }, 70 {INF, INF, 9, INF, INF, INF, 6, 0 } 71 }; 72 73 Graph graph = new Graph(nodes, matrix); 74 75 List<Edge> res = prime(graph); 76 for(Edge edge : res){ 77 System.out.println("from " + edge.from + " to " + edge.to + " wight " + edge.weight); 78 } 79 } 80 }
结果:
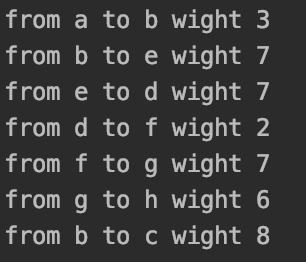
2、Kruskal算法
步骤
- 将图G的边按照权值从小到大排序得到边的集合 E,初始化极小连通子图V
- 遍历E,从E中取出每个边e,如果e中的两个点和V不属于统一连通分量(将e加进V中不构成环),则将e加入V中
- 重复上述过程,直到已经加入了n-1条边,其中n为顶点个数。
图解
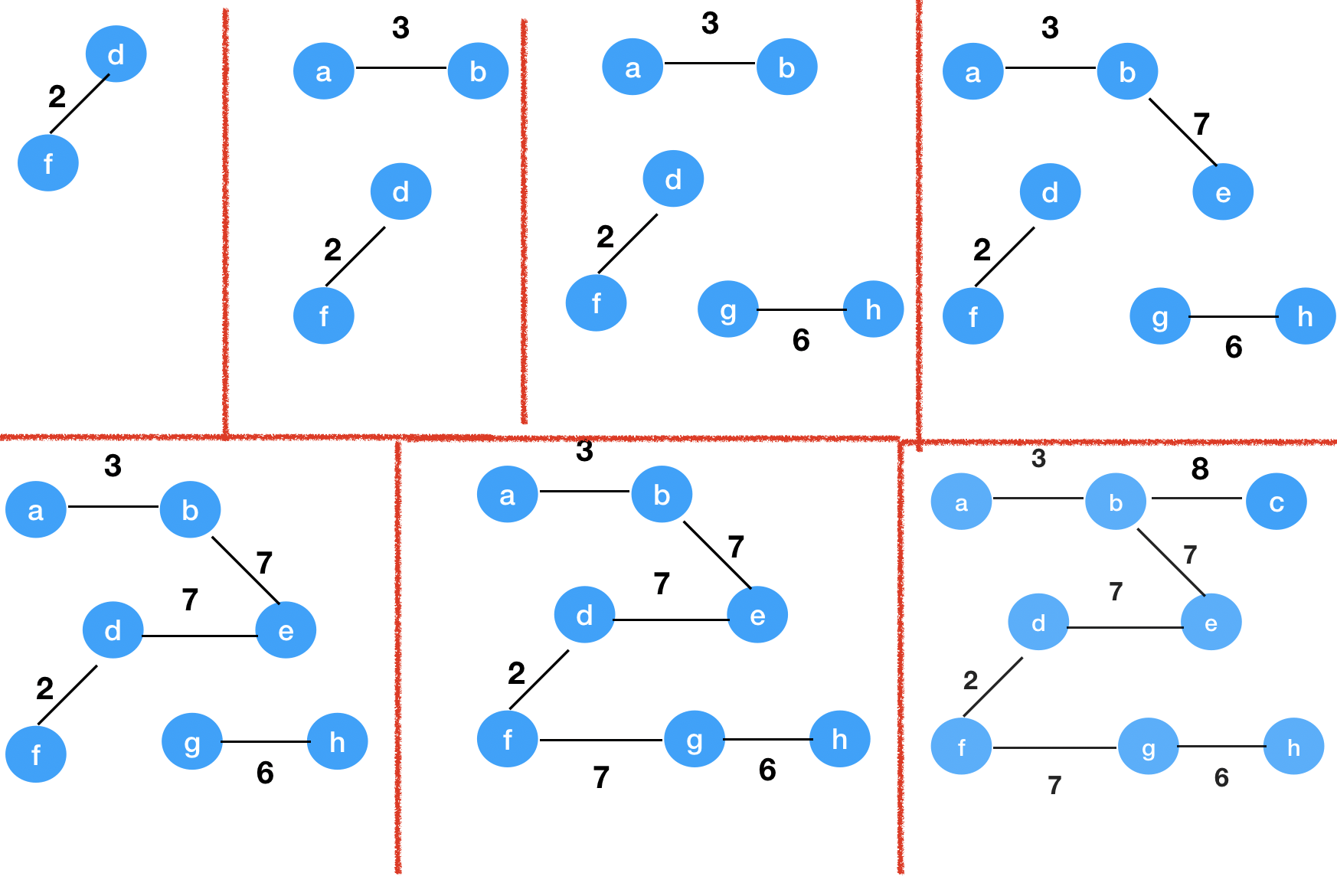
如果要加入一个边e到一个图G,判断新图有没有环:
- 记录图G中所有点f的终点t
- 分别寻找边e两点a,b的终点
- 如果边a,b的终点一样则,a,b已经在一个连通图中,如果加入e边,则形成了环
- 现有算法并查集算法(合并-查找)
Code:
1 package algorithm; 2 3 import java.util.ArrayList; 4 import java.util.Collections; 5 import java.util.List; 6 7 public class Kruskal { 8 private static int[] endsOfNode; 9 private static int INF = 0x7fffffff; 10 11 //定义边类 12 public static class Edge implements Comparable<Edge> { 13 int from; 14 int to; 15 int weight; 16 17 public Edge(int from, int to, int weight) { 18 this.from = from; 19 this.to = to; 20 this.weight = weight; 21 } 22 23 @Override 24 public int compareTo(Edge o1) { 25 return this.weight - o1.weight; 26 } 27 } 28 29 //定义图类 30 public static class Graph { 31 char[] nodes; 32 int[][] matrix; 33 34 public Graph(char[] nodes, int[][] matrix) { 35 this.nodes = nodes; 36 this.matrix = matrix; 37 } 38 } 39 40 //得到一个连通图的终点, 递归更新每一个点的终点,查找操作,并且将每一个点的终点都统一成一级结构,64,65,70行为合并 join操作 41 public static int getEndOfNode(int index) { 42 if (endsOfNode[index] != index) endsOfNode[index] = getEndOfNode(endsOfNode[index]); 43 return index; 44 } 45 46 public static List<Edge> kruskal(Graph graph) { 47 int n = graph.nodes.length; 48 endsOfNode = new int[n]; 49 50 for (int i = 0; i < n; i++) endsOfNode[i] = i; 51 52 53 List<Edge> edges = new ArrayList<>(); 54 for (int i = 0; i < n; i++) 55 for (int j = i + 1; j < n; j++) 56 if (graph.matrix[i][j] != INF) 57 edges.add(new Edge(i, j, graph.matrix[i][j])); 58 59 Collections.sort(edges); 60 61 int c = 0; 62 List<Edge> res = new ArrayList<>(); 63 for (Edge edge : edges) { 64 int x = getEndOfNode(edge.from); 65 int y = getEndOfNode(edge.to); 66 67 if(x == y) continue; 68 if (c++ == n - 1) break; 69 res.add(edge); 70 endsOfNode[x] = y; 71 } 72 return res; 73 } 74 75 76 public static void main(String [] args){ 77 char[] nodes = { 78 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h' 79 }; 80 81 int[][] matrix = { 82 {0, 3, INF, 10, INF, INF, INF, INF}, 83 {3, 0, 8, INF, 7, INF, INF, INF}, 84 {INF, 8, 0, INF, INF, 9, INF, INF}, 85 {10, INF, INF, 0, 7, 2, 14, INF}, 86 {INF, 7, INF, 7, 0, INF, 9, INF}, 87 {INF, INF, INF, 2, INF, 0, 7, INF}, 88 {INF, INF, INF, 14, 9, 7, 0, 6 }, 89 {INF, INF, 9, INF, INF, INF, 6, 0 } 90 }; 91 92 Graph graph = new Graph(nodes, matrix); 93 94 List<Edge> res = kruskal(graph); 95 for(Edge edge : res){ 96 System.out.println("from " + nodes[edge.from] + " to " + nodes[edge.to] + " wight " + edge.weight); 97 } 98 } 99 }
结果:
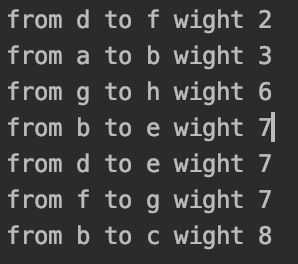
3、并查集算法
1、
在kruskal算法中,如果我们要新加入一条边到一个子图当中,需要判断如果加入改边,是否会形成环。如图所示,如果已经加入了边E(a,b), E(b,c), 现在要加入E(a,c)。需要先判断加入边E(a,c)是否形成了环,即判断点a,c是否在同一个连通子图中。

2、
那么如何判断呢?我们可以构造一个连通图。然后在这个联通图中,从边的一点出发去寻找另一个点。如果找到这两个点在同一个连通图中,否则不在一个连通图中。

这是一个简单粗暴最容易想到的方法。如果A,B在同一个连通子图中,每次查找的时间复杂度是O(n2),n为连通子图的节点个数。
3、Can we do better?
如果能设计一个结构,使得在一个连通子图中所有子节点都指向一个父节点,那么查找的时间复杂度会是O(1),更新每个子节点的时间复杂度是O(n).
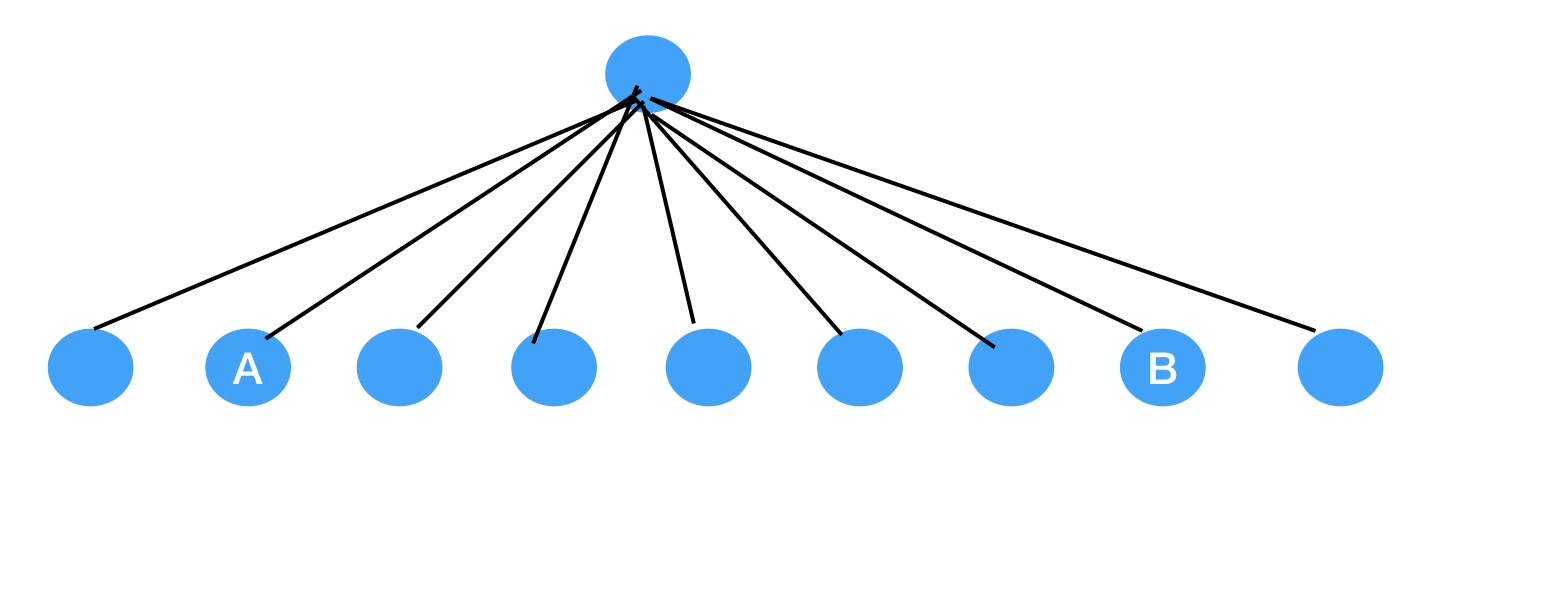
实际做法是
- 记录每个子节点C的父节点F
- 如果父节点F有了父节点G,则更新F的每一个子节点的父节点为G
- 要保证边两端节点命名的顺序,例如E(a,b) ,E(b,c)要有字母顺序
4、Code(非递归版本)
public int find(int node){ int end = node; while (end != ends[end]) end = ends[end]; //查找根节点 while (node != end){ //更新每个子节点的父节点为 end int nt = ends[node]; ends[node] = end; node = nt; } return end; } public void join(int a, int b){ int ae = union(a); int be = union(b); if (ae != be){ ends[ae] = be; //插入边的右节点 为 左节点的父节点 } }
递归代码更简洁:
public int find(int node){ if(ends[node] != node) ends[node] = find(node); return node; } public void join(int a, int b){ int ae = union(a); int be = union(b); if (ae != be){ ends[ae] = be; //插入边的右节点 为 左节点的父节点 } }