题目链接
众所周知,这道题和积木大赛是同一道题
题意就是给出一段自然数序列,每次操作((L,R))把区间([L,R])的数全部减一,不允许出现负数,问把序列变为零的最小操作次数
贪心做法
样例
6
4 3 2 5 3 5
大概长这个样子

我们考虑第一列的四块格子,最少需要(4)次操作给消除掉
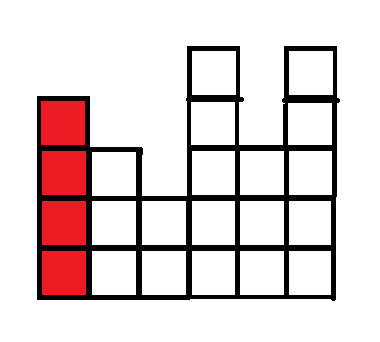
在考虑第二列的(3)个格子时,发现都可以在第一列的(4)次操作中一起消除掉
第三列的格子也都可以一起消除掉
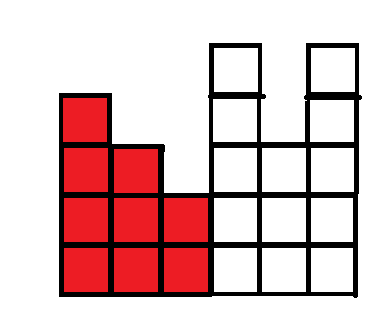
考虑第四列,我们可以发现,第四列下面的两个格子在前面的操作中可以一起消除,但是上面的三个是至少再进行三次操作才能消除的
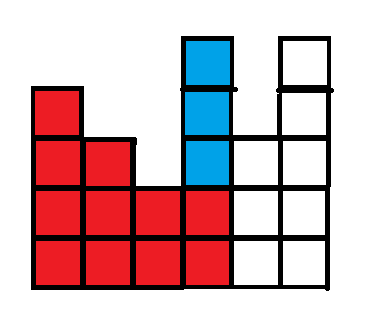
而第五列下面的两个格子在第一列的操作中可以消除,上面的一个格子可以在第四列的操作中删除

考虑第六列,上面的(2)个格子是前面操作消除不了的,需要(2)次操作
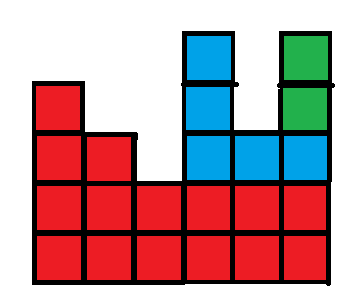
那么答案就是(4+3+2=9)

这样大概可以总结出做法:当(a_{i-1}<a_i)时,(ans+= a_i - a_{i-1})
贪心证明
下面用差分序列给出这个贪心的证明:
我们对原序列({a_i})维护一个差分数组({diff_i})
原序列不妨在最后加一个(0),
6
4 3 2 5 3 5 0
差分数组是
4 -1 -1 3 -2 2 -5
每次操作可以表示为(diff[L]--),(diff[R+1]++)
最终的状态就是差分数组全部变成(0)
首先,每次操作最多让一个大于零的(diff_i) (-1),所以 最优解(ans>=sum(diff_i,diff_i>0))
下面要证明 (ans=sum(diff_i,diff_i>0))
(a_{n+1}=0) => (sum(diff_i)=0) => (sum(diff_i,diff_i>0)+sum(diff_i,diff_i<0)=0)
我们只要每次操作能让一个大于(0)的(diff_i) (-1),同时后面一个小于(0)的(diff_i) (+1)才能够使(ans=sum(diff_i,diff_i>0))
然而有一个限制条件:(a_L)~(a_R)之间没有零 否则这个操作就是不合法的
我们可以利用以下性质构造解法:
性质1:由题意知任意时刻(a_i>=0),若(diff_i>0) 则(a_i>a_{i-1}>=0),得(a_i>0)
性质2:由于(a_{n+1}=sum(diff_i)=0),对于一个大于零的(diff_i),(sum(diff_{1})~(diff_{i})=a_i>0),它的后面一定存在小于零的(diff_i)
于是有:每次选一个大于零的(diff_i)作为操作的左端点(L),它右边的第一个小于零的(diff_j)作为(R+1),已知(a_L>0),([L,R])中任意(diff_k>=0),可得任意(a_k)属于([L,R]),(a_k>=a_{k-1}>=a_L>0),因此该操作合法
所以存在至少一种操作方法可以在(sum(diff_i,diff_i>0))次操作后使得(diff)序列全部为(0),(ans=sum(diff_i,diff_i>0))