考文献:
Geiger A, Moosmann F, Car Ö, et al. Automatic camera and range sensor calibration using a single shot[C]//Robotics and Automation (ICRA), 2012 IEEE International Conference on. IEEE, 2012: 3936-3943.
代码网站:http://www.cvlibs.net/software/libcbdetect/

棋盘格角点定位: 棋盘格角点有很明显的特征, 黑白交叉,常用的方案是使用角点检测算法, opencv有提供对应的算法, 但是这种算法对于模糊、噪点多的
图像稳定太差, 虽然能够对角点进行检测,但是同时会引入其他不需要的点,需要配合筛查算法来进行过滤;
文章开头给出的论文提供了一种角点检测算法, 它是基于生长的检测方案, 通过研究作者代码发现该算法的稳定性非常好, 能够定位亚像素级的角点;
下面按照代码流程看看它是怎么实现的:
1. 角点粗检测(滤波 + 非极大抑制);
针对棋盘格角点的特征, 黑白交叉, 构建高斯滤波核(选取3个sigma, 两种布局);
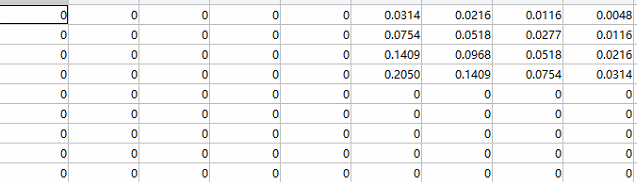
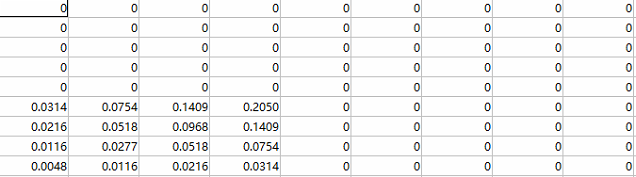
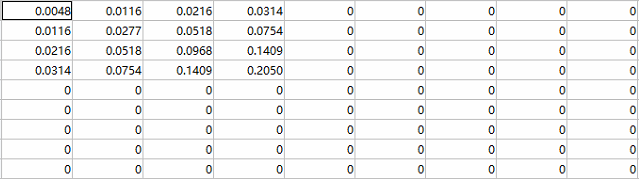
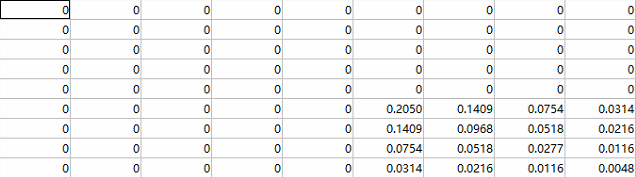
上面是同一个sigma对应的四个滤波核, 分别为a1, a2, b1, b2;
通过灰度图像与滤波核的卷积运算,得到四个处理后的图像imga1,imga2,imgb1, imgb2,显出角点位置, 抹平黑白平坦区;
平均图像: imgmu = (imga1 + imga2 + imgb1 + imgb2)/4;
在平坦区域, 经过四个卷积运算后, 值基本没什么变化, 但是在角点、边缘地方由于不同的构造滤波核,将使得边缘不同
方向的值不同,譬如a1核,将导致角点左上角边缘区明显大于其他核后的值,将该值减去平均图像, 就可以得到差值图;
通过不同sigma尺寸滤波核处理后的差值图即可以得到粗略的角点位置, 当然当前的角点还是一个斑点;
% template properties template_props = [0 pi/2 radius(1); pi/4 -pi/4 radius(1); 0 pi/2 radius(2); pi/4 -pi/4 radius(2); 0 pi/2 radius(3); pi/4 -pi/4 radius(3)]; disp('Filtering ...'); % filter image img_corners = zeros(size(img,1),size(img,2)); for template_class=1:size(template_props,1) % create correlation template template = createCorrelationPatch(template_props(template_class,1),template_props(template_class,2),template_props(template_class,3)); % filter image according with current template img_corners_a1 = conv2(img,template.a1,'same'); img_corners_a2 = conv2(img,template.a2,'same'); img_corners_b1 = conv2(img,template.b1,'same'); img_corners_b2 = conv2(img,template.b2,'same'); % compute mean img_corners_mu = (img_corners_a1+img_corners_a2+img_corners_b1+img_corners_b2)/4; % case 1: a=white, b=black img_corners_a = min(img_corners_a1-img_corners_mu,img_corners_a2-img_corners_mu); img_corners_b = min(img_corners_mu-img_corners_b1,img_corners_mu-img_corners_b2); img_corners_1 = min(img_corners_a,img_corners_b); % case 2: b=white, a=black img_corners_a = min(img_corners_mu-img_corners_a1,img_corners_mu-img_corners_a2); img_corners_b = min(img_corners_b1-img_corners_mu,img_corners_b2-img_corners_mu); img_corners_2 = min(img_corners_a,img_corners_b); % update corner map img_corners = max(img_corners,img_corners_1); img_corners = max(img_corners,img_corners_2); end
通过非极大抑制(NMS),我们可以在斑点中找到准确的位置(像素级);NMS一般用于搜索局部极大值;
2、亚像素级角点检测;
经过1处理后可以找到像素级的角点位置, 但是棋盘格一般用来标定, 最好是采用亚像素精度更好;
首先, 计算角点周围的边,得到边的方向v1, v2, 然后对3 * 3范围内的边缘点进行拟合计算求实际位置;
% non maximum suppression for i=n+1+margin:n+1:width-n-margin for j=n+1+margin:n+1:height-n-margin maxi = i; maxj = j; maxval = img(j,i); for i2=i:i+n //先找到一个象限一定区域内的极大值; for j2=j:j+n currval = img(j2,i2); if currval>maxval maxi = i2; maxj = j2; maxval = currval; end end end failed = 0; for i2=maxi-n:min(maxi+n,width-margin) // 然后,在这个极大值的邻域内找到比该极大值更大的; for j2=maxj-n:min(maxj+n,height-margin) currval = img(j2,i2); if currval>maxval && (i2<i || i2>i+n || j2<j || j2>j+n) failed = 1; break; end end if failed break; end end if maxval>=tau && ~failed maxima = [maxima; maxi maxj]; end end end
3、基于生长的检测;
经过1,2处理后, 角点的位置已经明确了, 下面就需要对所有的角点进行排布, 这就有问题了: 可能存在角点检测遗漏的情况。
首先, 通过一个焦点找到一个3 * 3的邻居角点阵列, 然后在通过外推(距离、方向),得到四个方向的理论位置,将该理论位置在剩下的
角点中找最近的点,同时计算当前的能量(判定函数)。理论上, 随着点的增多, 能 % for all seed corners do
for i=1:size(corners.p,1) % output if mod(i-1,100)==0 fprintf('%d/%d ',i,size(corners.p,1)); end % init 3x3 chessboard from seed i chessboard = initChessboard(corners,i); // 找到3 * 3 的邻居; % check if this is a useful initial guess if isempty(chessboard) || chessboardEnergy(chessboard,corners)>0 continue; end % try growing chessboard while 1 % compute current energy energy = chessboardEnergy(chessboard,corners); // 计算目前的能量; % compute proposals and energies for j=1:4 // 四个方向扩展; proposal{j} = growChessboard(chessboard,corners,j); //扩展, 生长; p_energy(j) = chessboardEnergy(proposal{j},corners); // 扩展后的能量; end % find best proposal [min_val,min_idx] = min(p_energy); % accept best proposal, if energy is reduced if p_energy(min_idx)<energy chessboard = proposal{min_idx}; if 0 figure, hold on, axis equal; chessboards{1} = chessboard; plotChessboards(chessboards,corners); keyboard; end % otherwise exit loop else break; end end % if chessboard has low energy (corresponding to high quality) if chessboardEnergy(chessboard,corners)<-10 //当能量小于-10; 因为最大-9 ( 3 * 3) % check if new chessboard proposal overlaps with existing chessboards overlap = zeros(length(chessboards),2); for j=1:length(chessboards) // 判断当前找的阵列是否与先前找的阵列有重叠区; for k=1:length(chessboards{j}(:)) if any(chessboards{j}(k)==chessboard(:)) overlap(j,1) = 1; overlap(j,2) = chessboardEnergy(chessboards{j},corners); break; end end end % add chessboard (and replace overlapping if neccessary) if ~any(overlap(:,1)) chessboards{end+1} = chessboard; else idx = find(overlap(:,1)==1); if ~any(overlap(idx,2)<=chessboardEnergy(chessboard,corners)) // 如果重叠区的能量比现有的阵列小, 那么久置换先前的; chessboards(idx) = []; chessboards{end+1} = chessboard; end end end end