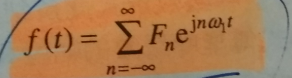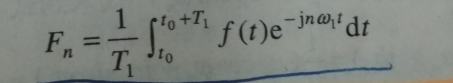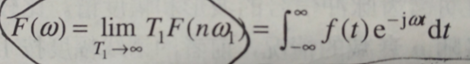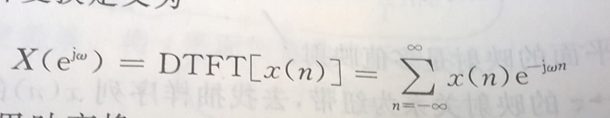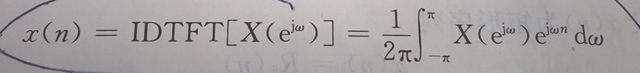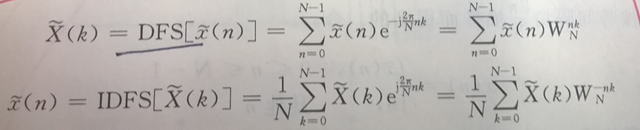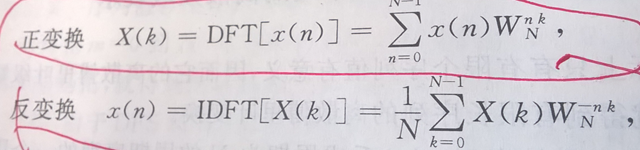学习了信号与系统及数字信号处理之后,什么感觉呢?这尼玛讲的什么玩意啊?数字数字信号处理考了62分哦。
这两天,又看了看,因为可能要用到的唉。
好像是这么回事:
我的理解吧,是这样的,对于各种变换无非就是通过数学公式把一个函数从一个域变到另一个域。变来变去发现它有点物理意义了呢,也或着奔着它的物理意义去的。
对于模拟信号:
1. 分解为傅里叶级数的情况:
信号是又时间 t 变化,并且为周期性的哦,这时,就可以把这个信号分解为一系列的正弦或余弦相叠加而成。(此时的频域上为离散的哦,因为这一系列正弦波的頻率为基頻的整数倍)。(可以看出:时域为周期的,频域而为离散的)
说明了:对于时间上为周期的,它的频域为离散的。
还想说明一点,当我们用指数形式表示傅里叶级数时,它的系数Fn与 F-n 一定是 共轭的哦,如果不是共轭,它就展不成三角函数的形式了,(对于这点,由于看了一本书上的一个例子的写错了,我纠结了不小一会,后来可以通过举例子得到)
变换公式:
要知道,复幅度 Fn 的模即为幅度谱、 而 Fn 的辐角主值(-pi, pi) 即为 相位谱啊; 而后面的 e jnwt 这个不用管,它的作用是与 Fn 相乘以后得到 f(t)的;
欧拉也太牛逼了吧,这么抽象的三角函数的欧拉公式他是怎么搞出来的!!!!!!!!
2. 分解为傅里叶变换的形式:
对于非周期信号,则分解为傅里叶变换的样子啦。因为吧,这时相当于周期为无穷大的周期信号,然后呢,它的基频相当于无穷小,所以就用连续的频域来进行变换,所以就有了傅里叶变换啦。它就相当于把信号分解为了分布在全部頻域上的一系列正弦信号相叠加。
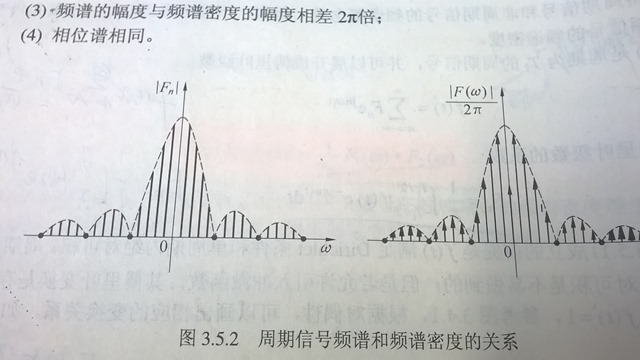
对于周期信号,如果你非要进行傅里中变换,也可以,但是要引用冲激函数,那么它的傅里叶变换由以前的一个个的散值变为了一个个离散的冲激函数。(看看下图就知道什么意思啦)
对于周期函数的一个周期内作傅里叶变换会怎么样呢??因为它不是周期的嘛,它的图像想想的话一定是连续的,因为它不是周期的嘛,它的样子就是(如果按如图上面的例子来的话)上图中的包络。 所以呢,周期信号呢,而在它一个周期内的信号的傅里叶变换上的图上的等间隔上取点。
变换公式:
周于什么拉普拉斯变换啦,Z变换啦,等,那玩意都是就是一个工具了。
深入理解上面的傅里叶级数与傅里叶变换的两个公式啊; 明白 频域的幅度与相位啊;
对于数字信号上:
它的特点就是信号为离散的,以 n 表示变量。 (而模拟信号中以 t 表示变量的哦,它是连续的,平时我们接触到的大多数信号都为连续的)。
首先说明的是,在表示频率的变量为:数字频率,什么意思呢?它就表示单位的间隔内信号变化了多少的rad( n 是离散的哦,所以为 一个 一个的点),相对比,在模似信号中的角频率, 它表示物理意义为:单位时间内(应该可以说1秒内)它变化了多少的rad.
看出了点什么没???? 因为在模似信号的横坐标为时间,所以用单位时间内; 而在数字信号中我们的横坐标为 n (一个一个的离散的点组成),所以我们用的为单位间隔。
1. 离散时间的傅里叶变换(就是一个个的无限长的小点点组成的数字信号):又叫做DTFT,定义的它的变换为这样的:
从上面你能看出什么??由于它在时间的变量为 n ,所以就出现了一个好玩的现象,频域信号为周期的;你这么想想,对于数字频率, 0.3pi 与 0.2pi + 2pi 有区别吗??答案为结果一样,这就是周期的了吧,即以2pi 为周期。为什么呢?一个间隔内 变化 2pi 的整数倍时,尽管两个端点中间的值在不断变化,但是别忘了,现在的离散的,而不是连续时间变化的,我们只关注在端的两个点处的变化,所以两个端点的值是不会变化的。
看看它的反变换:
看到了吧,只需要在一个周期内,我们就可以把信号从频域恢复到时间域上来,我们呢,对于我们有用的就是一个周期内的频域信号哦,谁让它是周期的来呢。
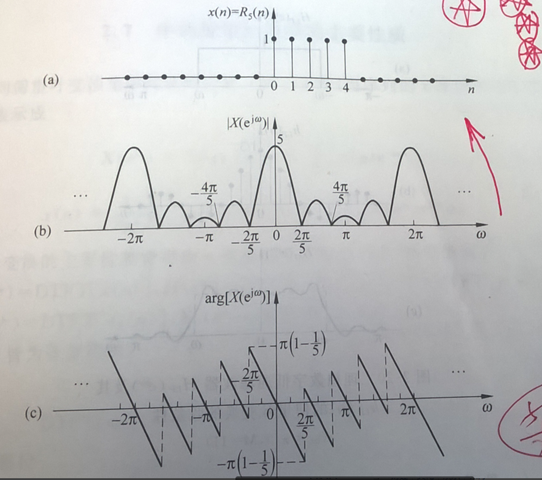
看一个例子:上面的图为时域,中间为频域上的幅度,下面为频域上的相位。
从另一个角度想它为什么是周期的: 上面已经说了,由于在一个间隔内,对于数字频率差为2pi * k 的, 可以看作是一样的。所以 呢,对于 在频域中,对于分量的数字频域为 w 的信号 幅度为A, 相位为B, 那么它也可以看作为是分量为 w + 2pi * k 的分量啊,且幅度与相位是相同的, 所以 这也就对应 了图上的频域为周期的形状。
对于这个变化,还说明一点为问题哦:对于时域为离散的,那么它的频域为周期的。
2,对于离散的周期的信号的离散的傅里叶级数(DFS):
这么说吧,从宏观上看,对于离散的时间信号,那么就对应频域为周期的吧(上面说明原因了), 对于周期的信号呢,它可以分解为离散的频域信号吧(可以从看模拟时间的傅里叶级数看出哦,或者说,因为为周期的,它的基频不是无穷小,所以呢,傅里叶级数分解为基频整数倍的一系列的信号,所以为离散啦)。 由于这样,所以呢,DFS的结果一定为离散且为周期的了。
这样就容易明白下面它的变化公式了:
也正如此,周期序列的傅里叶分解为有限个独立的谐波分量(大于N的时候它就重复了),有无论正反变换,它都是在周期为 N 上进行的。(我认为要先明白反变换,它就相当于把时域信号分解为频域信号, 具有物理意义吧。)
最后的结果:正反变换得到的时域与频域的序列都为周期为N的一个序列啦。
3, 离散的傅里叶变换(DFT):
对于有限长的离散频域表示时,做法就是把长度为N的有限长的序列看成周期为N的周期序列的一个周期,这样就用离散的傅里叶级数计算周期序列的一个周期啦。而频域看成原本周期序列的一个主值序列就可以啦。
所以呢,最终的变换公式为:
看到了吧,它和上面的傅里叶级数的分解变换公式没有什么区别,只是把无限的周期序列变为了限制在了有限的主序列了。
对于它,有一个FFT变换,FFT(快速傅里叶变换并不是一个新的变换,而是DFT的一种快速算法而已)。
上面讲的就是 时间——频域 之间变换方法的大致。 如果具体想看的话,当然需要看书上的详细内容。我只是大体在很宏观上说明了它们表示了什么意思,这样很容易理解的哦。
4. 离散余弦变换:
正变换:
反变换:
正变换与反变换的核是相同的,转置一下就可以了;
令正变换的核为A; F= A * X; (X 为一个一维的列信号, F为DCT变换的结果)
X = A的逆 * Y = A的转置 * Y ; 因为吧,这个A的每一列都是正交的,所以呢,转置就等于逆;
DCT变换的实质就是: 把一个信号表示成好多个余弦分量的叠加形式;