1、概述
神经网络一般是由多层网络结构组成,每层都是有感知器组成,各层之间的连接方式多种多样,如全连接。
前馈神经网络(feedforward neural network),简称前馈网络,是一种最简单的神经网络,也是目前应用范围最广泛、反正最迅速的一种神经网络。在此种神经网络中,各神经元从输入层开始,接收前一级输入,并输出到下一级,直至输出层。整个网络中无反馈,可用一个有向无环图表示。
前馈神经网络采用一种单向多层结构。其中每一层包含若干个神经元,同一层的神经元之间没有互相连接,层间信息的传送只沿一个方向进行。其中第一层称为输入层。最后一层为输出层.中间为隐含层,简称隐层。隐层可以是一层。也可以是多层。
2、感知器
感知器中最常用的是线性感知器,定义为:
$o(vec{w})=vec{w}cdot vec{x}$
对于一个感知器,其常用的误差定义为:
$E(vec{w})=frac{1}{2} sum_ {din D}(t_{d}-o_{d})^{2} $
其中D是训练样例集合,$o_{d}$是训练样例 d 的目标输出,$t_{d}$是线性单元对训练样例 d 的输出。$E(vec{w})$定为模型参数$vec{w}$的函数。
对一个感知器(神经单元),其直接的输入和输出(即该层激活函数的输入、输出)是标量。
3、模型训练-delta法则
3.1、delta法则核心思想
delta法则的核心法是使用梯度下降(gradient descent)来搜索可能权向量的假设空间,以找到最佳拟合训练样例的权向量。delta法则提供了反向传播算法的基础。
梯度下降搜索一个使E最小化的权向量是从一个任意的初始化权向量开始,然后沿误差曲面最陡峭下降的方向修改权向量,继续这个过程知道达到全局(或局部)的最小误差。其中误差曲面最陡峭下降的方向可由E相对$vec{w}$向量的各个分量求导获得,该向量导数即成为E对于$vec{w}$的梯度,记作$ riangledown E(vec{w}) $:
$ riangledown E(vec{w})=[frac{partial E}{partial w_0},frac{partial E}{partial w_1},cdots ,frac{partial E}{partial w_n}]$
$ riangledown E(vec{w}) $确定了使E最陡峭上升的方向,所以它的负方向就给出了最陡峭下降的方向,记$ riangle vec{w}$为:
$ riangle vec{w}=-eta riangledown E(vec{w}) $ (4.5)
这里$eta$为学习速率,值为正数。其中的负号是因为我们想要权向量向E下降的方向移动。
3.2、梯度分量的求导推导
梯度向量的分量$frac{partial E}{partial w_i}$的推导过程:
$frac{partial E}{partial w_i}=frac{partial}{partial w_i} frac{1}{2} sum_ {din D}(t_{d}-o_{d})^{2}$
$quad =frac{1}{2} sum_ {din D} 2 (t_{d}-o_{d}) frac{partial}{partial w_i} (t_{d}-o_{d})$
$quad =sum_ {din D} (t_{d}-o_{d}) frac{partial}{partial w_i} (t_{d}-vec{w}cdot vec{x_{d}})$
$quad =sum_ {din D}(t_{d}-o_{d}) (-{x_{id}})$ (4.6)
其中$x_{id}$表示训练样例d的一份输入分量$x_{i}$。
将等式(4.6)带入(4.5)得到梯度下降权值的更新法则:
$ riangle vec{w}=eta sum_ {din D}(t_{d}-o_{d}){x_{id}}$ (4.7)
4、激活函数
引入激活函数sigmoid,记此时的感知器成为sigmoid单元,其输出为:
$o=sigma (vec{w}cdot vec{x})$
其中$sigma (y) = frac{1}{1+e^{-y}}$ (4.12)。sigmoid函数一个有用特征是它的导数很容易用其本身表示:$frac{partial sigma (y)}{partial y}=sigma (y)cdot (1-sigma (y))$
5、模型训练-反向传播算法
前馈网络的反向传播算法-以包含两层sigmoid单元的网络为例。对于下图,包括隐藏层H和输出层O,对于输出层的每个神经单元,$net_{o}$表示未使用激活函数的输出,$out_{o}$表示使用激活函数后的输出,即:
$net_{o}=vec{w}cdot vec{x}$
$out_{o}=sigmoid(vec{w}cdot vec{x})$
同理对于隐藏层的每个神经单元,$net_{h}$表示未使用激活函数的输出,$out_{h}$表示使用激活函数后的输出。
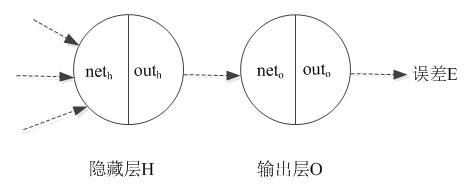
从单元$i$到单元$j$的输入表示为$x_{ij}$,单元$i$到单元$j$的权值表示为$w_{ji}$。
5.1、输出层单元权值更新
对于输出层的单元$o$,其权值更新值$frac{partial E}{partial w_{io}}$为 (这里$w_{io}$是表示隐藏层单元$i$到输出层单元$o$的权值):
$frac{partial E}{partial w_{io}}=frac{partial E}{partial out_o}cdot frac{partial out_o}{partial net_o}cdot frac{partial net_o}{partial w_{io}}$
计算$frac{partial E}{partial out_o}=frac{partial frac{1}{2} sum(target_{o}-out_{o})^{2}}{partial out_o}=-(target_{o}-out_{o})$
计算$frac{partial out_o}{partial net_o}=out_ocdot (1-out_o)$
计算$frac{partial net_o}{partial w_{io}}=x_{io}$
一般记$-frac{partial E}{partial out_o}cdot frac{partial out_o}{partial net_o}$为该输出单元的误差$delta_o$,有:
$delta_o=out_ocdot (1-out_o)cdot (target_{o}-out_{o})$
综上,$frac{partial E}{partial w_{io}}=-delta_ocdot x_{io}$,其反方向$-frac{partial E}{partial w_{io}}=delta_ocdot x_{io}$
即: $-frac{partial E}{partial w_{io}}=[x_{io}] cdot [out_ocdot (1-out_o)]cdot [(target_{o}-out_{o})] $
各部分(中括号内容)分别对应输出层的输入$x_{io}$、输出层状态到输出层输出的激活函数导数$out_ocdot (1-out_o)$、loss函数导数$(target_{o}-out_{o})$.
再考虑学习步长和冲量,那么输出单元o的权值$w_{ij}$的更新值:
$ riangle w_{io}(n)=eta delta_o x_{io} + alpha w_{io}(n-1)$
其中$eta$是学习步长,$alpha w_{io}(n-1)$是上一次迭代$w_{io}$的更新值。
5.2、隐藏层单元权值更新
对于隐含层的单元h,其权值更新值$frac{partial E}{partial w_{ih}}$为 (这里$w_{ih}$是表示输入层单元$i$到隐藏层单元$h$的权值):
$frac{partial E}{partial w_{ih}}=frac{partial E}{partial out_h}cdot frac{partial out_h}{partial net_h}cdot frac{partial net_h}{partial w_{ih}}$
计算$frac{partial E}{partial out_h}=sum_{oin outputs} frac{partial E_o}{partial out_h}$ 其中$outputs$是输出层神经单元集合,$o$为输出层的一个单元。
针对输出层单元$o$,计算$frac{partial E_o}{partial out_h}$
$quad =frac{partial E_o}{partial out_o}cdot frac{partial out_o}{partial net_o}cdotfrac{partial net_o}{partial out_h}$
$quad =delta_o cdotfrac{partial net_o}{partial out_h}$
$quad =delta_o cdot w_{ho}$ (注意这里的$w$的含义是隐藏层单元h到输出层单元o的权值,而不是输入层单元到隐藏层单元的权值,所以是$w_{ho}$)
因此,$frac{partial E}{partial out_h}=sum_{oin outputs}w_{ho} cdot delta_o$
计算$frac{partial out_h}{partial net_h}=(1-out_h)cdot out_h$
计算$frac{partial net_h}{partial w_{ih}}=x_{ih}$
同输出层,一般记$-frac{partial E}{partial out_h}cdot frac{partial out_h}{partial net_h}$为该隐藏单元的误差$delta_h$,有:
$delta_h=out_h cdot(1-out_h) cdot sum_{kin outputs}w_{ho} cdot delta_o$
即: $delta_h = [out_h cdot(1-out_h)] cdot [sum_{oin outputs}w_{ho}] cdot [out_ocdot (1-out_o)] cdot [(target_{o}-out_{o})] $
综上,$frac{partial E}{partial w_{ih}}=-delta_hcdot x_{ih}$,其反方向$-frac{partial E}{partial w_{ih}}=delta_hcdot x_{ih}$
即 $-frac{partial E}{partial w_{ih}} = [x_{ih}] cdot [out_h cdot(1-out_h)] cdot [sum_{oin outputs}w_{ho}] cdot [out_ocdot (1-out_o)] cdot [(target_{o}-out_{o})] $
各部分(中括号内容)分别对应隐藏层的输入$x_{ih}$、隐藏层状态到隐藏层输出的激活函数导数$frac{partial out_h}{partial net_h}$、隐藏层与下一层(输出层)的矩阵计算(wx+b): $frac{partial net_o}{partial out_h}$、输出层状态到输出层输出的激活函数导数: $frac{partial out_o}{partial net_o}$、输出层输出与loss函数的导数: $frac{partial E_o}{partial out_o}$
同输出单元一样,考虑学习步长和冲量,那么隐藏单元$h$的更新值$w_{ih}$:
$ riangle w_{ih}(n)=eta delta_h x_{ih} + alpha w_{ih}(n-1)$
其中$eta$是学习步长,$alpha w_{ih}(n-1)$是上一次迭代权值的更新值。
另:网络层之间的权重矩阵维度示意:
待: https://blog.csdn.net/u014038273/article/details/78289040
