神经网络与深度学习(更新至第6讲 循环神经网络)_哔哩哔哩_bilibili

注解:
1.几乎所有机器学习问题都可以以概率建模的角度考虑。
2.现在不是建立一个映射函数,而是建立x,y之间的条件概率关系式。
3.通常来说,机器学习中的标签值y是给定的,那怎么能看成是随机变量呢?
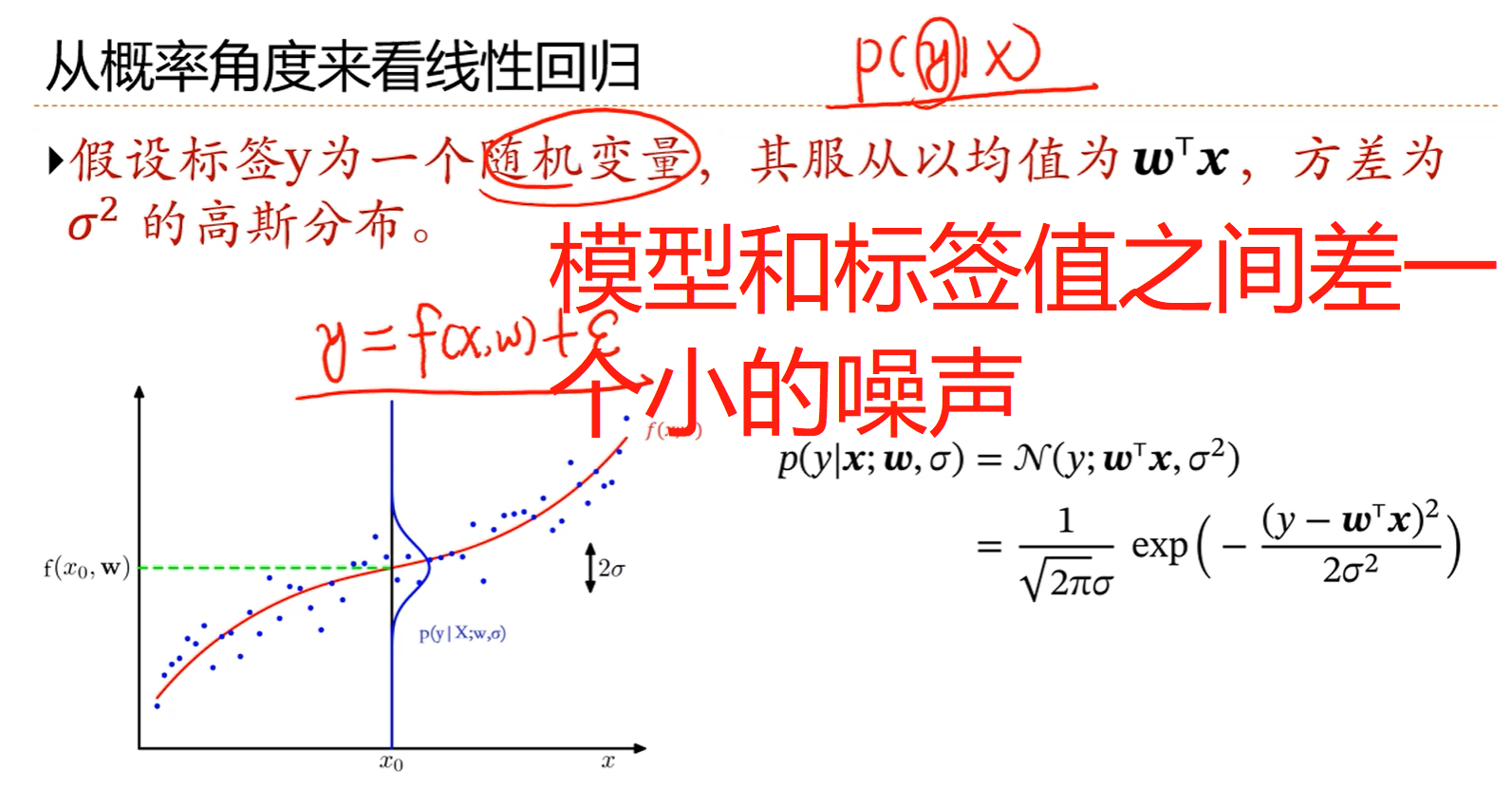
4.因为噪声ε~N(0,σ2)的高斯分布,所以:y~N(f(x,w), σ2),这样,y就是一个随机变量了。这里假设模型是解算出的线性回归模型:f(x,w)=wTx
5.从概率角度看线性回归实际上是站在一个更高的角度考虑问题,就是说在优化出了一个线性回归的模型之后,还要考虑一下优化的模型好不好,看看模型是否适用于新的样本,或者说模型在新样本上的误差ε的(分布)是一个怎样的情况。
6.条件概率的公式:
7.扩展知识点:线性回归-概率形式_哔哩哔哩_bilibili
线性回归的概率形式:

注解:
1.f(x,w)=wixi是一个一维或者多维的线性模型。
2.既然y服从高斯正态分布,那就一定有那个概率密度函数。
2.f(y)=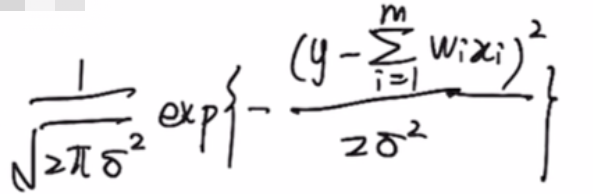

注解:
1.似然函数是:每个样本点出现的概率的连乘形式。
2.但连乘形式不好计算,所以似然函数的前面要加一个log。
3.y服从高斯分布的话,那y就应该看成是以一定的概率出现的,而不看成是确定的变量。
4.普通变量和随机变量的区别在于:普通变量是确定的值(比如y=f(x),一个确定的自变量x的值对应一个确定的变量y值),而随机变量则是以一定的概率出现的值。
5.假如y看成是一个随机变量了,那可能要用到极大似然估计的思想。(?)

注解:
1.把p(x;w)看成是x的函数;
2.把p(x;w)看成是w的函数;
3.机器学习中,通常要求的是w,所以应把p(x;w)看成是w的函数。

注解:
1.y是样本值。
2.X是样本的特征的值。
3.(X,y)构成了训练集。

注解:
1.在给定一个样本的特征的值X的情况下,它是正确标签的概率最大。这就是最大似然估计的目标。

注解:
1.加上log的原因:
a.机器学习里面,似然通常跟指数相关。大部分分布是指数族分布。
b.方便计算。
c.概率,特别是联合概率通常是比较小的值,会引起数值计算的问题。比如每个样本值的条件概率是0.01,那100个样本的联合概率就是:0.01100,这是一个很小很小的数值。
2.加上log后称为对数似然函数。

注解:
1.最大似然估计的解等价于最小二乘法的解,也即是等价于最小二乘里面的损失函数取最小值的解。

注解:
1.最大似然估计当中,y看成是一个随机变量的,参数w看成是一个参数,不是随机变量。有没有可能把w也看成是一个随机变量呢?答:有可能。这就是贝叶斯学习。此时,把原来对w的估计变成对w分布的估计。
2.w是在观测样本之后求解的分布,所以叫做后验分布。

注解:
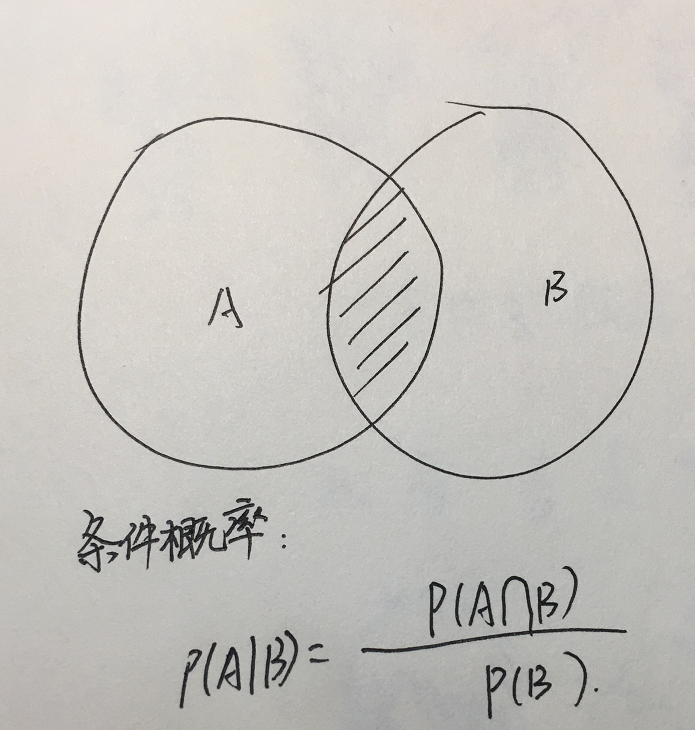
1.贝叶斯公式是用来说明两个条件概率之间关系的一个公式。
2.贝叶斯公式可以比较方便的对两个条件概率相互转换。
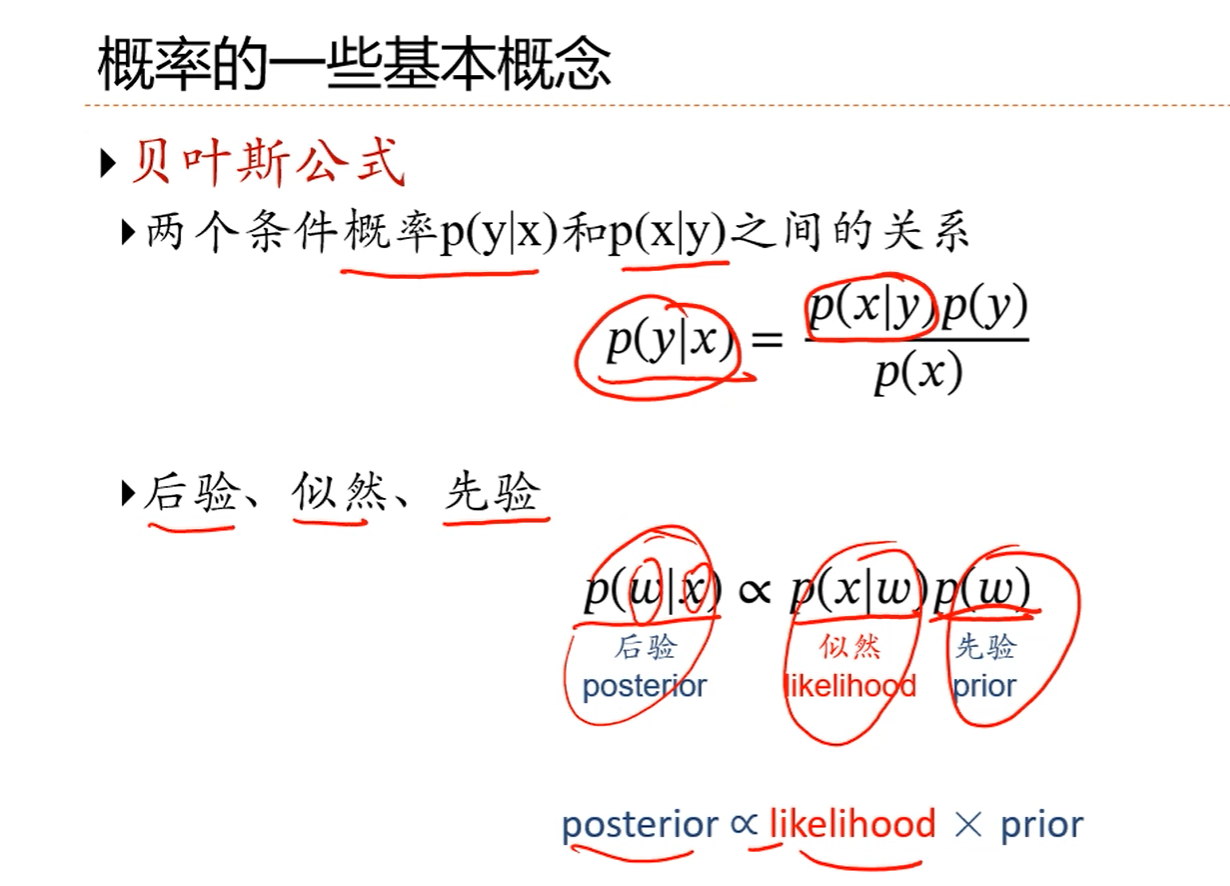
注解:
1.w看成是一个随机变量,x看成是样本观测值,p(w|x)就是一个后验概率,是关于参数w的后验分布。
2.p(w)不条件到任何观测上面,它称为先验。
3.符号是正比于。

注解:
1.w是一个分布,并没有一个值,所以还是没法用。
2.能做的事情是:给定后验分布w~p(w|x)的情况下,做出预测的期望。就是求一个期望。y=Ew~p(w|x...)[f(x,w)],这就是贝叶斯估计中如何利用随机参数w的分布的方法。这还是不方方便。
3.那怎么办?答:用点估计。

注解:
1.这个结果对应于带正则化系数的损失函数的优化。
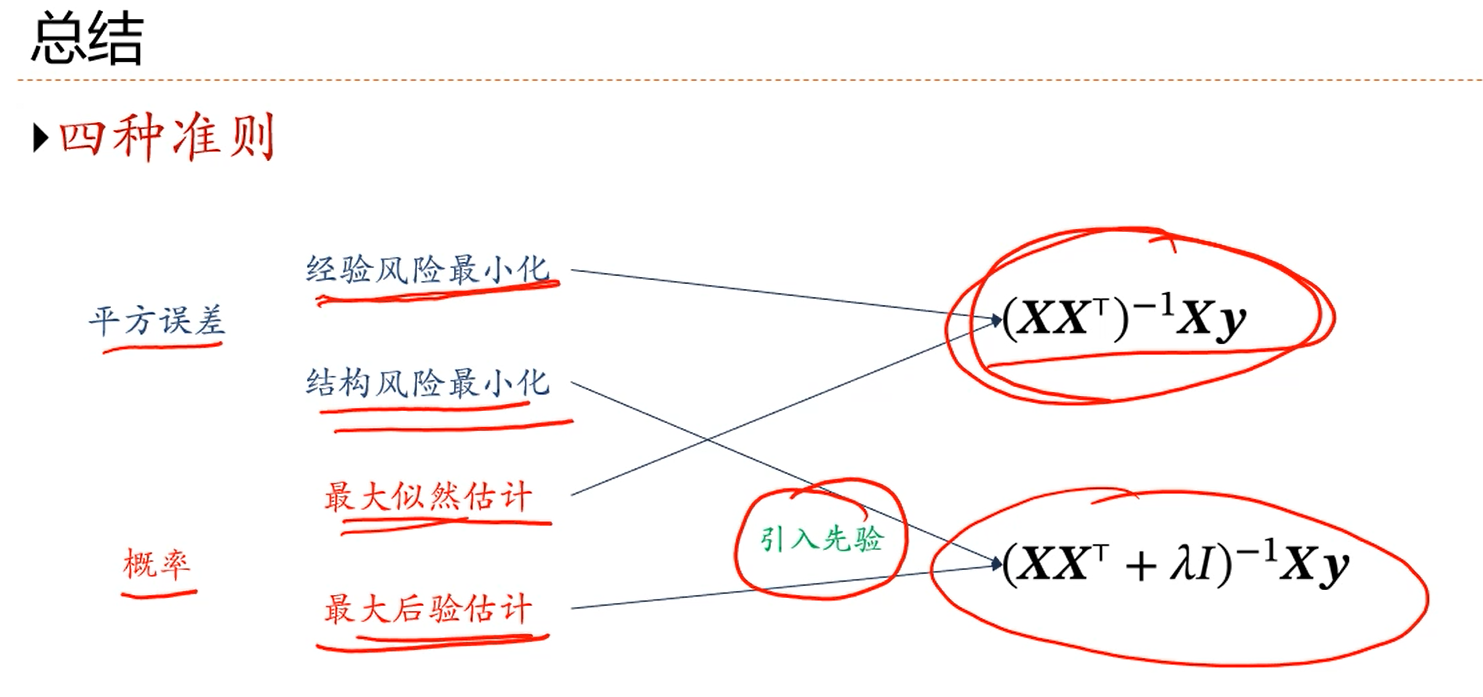
注解:
1.经验风险最小化的损失函数就是最小二乘准则下的一般的损失函数。
2.结构风险最小化就是在一般的损失函数形式的基础上加上一个防止过拟合(防止w参数很大)的正则化项(惩罚项)。
3.结构风险最小化里面引入的是正则化项。
4.最大后验估计里面引入的是关于p(w)的先验分布。
5.3和4都是引入了某种额外的知识。