http://bilibili.com/video/BV1Gf4y1S7e5?p=12&spm_id_from=pageDriver


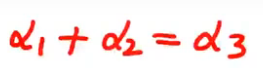
注解:
- 3向量可以由1向量和2向量表示。
把向量α1、α2、α3组成的矩阵(向量组)看成是一个方程组的系数矩阵。
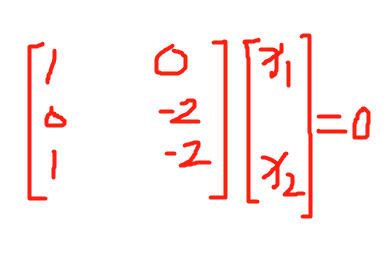


注解:
- 可以看出,方程3可以由方程1和2推得。
- 方程3是多余的方程,是假的方程,可以不要。
- 1、2可以组成最简方程组,这个最简方程组的系数矩阵中所包含的向量组就叫做极大线性无关组。

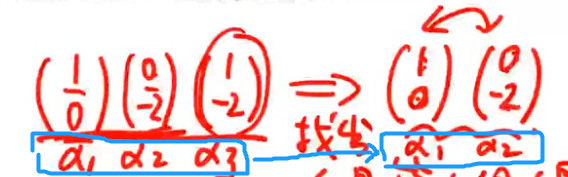


第2条的注解:
- 去掉的向量可以由最简向量组线性表示。
- 没有去掉的向量更加可以由最简向量组表示,因为没有去掉的向量组成了最简向量组,自己当然是可以由自己表示的。
- 综合以上两点,向量组中任一向量都可以由最简向量组表示。

注解:
- 则称向量组...是原向量组的一个极大线性无关组。

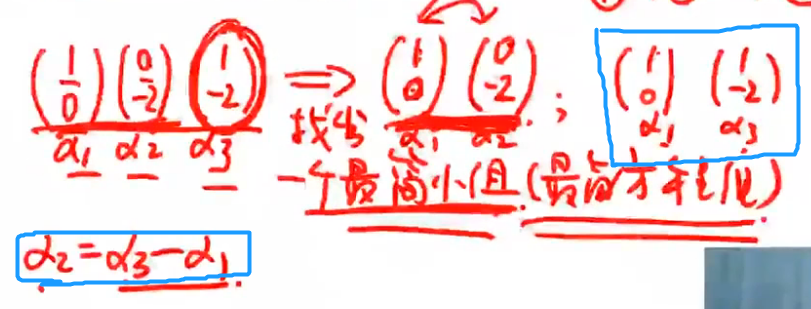
注解:
- 向量α1、α3也可以组成极大线性无关组。因为它们两个线性无关,这可以满足第一条。
- 向量α2可以由向量α1、α3线性表示,这可以满足第二条。
- 所以α1、α3可以组成一个极大线性无关组。


注解:
- 问题2和3以问题1为基础,1解出来了,2、3就知道了。

注解:
- 为何要做初等行变换,而不是做初等列变换?因为做初等行变换,相当于做方程组的同解变换。

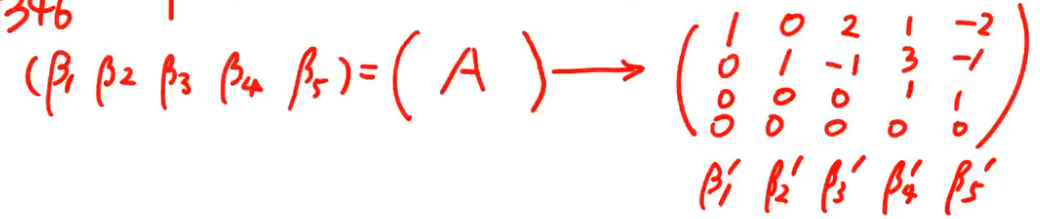

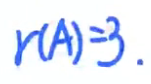


注解:
- 找到了一个极大线性无关组。但是人家要的是β向量组的极大线性无关组,不是β'的极大线性无关组。

注解:
- 互换两行,一行的k倍加到另一行,这些初等行变换不会改变方程组的解。
- 这个叫矩阵和方程组的同解变换。


注解:
- 经过初等行变换,虽然说矩阵很不一样了,但是其代表的方程组是同解方程组,未知量并没有发生任何的变化。
注解:
- 线性组合的系数没有发生变化,即方程组的解没有发生变化。


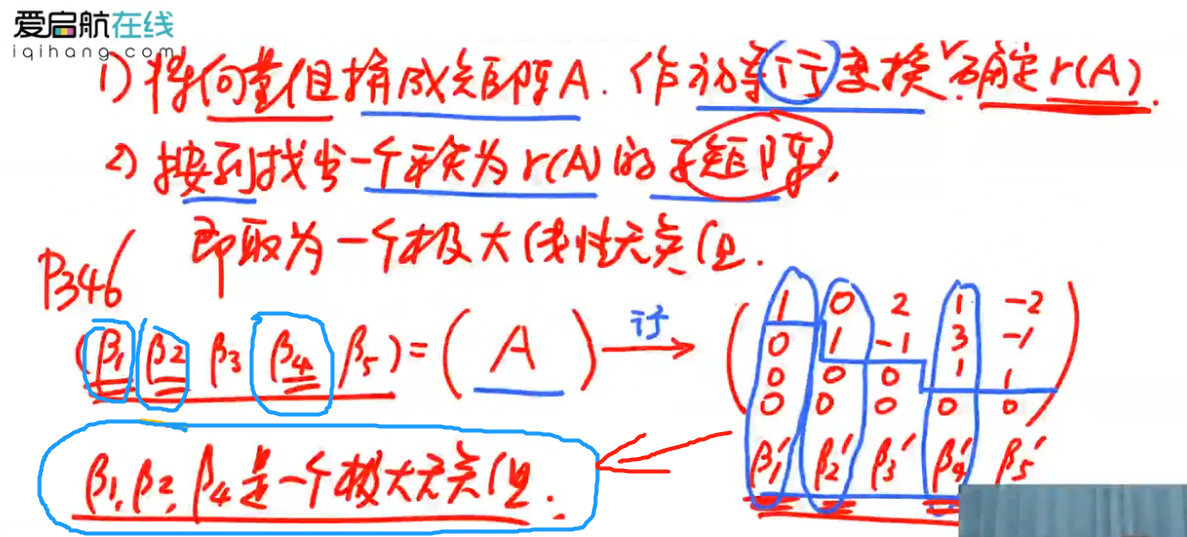
注解:
- 如果取了β1、β2、β4作为极大线性无关组,则意味着β3、β5可以由前者表示。
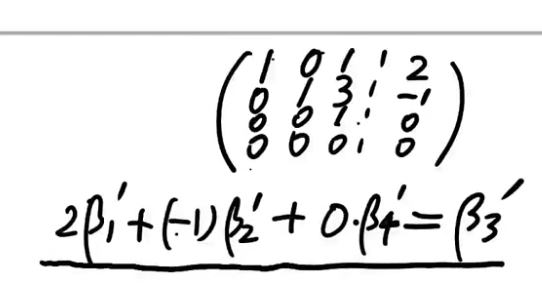
画成阶梯前后的矩阵或者说向量组具有相同的线性相关性,所以,一撇'可以去掉。
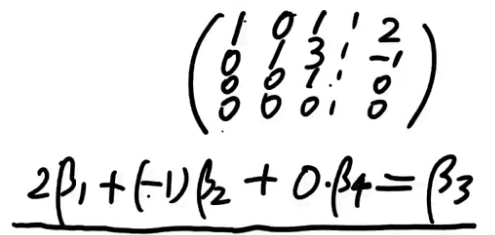
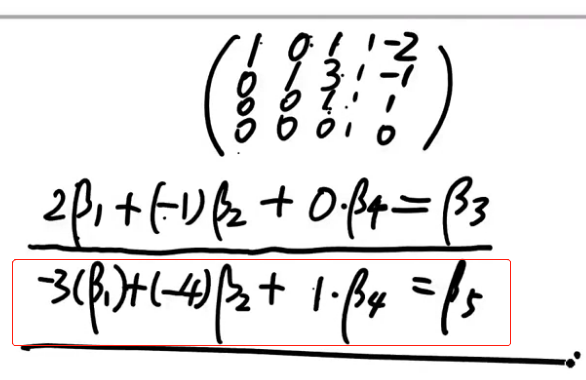


注解:
- 对于一个向量组(一个小组)内,有多余向量就会相关,无多余向量就是不相关,这是相关无关问题。
- 多余的向量可以由抽出来的无多余的那一组表示,这是线性表出的问题。
- 把多余的向量去掉,就得到了一个向量组的一个极大线性无关组。
- 任何一个小组都是可以由它的极大线性无关组表示的。
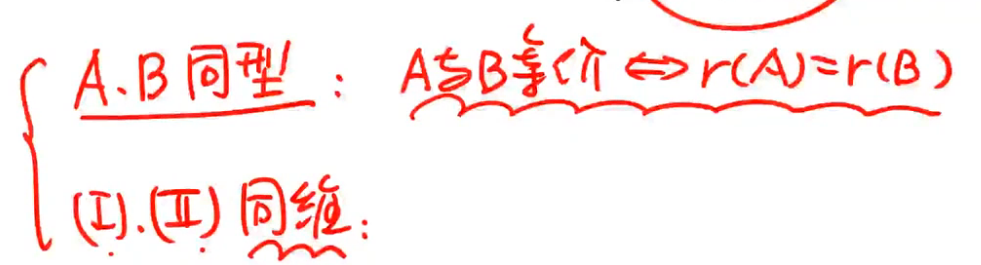



注解:
- A矩阵第1列第2列互换,然后第1行第2行互换,可以变成B矩阵;
- 什么叫矩阵等价?是指A矩阵能不能经过初等变换变成B矩阵。如果能经过初等变换变成B矩阵,就说明A、B矩阵等价。

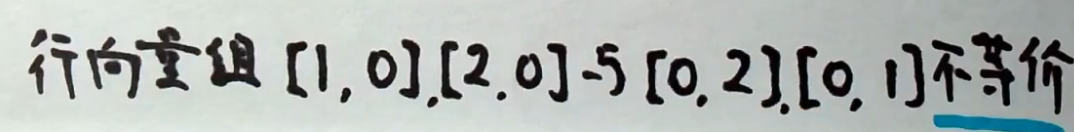
注解:
- 矩阵等价的时候,列向量组可以不等价;
- 矩阵等价的时候,列向量组不一定等价;
- 矩阵等价的时候,行向量组不一定等价;
- 矩阵的等价和向量组的等价是不同的概念。

注解:
- 矩阵等价,行向量组等价,列向量组等价。
- 列向量组可以相互线性表出。
- 行向量组可以相互线性表出。
- 矩阵等价是因为左边的矩阵可以经过两次初等变换变成右边的矩阵。

注解:
- 矩阵等价。
- 列向量组等价。
- 行向量组不等价。
小结:
- 两个矩阵而言,一个矩阵经过初等变换可以变成另一个矩阵,这叫矩阵等价。
- 两个向量组可以相互线性表出,这叫向量组等价。
- 矩阵等价和向量组等价是两个完全不同的概念。

注解:
- 秩表示向量组内极大线性无关组的个数。
- 也就是极大线性无关组的成员个数。
注解:
- 2是1的极大线性无关组,4是3的极大线性无关组。
- 2可以代表1,4可代表3.
- 1和2等价,3和4等价。
- 1、3的等价相当于2、4的等价。
- 1和3的单方表出可以转化成2和4的单方表出。
- 比方说,2可以由4单方表出。

注解:
- ζ1、ζ2...ζr可以由μ1、μ2...μr单方表出,则合起来的秩就是向量组μ1、μ2...μr的秩r。
- 既然ζ1、ζ2...ζr可以由μ1、μ2...μr单方表出,则前者是多余的向量(可以考虑齐次方程组)。

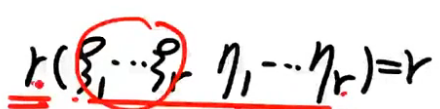
注解:
- 由于向量组ζ1、ζ2...ζr是多余的,所以拼起来的秩等于向量组μ1、μ2...μr的秩r。
- μ1、μ2...μr是极大无关组,向量组中向量的个数就是秩。
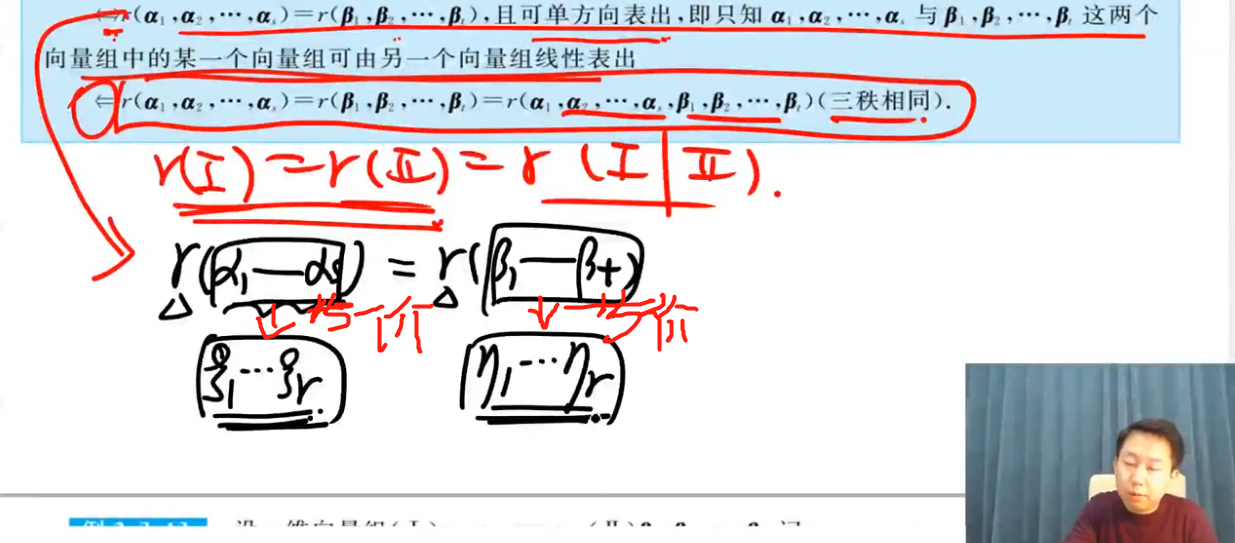
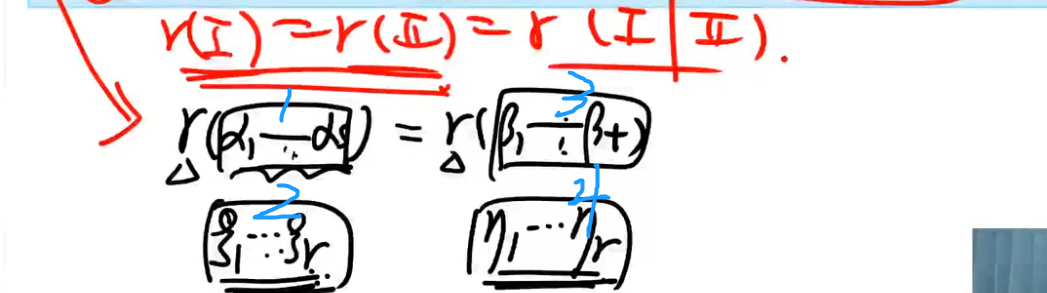
向量组ζ1、ζ2...ζr也是极大线性无关组,其秩也是向量组的个数r,它等于整体的秩r.站在ζ1、ζ2...ζr的角度考虑,μ1、μ2...μr是多余的向量组,所以μ1、μ2...μr也可以由向量组ζ1、ζ2...ζr表示了。所以,他们可以相互线性表示,2和4可以相互表示,意味着1和3也可以相互表示。于是,三秩相同。
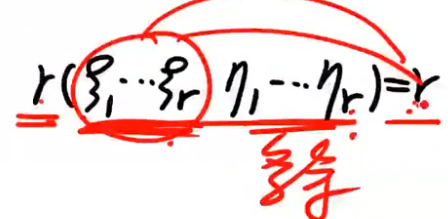
 (三秩相同)
(三秩相同)
注解
- 单方表出,相当于是被表出的那一方向ζ1、ζ2...ζr是多余的向量.
- 所以,对于两个向量组而言,三秩相等,必等价。等价,必有三秩相等。是充要条件。
习题:

注解:
- 求一个矩阵的秩的时候,可做行变换,也可做列变化,也可做行变换和列变换的混合变换。

注解:
- 求极大无关组的时候,只做初等行变换,因为这样才是相当于做方程组的同解变换。
第一问:


第二问: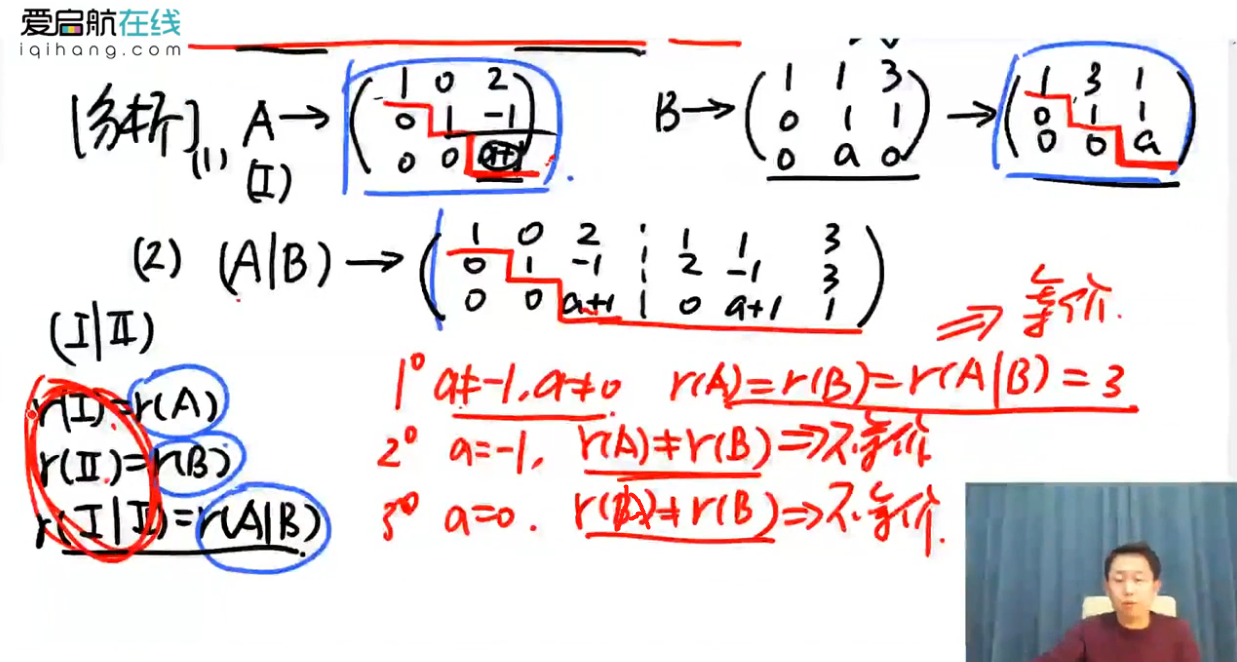
注解:
- r(A)=r(B),可以推出A矩阵和B矩阵等价。
- r(A)=r(B)=r(A|B),可以推出A矩阵所包含的向量组和B矩阵所包含的向量组等价。