引论

先定义一个permutation和另外一个permutation间的“距离”，（这里距离指从排列i到另一排列j所需的最小的合法操作数目，合法操作包括但不限于：交换任意两个不同位置的元素，交换任意两个相邻位置的元素，等等。如果从i到j的操作序列中的每个合法操作都有其对应的逆操作存在，(d(i,j)=d(j,i))）
permutation往深了说还是在研究(S_n)对称群，可以拿(改造过的)CayleyDiagram作为辅助理解

图片来自这个网站

总览

Ulam's distance这么理解也行

[operatorname{Ulam}(x, y)=|x|+|y|-2 cdot operatorname{lcs}(x, y) ]

Cayley distance

一般的两个排列间的距离

这里合法操作是交换任意两个不同位置的元素。

对于业余的爱好者而言只要知道红框这里面一段文字就行了，图片来自这篇论文

和全等排列间的距离

如果是求一个一般的n-排列(p)和全等排列之间的距离,答案就是 (n-[ ext{p的圆分解的圆个数}]) 。
感性的理解就是你要破环【元素数目>=2的圆】为【若干个不动点】，至少需要【元素数目-1】次操作，遍历所有的圆求和一下就得到了结果。

(*没有写异常处理*)
CayleyDistance[list_List, n_] := n - Length[PermutationCycles[list, head][[1]]]
CayleyDistance[{2, 5, 3, 6, 1, 8, 7, 9, 4, 10}, 10]

Kendall tau distance

一般的两个排列间的距离

也叫冒泡排序距离。这里合法操作是交换任意两个相邻位置的元素。
维基百科里给的定义式是

[Kleft( au_{1}, au_{2} ight)=left|left{(i, j): i<j,left( au_{1}(i)< au_{1}(j) wedge au_{2}(i)> au_{2}(j) ight) veeleft( au_{1}(i)> au_{1}(j) wedge au_{2}(i)< au_{2}(j) ight) ight} ight| ]

维基百科里给的例子如下

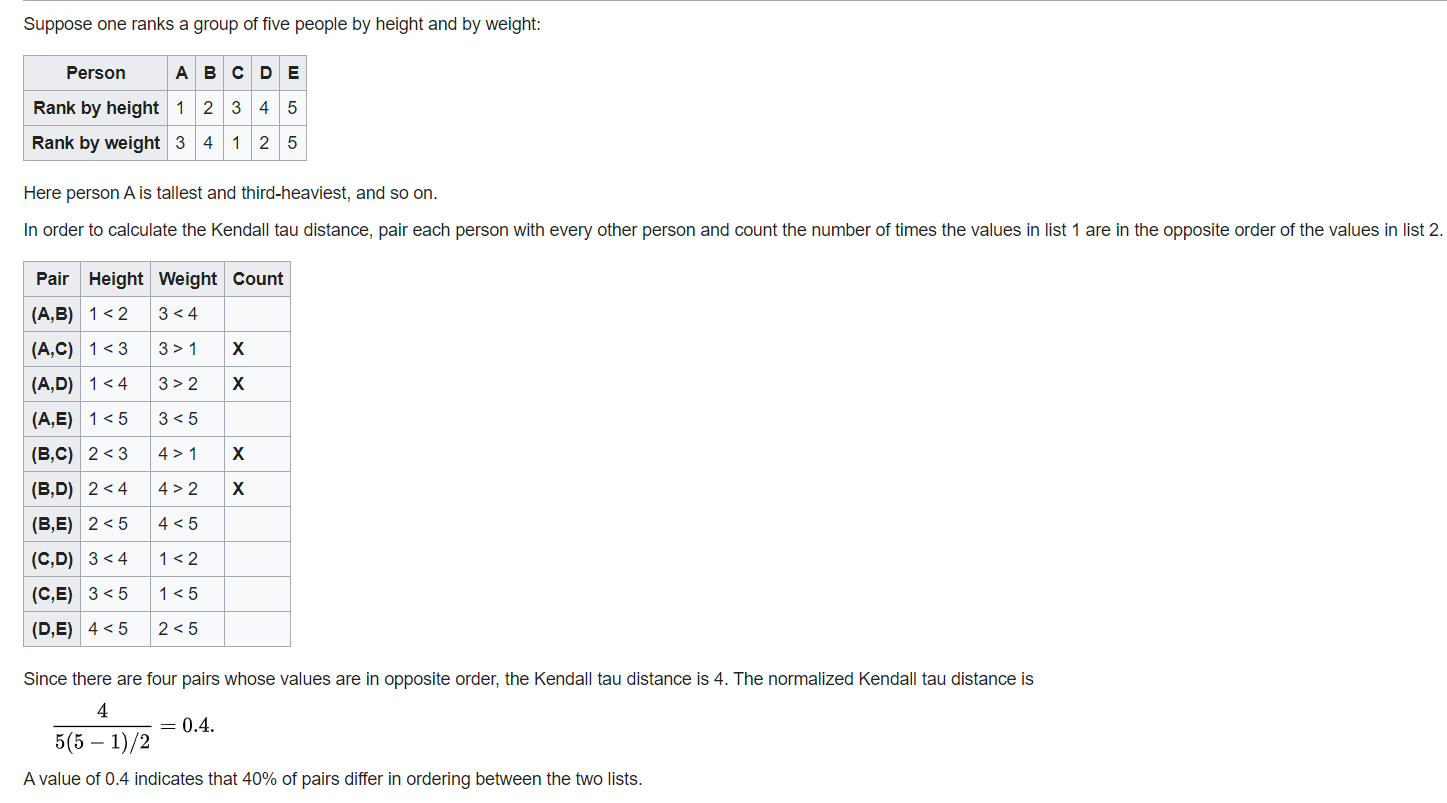
和全等排列间的距离

如果是求一个一般的排列(p)和全等排列之间的距离,答案就是(p)的逆序对数。证明？想象冒泡排序的那个过程，最开始的排列每有一个逆序对，相邻元素交换次数就加一。

#以下代码非本人编写

#方案1：冒泡排序并且计数:时间复杂度为O(n**2)，时间通不过
#方案2：参考优秀者的代码，使用包
#插入排序包
import bisect
while True:
    try:
        N=int(input().strip())
        a=[]
        for i in range(N):
            a.append(int(input().strip()))
        res=0
        lst=[a[0]]
        for i in range(1,N):
            j=bisect.bisect_left(lst,a[i])
            bisect.insort(lst,a[i])
            res+=i-j 
        print(res)
    except:
        break

参考

Complexity of Cayley Distance and other General Metrics on Permutation Groups
冒泡排序距离例题-排队唱歌_牛客题霸_牛客网
 StackOverflow帖子-Counting the adjacent swaps required to convert one permutation into another