来补一个小小的科技/cy
先咕着,切完eJOI再来填/doge
UPD 2020.7.23:前来填坑。u1s1 填坑是真心难受,以后争取不做鸽子(flag
定义
若一个回路经过一张图的每条边恰好一次,那么这个回路称为这张图的欧拉回路。
若一条起终点不同的路径经过一张图的每条边恰好一次,那么这条路径称为这张图的欧拉路。
无向图/有向图
无向图判定
- 若一张无向图连通,且所有点的度数都是偶数(可以理解为,沿某条没走过的边从任意一个点出来之后,一定可以延没走过的边回到这个点),那么它有欧拉回路,任意一个点都可以充当起终点;
- 若一张无向图连通,且恰有两个点的度数是奇数,其他点的度数都是偶数(偶点如上理解,奇点就是一个不进去了,一个不出来了),那么它有欧拉路,这两个奇点任意一个是起点,另一个是终点;
- 否则啥也没有。
有向图判定
- 若一张有向图的基图连通,且所有点的入度等于出度(同上),那么它有欧拉回路,任意一个点都可以充当起终点;
- 若一张有向图的基图连通,且恰有一个点的出度等于入度加一,一个点的入度等于出度加一,其他点的入度都等于出度(同上),那么它有欧拉路,起点是出度等于入度加一的点,终点是入度等于出度加一的点;
- 否则啥也没有。
求法
无向图/有向图的欧拉回路/欧拉路(一共四种情况)的求法是类似的。
首先按照上述判定找到起点,然后DFS。
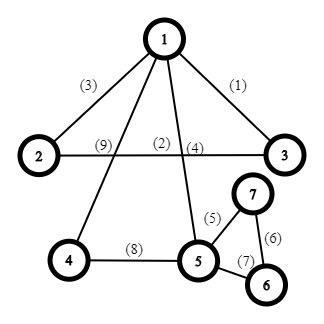
考虑从起点开始DFS。每到达一个节点,就选择连接当前点的任意一条未走过的边(对于有向图则是出边)(若没有则退出),将它标记成走过并沿它走出去,DFS到下一个节点,回溯时直接返回。也就是说在此节点只往外走一次,其他边不管了,反正其他边的话,将来会回到此节点继续走的。不过这是精神胜利法,反例还是能找出,比如下图,以无向图欧拉回路为例:

在上图中,已标号边的是已经走过的。从(1)开始,走到(5)的时候,它选择了走到(4)并回(1)而非走到(6/7)。这样一回去,哦吼,无路可走了。不难证明,遇到这样的情况后,把所有没走过的边,带着所有连接的点给抽出来得到一张子图,这个子图一定有欧拉回路/欧拉路(你要求啥就有啥)。假设我们已经找到了这个子图的欧拉回路/欧拉路,那么剩下来的事情就是将当前环和子图的欧拉路/欧拉回路合并起来。很显然,将子图的欧拉路/欧拉回路在连接处嵌入当前环是一种合并方法,如下图:
具体嵌入方法是:每次DFS回溯的时候不立即返回,取而代之的是将“将此边信息压入欧拉回路/欧拉路序列(即要求的东西)”这个操作放到回溯的时候完成,并继续找下一条邻接表中的未走过的边。这样最后欧拉回路/欧拉路序列是倒序的,reverse一下即可。正确性很好理解,进入子图之前显然是回溯回来的,此时已将所有在子图之后走过的边压入,紧接着就将子图压入,再按环的顺序倒退回去,将在子图之前走过的边压入。
最后说一句,我们可以类似网络流里的当前弧优化(我知道这个是因为以前学过网络流,现在忘掉内容了,只记得这个名字),实时记录当前走到当前点邻接表中的哪条边了。另外,对于无向图中的删边,我们要将邻居邻接表中连向自己的边也一并标记掉,我们可以预先开跟邻接表大小相等的反边vector。至于链式前向星,个人不喜欢那东西。
时间线性。
下面是简短的代码:
vector<edge> pa;//edge是存储边信息的类型
void dfs(int x=st){//st为找出的起点
for(int &i=now[x];i<nei[x].size();i++)if(!ban[x][i]){//未走过
int y=nei[x][i];
ban[x][i]=ban[y][reg[x][i]]=true;//标记
dfs(y);
pa.pb(edge(x,y));//压入
}
}
例题
CodeForces 1361C - Johnny and Megan's Necklace
洛谷 P6305 - 循环排序
混合图
这个听说要网络流/jk,暂时不会,留坑,嗷嗷待补。