一、最大流问题
问题表述:给定一幅图(n个结点,m条边),每一条边有一个容量,现在需要将一些物品从结点s(称为源点)运送到结点t(称为汇点),可以从其他结点中转,求最大的运送量。
在介绍最大流问题的解决方法之前,先介绍几个概念:反向弧,残余网络,增广路径,最大流定理。
反向弧:
若从 u 到 v 的边的容量为 c ,这条边上有流量 f 流过(称为正向弧),则相当于从 v 到 u 有一条容量为 0 的边,其流量为 - f ,这条边就是反向弧 。
反向弧的意义:反向弧的作用是起到有更优决策的时候会使当前选择的弧会自动放弃。反向弧有流量的原因是因为如果刚刚选择了正向弧,下一次如果存在更优策略使这 f 的流量流入汇点,就可以选择反向弧,将流量 f 撤销。
残余网络:
计算出图中的每条边上容量与流量之差(称为残余容量),即可得到残余网络。注意由于反向边的存在,残余网络中的边数可能到达原图中边数的两倍。
举例如下:
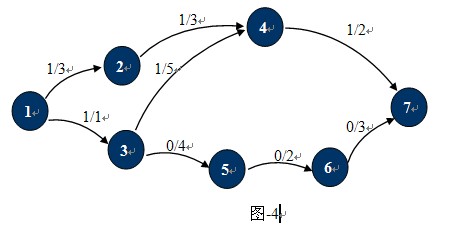
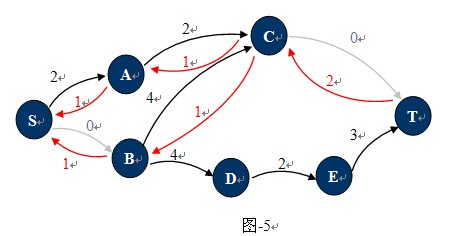
观察图-4,这种状态下它的残余网络如图-5所示:
增广路径:
残余网络中任何一条从 s 到 t 的有向道路都对应一条原图中的增广路径 —— 只要求出该道路中所有残量的最小值 d ,把对应的所有边上的流量增加 d 即可,这个过程称为增广。
最大流定理:
如果残留网络上找不到增广路径,则当前流为最大流;反之,如果当前流不为最大流,则一定有增广路径。
这样的话,求解最大流就只需要在残余网络中寻找增广路,直到不存在可以从 s 流向 t 的增广路,此时即为最大流。
求解最大流问题的高效算法有 dinic , sap 和 isap ,具体请看模板。
二、最小割最大流定理
割:
将原图中所有顶点分成两个集合 S 和 T = V - S ,其中源点 s 在集合 S 中,汇点 t 在集合 T 中。如果把 ” 起点在 S 中,终点在 T 中 “ 的边全部删除,就无法从 s 到达 t 了。这样的集合划分(S,T)称为一个割,它的容量定义为:∑(边( u , v )的容量和),其中 u ∈ S , v ∈ T ,即起点在 S 中,终点在 T 中的所有边的容量和。(这里所有的边都不包括反向弧)
最小割:
图中所有的割中,边权值和最小的割为最小割。
最小割最大流定理:
最大流的值为最小割的容量!
如何求最小割:
求完最大流后,在残留网络中从源点 s 开始 dfs ,将能到达的点标号( c - f >0 的边),已标号结点的集合为S,未标号结点集合为 T,则边集[ S , T ]为最小割。
定理证明:参见刘汝佳的《算法竞赛入门经典(第二版)》(紫书)第 370 页,如下:
从s运送到t的物品必然通过跨越S和T的边,所以从s到t的净流量等于|f|=f(S,T)=∑f(u,v)≤∑c(u,v)=c(S,T)。(u∈S, v∈T)
注意这里的割(S,T)是任取的,因此得到了一个重要的结论:对于任意s-t流和任意s-t割(S,T),有|f|≤c(S,T)。
下面来看残余网络中没有增广路的情形。既然不存在增广路,在残余网络中s和t并不连通。当BFS没有找到任何s-t道路,把已标号结点集合看成S,令T=V-S,则在残余网络中S和T分离,因此在原图中跨越S和T的所有弧满载(这样的边才不会存在于残余网络中),且没有从T回到S的流量,因此|f|= c(S,T)成立。
前面说过,对于任意的f和(S,T),都有|f|≤c(S,T),而此处又找到了一组让等号成立的f和(S,T)。这样便证明了最小割最大流定理。
三、最小费用最大流问题
问题描述:假设每条边除了有一个容量限制外,还有一个单位流量所需的费用(cost)。求在总流量最大的前提下,总费用最小的流,即最小费用最大流。
算法:与最大流算法类似,但每次用最短路 spfa 算法而非 bfs 找增广路。只要初始流是该流量下的最小费用可行流,每次增广后的新流都是新流量下的最小费用流。另外,费用值是可正可负的。具体实现方法请看模板。

