散点图
曲线直线化:变量变换后拟合线性模型、曲线拟合模型
非线性模型
残差的独立性、正态性、方差齐性检验
预测值
1、案例背景
利用某车企过去14年的汽车销售量来预测未来2-3年的销售量。变量:时间、销售量
2、数据理解
画时间与销售量的散点图,发现以下三类关键信息:
变量间是否存在数量关联趋势;
如果存在,是线性还是非线性;
是否存在明显的偏离点,是否可能成为建模时的强影响点。

通过观察散点图发现,需要删除1988-1992年的数据;需要把年1993-2001转化为1-9数字。
写代码或通过“转换-计算变量-选择个案”步骤得到。
3、变量变换后的线性回归
线性回归模型简介:
线性回归模型基本结构
yi=yiˆ+ei 即测量值=估计值+残差。估计值是通过模型获得的因变量的平均取值。
由于残差的存在,如何得到最优的拟合模型,一般采用最小二乘法来拟合模型,即保证各实测点至回归直线纵向距离的平方和最小。即∑ei2=min
常用指标
偏回归系数:即bi,表示自变量xi对因变量的影响程度。简称回归系数;
标化偏回归系数:将各自变量进行标准正态变换后建立回归模型得到的系数。用于比较各自变量对因变量的影响程度。
决定系数:相应的相关系数的平方。R2,反映因变量的全部变异中能够通过回归关系被自变量解释的比例,即自变量所能解释的方差在总方差中所占的比例。调整后的决定系数主要用于对自变量数量不同的模型拟合效果进行对比。
回归模型的适用条件
自变量与因变量是线性关系;
独立性:因变量相关独立,即残差相互独立;
正态性:因变量服从正态分布,即残差服从正态分布;
方差齐性:因变量的方差相同,即残差的方差相同。
变量变换后拟合线性回归模型:
销量与时间是非线性的,预拟合二次方曲线。所用变量:销量,时间,时间平方,建立线性关联。

模型拟合效果的判断:(检验残差的独立性、方差齐性)
残差独立性检验有以下三种方法:DW检验、绘画残差分布图、绘制残差时序图。分别如下:
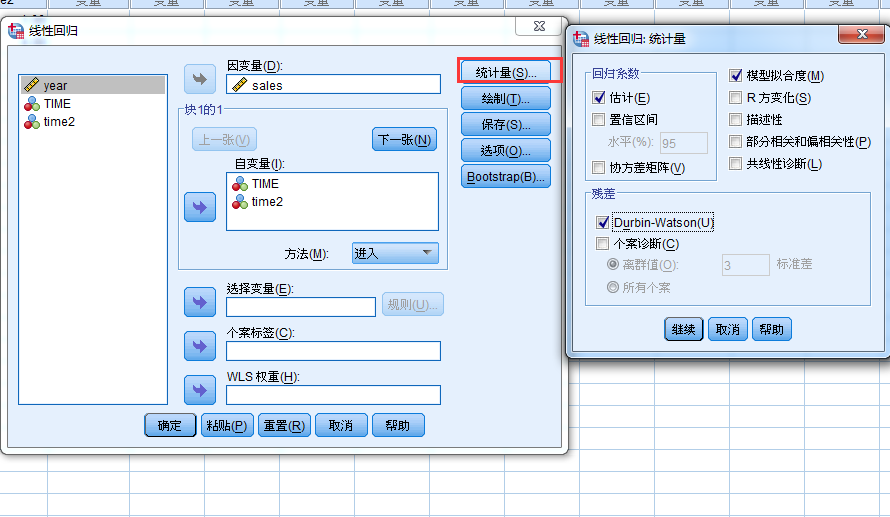
第三种方法:绘制残差时序图,首先保存标准化残差,接下来在“分析-预测-时序图”中画残差的时序图。


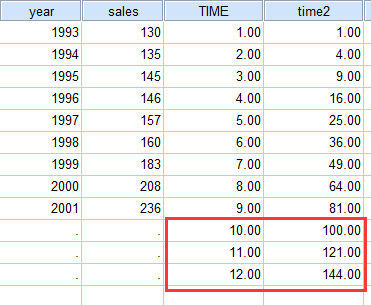
存储预测值和区间估计值:
由于是预测未来2-3年的销售量,所以先在time中新增三条记录,再进行回归分析,在保存中选中预测值。

4、曲线拟合
用曲线估计过程同时拟合多个曲线模型:

模型拟合效果判断:
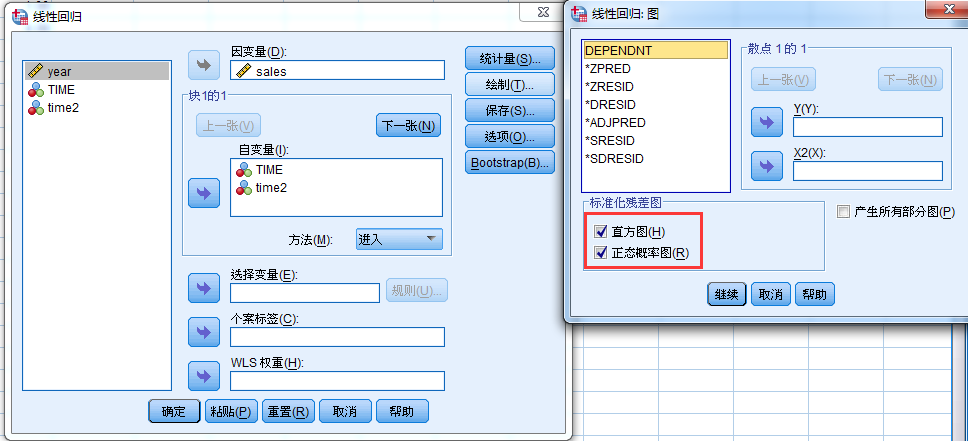
绘制残差的时序图检验残差的独立性即自相关性,其他检验相关性的方法?;绘制残差的P-P图检验残差的正态性。
模型的预测:
同第三节的预测。
5、利用非线性回归进行拟合
变量变换后的线性回归和曲线拟合都是采用曲线直线化的策略,这样的策略可能会使建立的模型不是最优或者根本找不到合适的曲线表达式。这时候,需要建立非线性回归。
非线性回归模型的一般形式:
yi=f(x,θ)+ei
非线性模型估计参数的思想类似于线性模型,即使残差平方和=min的参数估计值,只是此时的模型回归线是曲线。
构建分段回归模型:

注意:
回归结果中:参数估计值的标准误为近似标准误,所以相应的可信区间仅供参考,所有输出结果不给出参数的检验结果。
ANOVA方差分析结果中,由于是非线性回归,所以结果不给出方差分析的F值和P值。
不同模型效果的比较:
将三次方模型和分段回归模型的预测值,在“分析-预测-时序图”中进行对比。