时域
直观的从坐标上说,其横轴为时间,纵轴为对应函数量,其反应的是函数关于时间的一个变化过程。其往往有一个信号处理的背景,函数量即为信号在某一时间的值。
频域
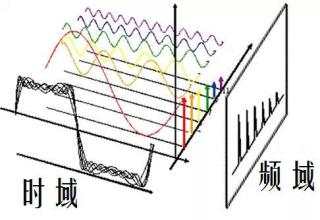
频域的横坐标是频率,纵坐标是相关函数的幅度,对应函数便与周期性有一定的关系了。频域是一种数学工具,描述了一个函数或者说信号中包含的成分,这些成分主要由频率与幅度来描述。正弦波是频域中唯一存在的波形,是用于描述的基本量。这样在时域中复杂的数据在频域中就变的老老实实。
例如
s
i
n
4
π
x
sin4pi x
sin4πx幅度为1,周期为
1
2
frac{1}{2}
21,频率为2,在频域中就是对应(2,1)。
含义
傅里叶变化是一种将函数信号由时域转换到频域的工具,其将满足一定条件的函数进行转换,变为一系列三角函数(正弦/余弦函数),或其积分(一般积分完了还是三角函数的形式)的线性组合。由于三角函数可以由sinx进行描述,所以可以在频域图对应,于是就完成了一个由时域往频域变换的过程,或者说是一个特征的提取。
级数
通过含义的理解,我们发现其与傅里叶级数的描述类似,也是将一个函数表示为三角函数形式,所以以傅里叶级数开始,对于一个周期为
2
l
2l
2l的函数且满足狄里赫利条件有:
f
(
x
)
=
a
0
+
∑
n
=
1
∞
(
a
n
c
o
s
n
π
x
l
+
b
n
s
i
n
n
π
x
l
)
f(x)=a_0+sum^{infty}_{n=1}(a_ncosfrac{npi x}{l}+b_nsinfrac{npi x}{l})
f(x)=a0+∑n=1∞(ancoslnπx+bnsinlnπx)
为了便于理解,我们将其中
π
l
=
w
frac{pi}{l}=w
lπ=w,
2
π
w
frac{2pi}{w}
w2π为周期,频率为
1
2
l
frac{1}{2l}
2l1,
w
w
w与频率之间只差一个系数,于是有:
f
(
x
)
=
a
0
+
∑
n
=
1
∞
(
a
n
c
o
s
n
w
x
+
b
n
s
i
n
n
w
x
)
f(x)=a_0+sum^{infty}_{n=1}(a_ncosnwx+b_nsinnwx)
f(x)=a0+∑n=1∞(ancosnwx+bnsinnwx)
转换一下可以得到其复指数形式:
f
(
x
)
=
∑
n
=
−
∞
n
=
∞
(
c
n
e
i
n
w
x
)
f(x)=sum^{n=infty}_{n=-infty}(c_ne^{inwx})
f(x)=∑n=−∞n=∞(cneinwx)
c
n
c_n
cn有
c
0
=
a
0
c_0=a_0
c0=a0,
c
n
=
a
n
−
i
b
n
2
c_n=frac{a_n-ib_n}{2}
cn=2an−ibn,n取整数。
正交
三角函数有正交的性质,对应的由欧拉公式我们对于复指数也有相似的性质,对于
e
i
n
w
x
e^{inwx}
einwx进行乘积与积分运算,同样为了方便运算取
w
=
1
w=1
w=1。
对于
∫
−
π
π
e
i
n
w
x
e
i
m
w
x
d
x
int^pi_{-pi}e^{inwx}e^{imwx}dx
∫−ππeinwxeimwxdx,变换一下有
∫
−
π
π
e
i
(
n
+
m
)
x
d
x
int^pi_{-pi}e^{i(n+m)x}dx
∫−ππei(n+m)xdx(m不等于n且均为整数)
再对应欧拉公式
e
i
x
=
c
o
s
x
+
i
s
i
n
x
e^{ix}=cosx+isinx
eix=cosx+isinx得:
∫
−
π
π
c
o
s
(
n
+
m
)
x
+
i
s
i
n
(
n
+
m
)
x
d
x
=
0
int^pi_{-pi}cos(n+m)x+isin(n+m)xdx=0
∫−ππcos(n+m)x+isin(n+m)xdx=0
特殊的n与m相等,但不为0有
∫
−
π
π
c
o
s
2
n
x
+
i
s
i
n
2
n
x
d
x
=
0
int^pi_{-pi}cos2nx+isin2nxdx=0
∫−ππcos2nx+isin2nxdx=0
所以我们得到了与三角函数相似的关于复指数积分的正交性。
变换
继续处理上面的
f
(
x
)
=
∑
n
=
−
∞
n
=
∞
(
c
n
e
i
n
w
x
)
f(x)=sum^{n=infty}_{n=-infty}(c_ne^{inwx})
f(x)=∑n=−∞n=∞(cneinwx),对两边进行乘积与积分有:
∫
−
l
l
f
(
x
)
c
n
e
−
i
n
w
x
d
x
=
∫
−
l
l
∑
n
=
−
∞
n
=
∞
(
c
n
e
i
n
w
x
)
e
−
i
n
w
x
d
x
int^l_{-l}f(x)c_ne^{-inwx}dx=int^l_{-l}sum^{n=infty}_{n=-infty}(c_ne^{inwx})e^{-inwx}dx
∫−llf(x)cne−inwxdx=∫−ll∑n=−∞n=∞(cneinwx)e−inwxdx
于是有正交性得到:
∫
−
l
l
f
(
x
)
e
−
i
n
w
x
d
x
=
∫
−
l
l
c
n
d
x
=
2
l
c
n
int^l_{-l}f(x)e^{-inwx}dx=int^l_{-l}c_ndx=2lc_n
∫−llf(x)e−inwxdx=∫−llcndx=2lcn(这里的
c
n
c_n
cn为一个复数)
将
c
n
c_n
cn提出来有
c
n
=
1
2
l
∫
−
l
l
f
(
x
)
e
−
i
n
w
x
d
x
c_n=frac{1}{2l}int^l_{-l}f(x)e^{-inwx}dx
cn=2l1∫−llf(x)e−inwxdx,这里的
2
l
2l
2l也就是周期T。
这里为啥把 c n c_n cn单独提出来,是因为对于 f ( x ) = ∑ n = − ∞ n = ∞ ( c n e i n w x ) f(x)=sum^{n=infty}_{n=-infty}(c_ne^{inwx}) f(x)=∑n=−∞n=∞(cneinwx),在周期确定的时候,具体决定 f ( x ) f(x) f(x)的是 c n c_n cn, e i n w x e^{inwx} einwx在周期已知的情况下与 f ( x ) f(x) f(x)之间并没有太大关系。并且通过不同的 n n n确定的频率与对应的 c n c_n cn就是频域的上的数据了。
周期
在傅里叶级数中,考虑的是周期函数的展开,对于一般函数时,也就是将周期进行一个无穷的极限逼近,于是原先的
2
l
2l
2l也就是T会趋于无穷,就得到了一般性的定义。这时的
f
(
x
)
=
∑
n
=
−
∞
n
=
∞
(
c
n
e
i
n
w
x
)
f(x)=sum^{n=infty}_{n=-infty}(c_ne^{inwx})
f(x)=∑n=−∞n=∞(cneinwx),并且之前有
2
π
w
=
2
l
=
T
frac{2pi}{w}=2l=T
w2π=2l=T,于是
w
w
w趋于0。
于是带入一下有
f
(
x
)
=
lim
w
−
>
0
∑
n
=
−
∞
n
=
∞
(
w
2
π
∫
−
∞
∞
f
(
x
)
e
−
i
n
w
x
d
x
e
i
n
w
x
)
f(x)=limlimits_{w->0}sum^{n=infty}_{n=-infty}(frac{w}{2pi}int^infty_{-infty}f(x)e^{-inwx}dxe^{inwx})
f(x)=w−>0lim∑n=−∞n=∞(2πw∫−∞∞f(x)e−inwxdxeinwx),进一步将
w
w
w换成
d
w
dw
dw,离散的求和在极限下成为积分有:
f
(
x
)
=
∫
−
∞
∞
1
2
π
∫
−
∞
∞
f
(
x
)
e
−
i
n
w
x
d
x
e
i
n
w
x
d
w
f(x)=int^infty_{-infty}frac{1}{2pi}int^infty_{-infty}f(x)e^{-inwx}dxe^{inwx}dw
f(x)=∫−∞∞2π1∫−∞∞f(x)e−inwxdxeinwxdw。
形式
f
(
x
)
=
1
2
π
∫
−
∞
∞
∫
−
∞
∞
f
(
x
)
e
−
i
n
w
x
d
x
e
i
n
w
x
d
w
f(x)=frac{1}{2pi}int^infty_{-infty}int^infty_{-infty}f(x)e^{-inwx}dxe^{inwx}dw
f(x)=2π1∫−∞∞∫−∞∞f(x)e−inwxdxeinwxdw
这个公式是个“套娃”,其中
∫
−
∞
∞
f
(
x
)
e
−
i
n
w
x
d
x
int^infty_{-infty}f(x)e^{-inwx}dx
∫−∞∞f(x)e−inwxdx是一个关于
w
w
w的函数(x被积分了),于是有
F
(
w
)
=
∫
−
∞
∞
f
(
x
)
e
−
i
w
x
d
x
F(w)=int^infty_{-infty}f(x)e^{-iwx}dx
F(w)=∫−∞∞f(x)e−iwxdx,这是一个对于
f
(
x
)
f(x)
f(x)的变换,最后得到的是一个关于频率相关的
w
w
w的函数
(
w
=
n
w
)
(w=nw)
(w=nw),也就是由时域向频域的变换。(变换)
带入
F
(
w
)
F(w)
F(w)之后,原式为
f
(
x
)
=
1
2
π
∫
−
∞
∞
F
(
w
)
e
i
w
x
d
w
f(x)=frac{1}{2pi}int^infty_{-infty}F(w)e^{iwx}dw
f(x)=2π1∫−∞∞F(w)eiwxdw是一个关于x的函数(
w
w
w被积分了),并且是一个由频域向时域的变换,也是之前变换的逆。(逆变换)
这样从傅里叶级数要求的周期性函数,变成了一般的函数,但是其函数仍需要满足傅里叶级数中提到的狄里赫莱条件才能进行运用。