递归的实现原理

需要用到递归的3种情况：

（1）定义是递归的

例如计算阶乘的递归函数

longFactorial(longn){
    if(n==0) return1;
    elsereturnn*Factorial(n-1);
}

(2)数据结构是递归的

例如搜索单链表最后一个结点的算法

LinkNode *FindRear(LinkNode *f){
    if(f==NULL) returnNULL;
    elseif(f->link==NULL) returnf;
    elsereturnFindRear(f->link);
}

在单链表中搜索值等于x的结点

voidSearch(LinkNode *f,T& x){
    if(f==NULL) return;
    elseif(f->data==x) returnf;
    elsereturnSearch(f->link,x); 
}

（3）问题的解法是递归的

例如如汉诺塔问题：先将n-1个盘子移动到b柱子，再把最下面的盘子移动到c柱，再把n-1个盘子移动到c柱。T(n)=2T(n-1)+1=2ⁿ-1。

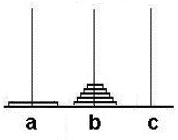
又例如辗转求余法求724和344的最大公约数：

int GCD(int m , int n){
    if(m<0) m=-m;
    if(n<0) n=-n;
    if(n==0) return m;
    return GCD(n , m%n);
}

GCD(724 , 344)=GCD(344 , 36)=GCD(36 , 20)=GCD(20 , 16)=GCD(16 ,4)=GCD(4 , 0)=4

可以这么递归的原因：

假设a=qb+r，r=a%b

若a和b有公因子d（d|a且d|b），则d也是a-qb=r的因子，故d是b和r的公因子（d|b且d|r）

若b和r有公因子d（d|b且d|r），则d也是r+qb=a的因子，故d是a和b的公因子（d|a且d|b）

因此a和b的公因子集合、b和r的公因子集合是相同的

递归工作栈

IA-32使用栈来支持过程的嵌套调用。每个过程都有自己的栈区，称为栈帧（stack frame）。因此，一个栈由若干栈帧组成，每个栈帧用专门的帧指针寄存器EBP指定起始位置，当前栈帧的范围在其和栈指针寄存器ESP指向区域之间。

IA-32规定，寄存器EAX、ECX和EDX是调用者保存寄存器。当过程P调用过程Q时，Q 可以直接使用这三个寄存器，不用将它们的值保存到栈中，这也意味着，如果P在从Q返回后还要用这三个寄存器的话，P应在转到Q之前先保存它们的值，并在从Q返回后先恢复它们的值再使用。寄存器EBX、ESl、EDI是被调用者保存寄存器，Q必须先将它们的值保存到栈中再使用它们，并在返回P之前先恢复它们的值。

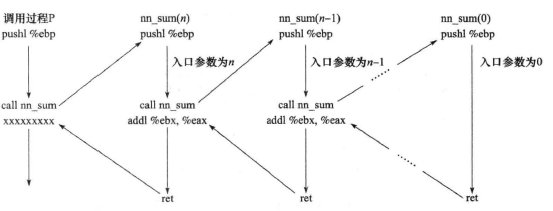
（1）每次递归调用前，先将参数n~参数1按序复制到调用过程栈帧中

（2）执行call指令：首先将返回地址（call指令要执行时EIP的值，即call指令下一条指令的地址）压入栈顶，然后将程序跳转到当前调用的方法的起始地址，相当于执行了push和jump指令。

递归调用时，每一层调用过程栈帧中存放的返回地址都是相同的。

（3）每次递归，必定要先push %ebp（把原帧指针保存在栈顶）和mov %esp,%ebp（把存放原帧指针的栈顶，设置为新栈底）

被调用者定义的非静态局部变量仅存放于当前栈帧，调用结束后就被释放了。

最后往往通过EAX寄存器将结果返回给调用者。

（4）执行leave指令：将栈指针指向帧指针，然后pop备份栈顶存放的原帧指针到EBP。

（5）最后执行ret指令：将栈顶的返回地址弹出到EIP，然后按照EIP此时指示的指令继续执行程序。

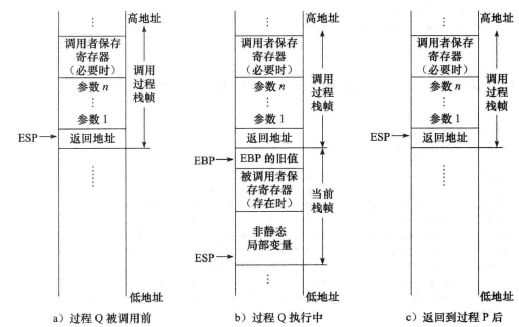
如图所示，Q的过程体执行时，入口参数1的地址总是R[ebp]+8，入口参数2的地址总是R[ebp]+12……（在栈中传递的参数若是基本类型，则都被分配4个字节）

与IA-32不同，x86-64最多可有6个整型或指针型参数通过寄存器传递，超过6个入口参数时，后面的通过栈来传递。在栈中传递的参数若是基本类型，则都被分配8个字节。栈中的地址也变为了8个字节。

RAX、R10和R11为调用者保存寄存器。RBX、RBP、R12、R13、R14和R15为被调用者保存寄存器，需要将它们先保存在栈中再使用，最后返回前再恢复其值。

过程调用中使用的栈机制和寄存器使用约定，使得可以进行过程的嵌套调用和递归调用。

理解了递归的实现原理后，对于递归过程，就可以用栈将它改为非递归过程，如用栈帮助求解斐波那契函数的非递归算法

struct Node{   //栈结点的类定义
    longn;    //记忆走过的n
    inttag;   //区分左右递归的标志
}
longFibnacci(longn){
    Stack<Node> S ;
    Node *w;
    longsum=0;
    do{
        while(n>1){
            w->n=n;
            w->tag=1;
            S.push(w);
            n--;
        }
        sum=sum+n;
        while(!S.IsEmpty()）{
            S.Pop(w);
            if(w->tag==1){    //tag==1表示向左递归
                w->tag=2;     //tag==2表示向右递归
                S.push(w);
                n=w->n-2;
                break;
            }
        }
    }while(!S.IsEmpty())；
}

直接用递归法、或是借助栈求解斐波那契函数的时间复杂度是O(2ⁿ)，因此可改用迭代法

longFibIter(longn){
    if(n<=1) returnn;
    longtwoback=0,oneback=1,Current;
    for(i=2;i<=n;i++){
        Current=twoback+oneback;  //计算Fib(i-2)+Fib(i-1)的值
        twoback=oneback;     //把Fib(i-1)的值保存作为下一次的Fib(i-2)
        oneback=Current;     //把Fib(i)的值保存作为下一次的Fib(i-1)
    }
    returnCurrent;
}

如果觉得斐波那契函数的非递归算法不好理解，可以举一个更简单的例子：

逆向打印数组A[]中数值的递归算法

voidrecfunc(intA[],intn){
    if(n>=0){
        cout<<A[n]<<",";
        n--;
        recfunc(A,n);
    }
}

改用迭代算法

voiditerfunc(intA[],intn){
    while(n>=0){
        count<<A[n]<<",";
        n--;
    }
}