1. 偏导数
偏导数 $ eq$ 偏导函数。偏导数是偏导函数在某点的函数值
在点 $(x_{0},y_{0})$ 处对 $x$ 和 $y$ 的偏导数分别为
$$f_{x}^{'}(x_{0},y_{0}) = lim_{Delta x ightarrow 0}frac{f(x_{0} + Delta x, y_{0}) - f(x_{0}, y_{0})}{Delta x} = frac{d}{dx}f(x,y_{0})|_{x=x_{0}}$$
$$f_{y}^{'}(x_{0},y_{0}) = lim_{Delta y ightarrow 0}frac{f(x_{0}, y_{0}+ Delta y) - f(x_{0}, y_{0})}{Delta y} = frac{d}{dy}f(x_{0},y)|_{y=y_{0}}$$
将 $x_{0},y_{0}$ 泛化,可得偏导函数:
$$f_{x}^{'}(x, y) = lim_{Delta x ightarrow 0}frac{f(x + Delta x, y) - f(x, y)}{Delta x} = frac{partial f(x,y)}{partial x}$$
$$f_{y}^{'}(x, y) = lim_{Delta y ightarrow 0}frac{f(x, y + Delta y) - f(x, y)}{Delta y} = frac{partial f(x,y)}{partial y}$$
偏导函数是二元函数,在求的过程中,将另一维的变量当作常量,然后根据一元函数导函数求法来求偏导函数。比如二元函数固定 $y$,只让 $x$ 单
独变化,从而看成是关于 $x$ 的一元函数的变化来研究。
虽然求偏导函数的时候将另一维变量当成常量,但其本身也是一个变量,所以将 $d$ 变成 $partial$,表示多元函数求偏导。不同于一元,$partial$ 没有微分的含义,
只是一个记号,$partial$ 或 $d$ 和其后面跟的变量是可分离的。
注意:$f_{x}^{'}$ 并不是代表对 $x$ 求偏导,而是相当于 $f_{1}^{'}$,由于不是复合函数,所以间接认为是对变量 $x$ 求偏导。
求某点偏导数的方法:
1)将该点代入偏导函数,可直接计算得到函数值
2)既然另一维变量在求偏导的过程中是看作常量的,则可将另一维变量值直接代入原函数,然后根据一元函数导数求法来求。
偏导数的几何意义是曲线在某点的切线斜率,这个曲线是二元函数图形张成的曲面与平面 $x = x_{0}$ 或 平面 $y = y_{0}$ 的交线。
偏导函数就是所有这样的曲线的导函数所组成的曲面。可以想象:每条曲线位于每个不同的平面内,互不干扰,它们的导函数自然也位于自己所在
的平面内,互不干扰,然后每个平面上的导函数曲线的组合就会构成偏导函数的曲面。
但是由于曲面上一点的切线有无数条(实际上是个切面),每一个切线都代表一个变化的方向,每个切线的斜率都代表一个方向的变化率。
但是如果我们想求任意一条曲线切线斜率怎么办呢?这时候就引入了方向导数。
理解一下这个方向的含义:对 $x$ 或 $y$ 的偏导数其实是对 $x$ 轴方向或 $y$ 轴方向的偏导数,所以这个方向并不是切线方向,而是切线方向
在 $xoy$ 平面上投影后形成的射线方向,平面上射线方向和空间切线方向一一对应。
方向导数定义:设函数 $f(x,y)$ 在平面上任意一点 $P(x,y)$ 的邻域内有定义,自 $P$ 点引出一条射线 $l$,这个射线是空间中对应的切线方向
在 $xoy$ 平面上的投影,在 $l$ 上取一点 $(x + Delta x, y + Delta y)$,设该点到 $P$ 的距离为 $ ho$,则 $ ho = sqrt{(Delta x)^{2} + (Delta y)^{2}}$,若极限
$$lim_{ ho ightarrow 0}frac{f(x + Delta x, y + Delta y) - f(x, y)}{ ho }$$
存在,则称此极限值为 $f(x,y)$ 在点 $P$ 沿方向 $l$ 的方向导数,记为 $frac{partial f}{partial l} $。
设 $l$ 与 $x$ 轴的夹角为 $alpha$,则方向导数也可以写成
$$frac{partial f}{partial l} = lim_{ ho ightarrow 0}frac{f(x + ho cdot cosalpha ,; y + ho cdot sinalpha) - f(x, y)}{ ho } $$
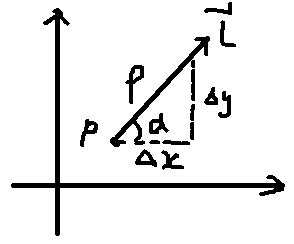
由图像可知
$$cos alpha = frac{Delta x}{ ho}= frac{Delta x}{sqrt{(Delta x)^{2} + (Delta y)^{2}}}$$
$$sin alpha = frac{Delta y}{ ho}= frac{Delta y}{sqrt{(Delta x)^{2} + (Delta y)^{2}}}$$
要使任意方向的导数都存在,则函数在该点必须可微,根据增量表达式
$$f(x+Delta x,y+Delta y) - f(x,y) = Acdot Delta x + Bcdot Delta y + o( ho )$$
两边同时除以 $ ho$,并取极限,可得
$$frac{partial f}{partial l} = frac{partial f}{partial x}cos alpha + frac{partial f}{partial y}sin alpha = (frac{partial f}{partial x}, frac{partial f}{partial y}) cdot (cos alpha,sin alpha)$$
梯度:它是一个方向向量,是函数在某点无数个变化方向中变化最快的那个方向,也是方向导数最大的方向。通过上式可以发现,只要每一个
变量都沿着关于这个变量的偏导所指定的方向来变化,函数的整体变化就能达到最快(变化的绝对值最大),梯度记为
$$gradz = (frac{partial f}{partial x},frac{partial f}{partial y})$$
2. 全微分
先来看看一元微分给了我们什么启示:
1)微分得是“直”的(这样才能“代曲”),一元是直线,二元只能是平面。
2)微分和切线有关,一元微分就是切线,二元微分是由无数条切线张成的切平面。
所以要使二元的函数能够微分,则每个点所有方向的切线必须都存在,并且都在一个平面,也叫切平面,这个微分可以提供对曲面很好的“线性近似”。
“线性逼近,以直代曲”是微积分的精髓所在。下面我们来看下全微分的定义。
函数 $z=f(x, y)$ 在点 $(x, y)$ 处的全增量为
$$Delta z = f(x+Delta x,y+Delta y) - f(x,y)$$
如果全增量可以表示为
$$Delta z = f(x+Delta x,y+Delta y) - f(x,y) = Acdot Delta x + Bcdot Delta y + o( ho ),; ho = sqrt{(Delta x)^{2} + (Delta y)^{2}} ; and ; ho ightarrow 0$$
其中 $A,B$ 不依赖于 $Delta x,Delta y$,只与 $x,y$ 有关,则称函数 $z=f(x, y)$ 在点 $(x, y)$ 处可微,全微分记为
$$dz = Acdot Delta x + Bcdot Delta y$$
那这个 $A$ 和 $B$ 如何计算呢?
$$f(x+Delta x,y+Delta y) - f(x,y) = Acdot Delta x + Bcdot Delta y + o(
ho ) \
let ; Delta y = 0 \
f(x+Delta x,y) - f(x,y) = Acdot Delta x + o(|Delta x|) \
both ; sizes ; divedes ; Delta x \
A = frac{partial f}{partial x}$$
同理: $B = frac{partial f}{partial y}$,又无穷小时 $Delta x = dx,; Delta y = dy$,所以全微分为
$$dz = frac{partial f}{partial x}dx + frac{partial f}{partial y}dy$$