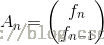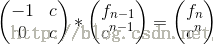矩阵快速幂

一、前期铺垫

　在讲矩阵快速幂之前，我们先来看一下整数快速幂。求 X 的 N 次方。

　举个例子，在求 x^19时，我们可以拆分成 x^16、x^2 和 x的乘积。我们观察19的二进制数（10011），发现二进制第 i 位上的值为 1 ，在乘积中就要有 x 的 2^i 的一项。据此我们可以利用遍历二进制数的每一位快速求出 X^N。

　代码如下：

 1 ll QuickPow(ll x,ll n)
 2 {
 3     ll tmp = (ll)x;
 4     ll res = 1;
 5     for(ll i=0;(1<<i)<=n;i++)
 6     {
 7         if(n&(1<<i))
 8         {
 9             res=(res*tmp)%mod;
10         }
11         tmp=(tmp*tmp)%mod;
12     }
13     return res;
14 }

也可以写成下面这样：

 1 ll QuickPow(ll x,ll n)
 2 {
 3     ll tmp = x;
 4     ll res=1;
 5     while(n)
 6     {
 7         if(n&1)
 8             res=(res*tmp)%mod;
 9         tmp = (tmp*tmp)%mod;
10         n>>=1;
11     }
12     return res;
13 }

二、矩阵快速幂的实现过程

　　现在问题变成求解矩阵 A 的 N 次方，我们可以类比整数快速幂，写一个矩阵的结构体，用一个matmul函数来定义矩阵的乘法，具体实现过程与整数快速幂类似。

struct mat
{
    ll m[maxn][maxn];
}unit;
void init()
{
    for(int i=1;i<maxn;i++)
        unit.m[i][i]=1;
}
mat matmul(mat a,mat b)
{
    mat ans;
    ll tmp =0;
    for(int i=1;i<maxn;i++)
    {
        for(int j=1;j<maxn;j++)
        {
            tmp=0;
            for(int k=1;k<maxn;k++)
            {
                tmp=(tmp+a.m[i][k]*b.m[k][j])%mod;
            }
            ans.m[i][j]=tmp;
        }
    }
    return ans;
}
mat QuickPow(mat a,ll n)
{
    mat tmp = a;
    mat res=unit;
    while(n)
    {
        if(n&1)
            res=matmul(res,tmp);
        tmp = matmul(tmp,tmp);
        n>>=1;
    }
    return res;
}

三、应用

第一步先要列出递推式:

例如 f(n) = f(n-1) + f(n-2)

第二步是建立矩阵递推式，找到转移矩阵:

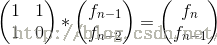
简写成T * A(n-1)=A(n)，T矩阵就是转移矩阵，而且一定是一个常数矩阵，

由此得到A(n)= A(1) * T^(n-1)

T^(n-1)可以利用矩阵快速幂计算出来，而A(1)可以手动计算，就可以得到A(n)

给一些简单的递推式
1.f(n)=a*f(n-1)+b*f(n-2)+c；（a,b,c是常数）

2.f(n)=c^n-f(n-1) ；（c是常数）

参考博客：https://blog.csdn.net/wust_zzwh/article/details/52058209