题意:
简略题意: 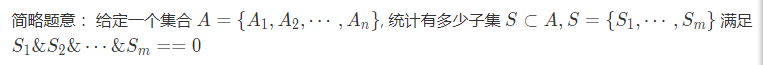
n <= 1e6,0 <= A[i] <= 1e6
首先有一个很显然的n * A[i]的子集DP,这里就不再赘述
这题的难点在于把数字看成集合,然后求若干个集合并起来为空的方案数,并起来为空很不想,我们可以考虑并起来恰好有0个元素,"恰好"是不是有二次项反演那感觉了?可惜这题限制条件太多,不好反演或者反演不了
但这给我们启发,毕竟一切二次项反演题基本都可以用容斥来做,我们可以考虑用容斥来做,加上并起来恰好为0个元素的,减去恰好为1个元素的......所以我们现在要求有多少个集合并起来至少有i个元素,转化为数字即(bit(x) == i)
(bit[x]即x的二进制下有几个一),我们可以先钦定有x个元素,即枚举x的超集,设为dp[x],从数字上也可以理解为(满足A[i] & x == A[i])的i有多少个,这个显然可以枚举子集暴力DP,然后每个x的超集可以可选可不选,但不能全不选(全不选并完就变成了空集)
所以对于单个数x贡献是2^dp[x] - 1;然后容斥一下即可(注意在集合和数字间转化,个人觉得是本题最大难点)
代码如下:
/*阴影之内*/
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
#define ll long long
int read(){
char c = getchar();
int x = 0;
while(c < '0' || c > '9') c = getchar() ;
while(c >= '0' && c <= '9') x = x * 10 + c - 48,c = getchar() ;
return x;
}
const int maxn = 1e6 + 10;
const int mod = 1e9 + 7;
int dp[maxn];
int mi[maxn];
void init(){
mi[0] = 1;
for(int i = 1; i <= maxn - 10; ++i) mi[i] = 2ll * mi[i-1] % mod;
}
int main(){
int n = read();
init();
for(int i = 1; i <= n; ++i){
int x = read();dp[x]++;
}
for(int i = 0; i <= 20; ++i)
for(int j = 0; j <= maxn - 10; ++j)
if(j & (1 << i))
dp[j^(1<<i)] += dp[j];
ll Ans = 0;
for(int i = 0; i <= maxn - 10; ++i){
int num = 0;
for(int j = 0; j <= 20; ++j)
if(i & (1 << j)) num++;
if(num & 1) Ans = (Ans - (mi[dp[i]] - 1) + mod) % mod;
else Ans = (Ans + (mi[dp[i]] - 1)) % mod;
}
cout<<Ans<<endl;
return 0;
}