一、相关定义
最短路径:从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径。
地位:Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构、图论、运筹学等等。
缺陷:若有一个带负权回路的图(即一个不存在最短路径的图),Dijkstra算法无法检测出这个问题。
时间复杂度:O(n2),若进行堆优化,可降为O(n*logn)。
二、算法描述
主要变量如下:
int n 表示有n个点,从1~n标号
int s,t s为源点,t为终点
int dis[N] 记录每一个点到源点的估计距离
int pre[N] 记录路径,pre[i]表示i的前驱结点
bool vis[N] vis[i]=true表示点i被标记
【初始化】
将图的顶点分成两个集合S、U。初始时S中只有源点,而U中是其余的点(即V-S)。
有一个dis[n](n为图的节点数)的数组来记录每一个点到源点的路径长度。
【基本思想】
设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
【过程分析】
初始时,S中仅含有源。设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dis记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从U中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dis作必要的修改。一旦S包含了所有V中顶点(即S=V),dis就记录了从源到所有其它顶点之间的最短路径长度。
例如,对下图中的有向图,应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。

Dijkstra算法的迭代过程:
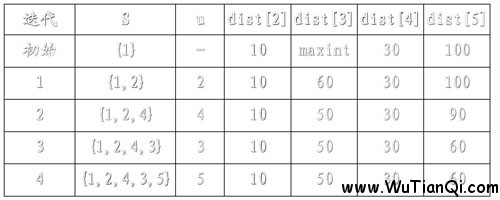
【复杂度】
Dijkstra 每次循环都可以确定一个顶点的最短路径,故程序需要循环 n-1 次。
【举例分析】
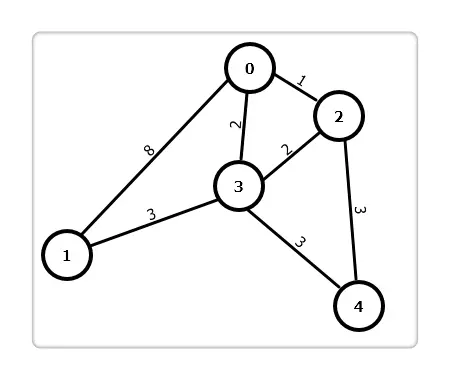
定义源点为 0,dis[i]为源点 0 到顶点 i 的最短路径。其过程描述如下:
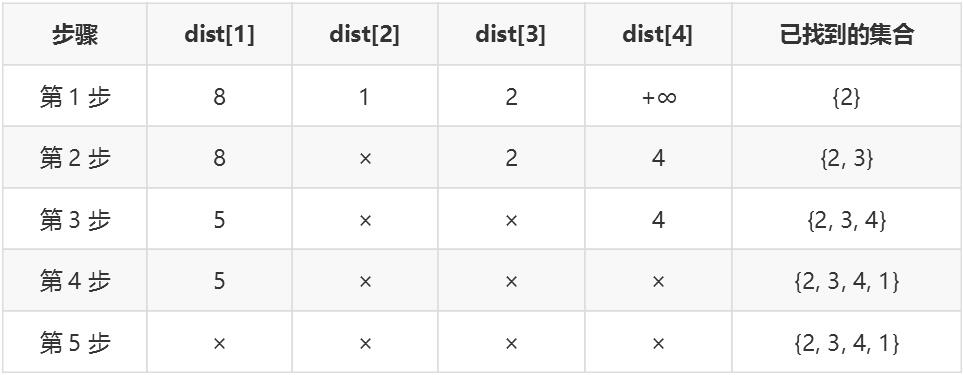
第 1 步:从源点 0 开始,找到与其邻接的点:1,2,3,更新dis[]数组,因 0 不与 4 邻接,故dis[4]为正无穷。在dis[]中找到最小值,其顶点为 2,即此时已找到 0 到 2 的最短路。
第 2 步:从 2 开始,继续更新dis[]数组:2 与 1 不邻接,不更新;2 与 3 邻接,因0→2→3比dis[3]大,故不更新dis[3] ;2 与 4 邻接,因0→2→4比dis[4]小,故更新dis[4]为 4。在dis[]中找到最小值,其顶点为 3,即此时又找到 0 到 3 的最短路。
第 3 步:从 3 开始,继续更新dis[]数组:3 与 1 邻接,因0→3→1比dis[1]小,更新dis[1]为 5;3 与 4 邻接,因0→3→4比dis[4]大,故不更新。在dis[]中找到最小值,其顶点为 4,即此时又找到 0 到 4 的最短路。
第 4 步:从 4 开始,继续更新dis[]数组:4 与 1 不邻接,不更新。在dis[]中找到最小值,其顶点为 1,即此时又找到 0 到 1 的最短路。
第 5 步:所有点都已找到,停止。
对于上述步骤,你可能存在以下的疑问:

若 A 作为源点,与其邻接的只有 B,C,D 三点,其dist[]最小时顶点为 C,即就可以确定A→C为 A 到 C 的最短路。但是我们存在疑问的是:是否还存在另一条路径使 A 到 C 的距离更小? 用反证法证明。
假设存在如上图的红色虚线路径,使A→D→C的距离更小,那么A→D作为A→D→C的子路径,其距离也比A→C小,这与前面所述 “dist[]最小时顶点为 C” 矛盾,故假设不成立。因此这个疑问不存在。
根据上面的证明,我们可以推断出,Dijkstra 每次循环都可以确定一个顶点的最短路径,故程序需要循环 n-1 次。
三、代码实现
#include<iostream>
using namespace std;
int matrix[100][100]; //邻接矩阵
bool visited[100]; //标记数组
int dist[100]; //源点到顶点i的最短距离
int path[100]; //记录最短路的路径
int source; //源点
int vertex_num; //顶点数
int arc_num; //弧数
void Dijkstra(int source)
{
memset(visited, 0, sizeof(visited)); //初始化标记数组
visited[source] = true;
for (int i = 0; i < vertex_num; i++)
{
dist[i] = matrix[source][i];
path[i] = source;
}
int min_cost; //权值最小
int min_cost_index; //权值最小的下标
for (int i = 1; i < vertex_num; i++) //找到源点到另外vertex_num-1个点的最短路径
{
min_cost = INT_MAX;
for (int j = 0; j < vertex_num; j++)
{
if (visited[j] == false && dist[j] < min_cost) //找到权值最小
{
min_cost = dist[j];
min_cost_index = j;
}
}
visited[min_cost_index] = true; //该点已找到,进行标记
for (int j = 0; j < vertex_num; j++) //更新dist数组
{
if (visited[j] == false &&
matrix[min_cost_index][j] != INT_MAX && //确保两点之间有弧
matrix[min_cost_index][j] + min_cost < dist[j])
{
dist[j] = matrix[min_cost_index][j] + min_cost;
path[j] = min_cost_index;
}
}
}
}
int main()
{
cout << "请输入图的顶点数(<100):";
cin >> vertex_num;
cout << "请输入图的弧数:";
cin >> arc_num;
for (int i = 0; i < vertex_num; i++)
for (int j = 0; j < vertex_num; j++)
matrix[i][j] = INT_MAX; //初始化matrix数组
cout << "请输入弧的信息:
";
int u, v, w;
for (int i = 0; i < arc_num; i++)
{
cin >> u >> v >> w;
matrix[u][v] = matrix[v][u] = w;
}
cout << "请输入源点(<" << vertex_num << "):";
cin >> source;
Dijkstra(source);
for (int i = 0; i < vertex_num; i++)
{
if (i != source)
{
cout << source << "到" << i << "最短距离是:" << dist[i] << ",路径是:" << i;
int t = path[i];
while (t != source)
{
cout << "--" << t;
t = path[t];
}
cout << "--" << source << endl;
}
}
return 0;
}
输入数据,结果为:

代码2:
#include <iostream>
using namespace std;
const int maxnum = 100;
const int maxint = 999999;
// 各数组都从下标1开始
int dist[maxnum]; // 表示当前点到源点的最短路径长度
int prev[maxnum]; // 记录当前点的前一个结点
int c[maxnum][maxnum]; // 记录图的两点间路径长度
int n, line; // 图的结点数和路径数
// n -- n nodes
// v -- the source node
// dist[] -- the distance from the ith node to the source node
// prev[] -- the previous node of the ith node
// c[][] -- every two nodes' distance
void Dijkstra(int n, int v, int *dist, int *prev, int c[maxnum][maxnum])
{
bool s[maxnum]; // 判断是否已存入该点到S集合中
for(int i=1; i<=n; ++i)
{
dist[i] = c[v][i];
s[i] = 0; // 初始都未用过该点
if(dist[i] == maxint)
prev[i] = 0;
else
prev[i] = v;
}
dist[v] = 0;
s[v] = 1;
// 依次将未放入S集合的结点中,取dist[]最小值的结点,放入结合S中
// 一旦S包含了所有V中顶点,dist就记录了从源点到所有其他顶点之间的最短路径长度
// 注意是从第二个节点开始,第一个为源点
for(int i=2; i<=n; ++i)
{
int tmp = maxint;
int u = v;
// 找出当前未使用的点j的dist[j]最小值
for(int j=1; j<=n; ++j)
if((!s[j]) && dist[j]<tmp)
{
u = j; // u保存当前邻接点中距离最小的点的号码
tmp = dist[j];
}
s[u] = 1; // 表示u点已存入S集合中
// 更新dist
for(int j=1; j<=n; ++j)
if((!s[j]) && c[u][j]<maxint)
{
int newdist = dist[u] + c[u][j];
if(newdist < dist[j])
{
dist[j] = newdist;
prev[j] = u;
}
}
}
}
// 查找从源点v到终点u的路径,并输出
void searchPath(int *prev,int v, int u)
{
int que[maxnum];
int tot = 1;
que[tot] = u;
tot++;
int tmp = prev[u];
while(tmp != v)
{
que[tot] = tmp;
tot++;
tmp = prev[tmp];
}
que[tot] = v;
for(int i=tot; i>=1; --i)
if(i != 1)
cout << que[i] << " -> ";
else
cout << que[i] << endl;
}
int main()
{
freopen("input.txt", "r", stdin);
// 各数组都从下标1开始
// 输入结点数
cin >> n;
// 输入路径数
cin >> line;
int p, q, len; // 输入p, q两点及其路径长度
// 初始化c[][]为maxint
for(int i=1; i<=n; ++i)
for(int j=1; j<=n; ++j)
c[i][j] = maxint;
for(int i=1; i<=line; ++i)
{
cin >> p >> q >> len;
if(len < c[p][q]) // 有重边
{
c[p][q] = len; // p指向q
c[q][p] = len; // q指向p,这样表示无向图
}
}
for(int i=1; i<=n; ++i)
dist[i] = maxint;
for(int i=1; i<=n; ++i)
{
for(int j=1; j<=n; ++j)
printf("%8d", c[i][j]);
printf("
");
}
Dijkstra(n, 1, dist, prev, c);
// 最短路径长度
cout << "源点到最后一个顶点的最短路径长度: " << dist[n] << endl;
// 路径
cout << "源点到最后一个顶点的路径为: ";
searchPath(prev, 1, n);
}
测试数据:点击
Dijkstar 算法+堆优化
//使用优先队列优化,复杂度 O (E log E)
/*
* 使用优先队列优化Dijkstra算法
* 复杂度O(ElogE)
* 注意对vector<Edge>E[MAXN]进行初始化后加边
*/
const int INF=0x3f3f3f3f; //防止后面溢出,这个不能太大
const int MAXN=1000010;
struct qnode
{
int v;
int c;
qnode(int _v=0,int _c=0):v(_v),c(_c){}
bool operator <(const qnode &r)const
{
return c>r.c;
}
};
struct Edge
{
int v,cost;
Edge(int _v=0,int _cost=0):v(_v),cost(_cost){}
};
vector<Edge>E[MAXN];
bool vis[MAXN];
int dist[MAXN];
void Dijkstra(int n,int start)//点的编号从1开始
{
memset(vis,false,sizeof(vis));
for(int i=1;i<=n;i++)dist[i]=INF;
priority_queue<qnode>que;
while(!que.empty())que.pop();
dist[start]=0;
que.push(qnode(start,0));
qnode tmp;
while(!que.empty())
{
tmp=que.top();
que.pop();
int u=tmp.v;
if(vis[u])continue;
vis[u]=true;
for(int i=0;i<E[u].size();i++)
{
int v=E[tmp.v][i].v;
int cost=E[u][i].cost;
if(!vis[v]&&dist[v]>dist[u]+cost)
{
dist[v]=dist[u]+cost;
que.push(qnode(v,dist[v]));
}
}
}
}
void addedge(int u,int v,int w)
{
E[u].push_back(Edge(v,w));
}