说在前面
微积分由于刚刚学习,所以趁着有印象赶快整理下来
本文章适合入门,其实文章里面大部分都是有关于导数的内容,积分内容只有两个
平均变化率
概念:一般的,已知函数y=f(x),x0,x1是其定义域不同的两点,记作: (Delta) x=x1-x0
(Delta)y=y1-y0=f(x1)-f(x0)=f(x0+(Delta)x)-f(x1)
则当(Delta)x!=0时,商(dfrac {Delta y}{Delta x})=(dfrac {fleft( x_{0}+Delta x
ight) -fleft( x_{0}
ight) }{Delta x})
称函数y=f(x)在区间[x0,x0+(Delta)x](或[x0+(Delta)x,x0])的平均变化率
例题:1.求函数y=x^2在区间[x0,x0+(Delta)x]的平均变化率
2.求函数y=(dfrac {1}{x})在区间[x0,x0+(Delta)x]的平均变化率
瞬时变化率
概念:当(Delta)x趋近于0时,平均变化率(dfrac {Delta y}{Delta x})=(dfrac {fleft( x_{0}+Delta x
ight) -fleft( x_{0}
ight) }{Delta x})趋近于一个常数l
那么称函数l为函数y=f(x)在点x0的瞬时变化率
记作:当(Delta)x ——> 0时,(dfrac {fleft( x_{0}+Delta x
ight) -fleft( x_{0}
ight) }{Delta x}) ——> l
即(lim _{Delta x ightarrow 0}dfrac {f_{c}left( x_{0}+Delta x ight) -fleft( x_{0} ight) }{Delta x}=l)
f(x)在点x0处的导数
概念:函数y=f(x)在点x0的瞬时变化率
通常称为f(x)在点x0处的导数,并记作(f'left( x_{0}
ight))
(lim _{Delta x
ightarrow 0}dfrac {f_{c}left( x_{0}+Delta x
ight) -fleft( x_{0}
ight) }{Delta x}=f'left( x_{0}
ight))
导数定义
概念:如果f(x)在开区间(a,b)内每一点x都是可导的,称f(x)在区间(a,b)可导
区间(a,b)的每个值都对应一个确定的导数(f'left( x
ight))
于是在区间(a,b)内,(f'left( x
ight))可构成一个新函数
称为y=f(x)的导函数,记作(f'left( x
ight))通称导数
例题:1.火箭竖直向上发射,熄火时向上速度达到100m/s
试问熄火多长时间火箭上上速度为(0)
2.圆S=π r^2,周长l=2πr求之间的关系
导数的几何意义
概念:通过直线和曲线图像我们可以得知两线有割线也有切线
显然,我们可以知道割线的斜率就是平均变化率
当割线成为切线的时候(Delta)x ——>(0),割线斜率趋近于切线斜率
即(lim _{Delta x
ightarrow 0}dfrac {f_{c}left( x_{0}+Delta x
ight) -fleft( x_{0}
ight) }{Delta x}=f'left( x_{0}
ight))
例题:1.求抛物线(y=x^{2})在点(x0,f(x0))的导数的切线的斜率等于(f'left( x_{0}
ight))
2.求双曲线(y=dfrac {1}{x})在点(2,1/2)的切线方程
导数的运算
常值函数的导数:
(y=fleft( x
ight) equiv c)(c为常数)
(y'=f'left( x
ight) =C'=lim _{Delta x
ightharpoonup 0}dfrac {c-c}{Delta x}=0)
根据以上的方法我们可以得到几个式子
y=x y'=x'=1
(y=x^{2}) (y=left(x^{2}
ight)'=2x)
(y=dfrac {1}{x}) (y'=-dfrac {1}{x^{2}})
(y=x^{3}) (y'=3x^{2})
(y=sqrt {x}) (y'=lim _{Delta x
ightarrow 0}dfrac {sqrt {x_{0}+Delta }x-sqrt {x_{0}}}{Delta x})
基本初等函数的公示表

导数的四则运算
1.函数和或差的求法
(left[ fleft( x ight) pm gleft( x ight) ight] '=f'left( x ight) pm g'left( x ight))
2.函数积的求法
(left[ tleft( x ight) cdot gleft( x ight) ight] '=f'left( x ight) cdot gleft( x ight) +g'left( x ight) cdot fleft( x ight))
3.函数商的求法
(left[ dfrac {fleft( x ight) }{gleft( x ight) } ight]' =dfrac {f'left( x ight) gleft( x ight) -fleft( x ight) g'left( x ight) }{g^{2}left( x ight) })
利用导数判断函数的单调性
1.在区间(a,b)为$f'left( x ight) $>0则f(x)在此区间为增函数,此区间为此函数的增区间
2.在区间(a,b)为$f'left( x ight) $<0则f(x)在此区间为减函数,此区间为此函数的减区间
利用导数研究函数的极值

曲边梯形与定积分
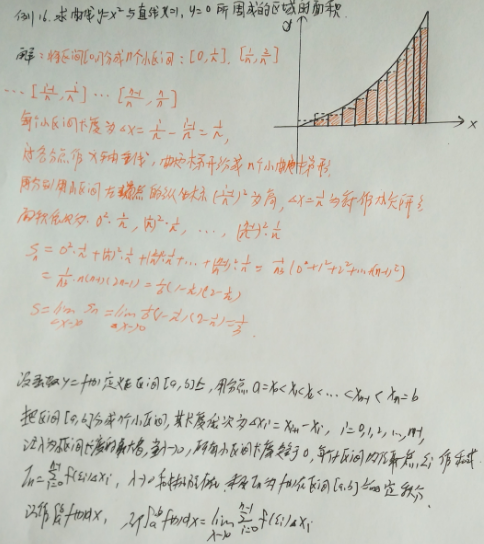
微积分基本定理

补充:定积分


