损失函数
我们在进行机器学习任务时,使用的每一个算法都有一个目标函数,算法便是对这个目标函数进行优化,特别是在分类或者回归任务中,便是使用损失函数(Loss Function)作为其目标函数,又称为代价函数(Cost Function)。损失函数是用来估量模型的预测值f(x)与真实值Y的不一致程度,它是一个非负实值函数,通常使用L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好。损失函数是经验风险函数的核心部分,也是结构风险函数重要组成部分。模型的结构风险函数包括了经验风险项和正则项,通常可以表示成如下式子:
$Jleft ( mathbf{w} ight )=sum_{i}Lleft ( m_ileft (mathbf{ w} ight ) ight )+lambda Rleft ( mathbf{w} ight )$
其中,$Lleft ( m_ileft (mathbf{ w} ight ) ight )$为损失项,$Rleft ( mathbf{w} ight )$.$m_i$的具体形式如下:
$m_i=y^{left ( i ight )}f_mathbf{w}left ( mathbf{x}^{left ( i ight )} ight )$
$y^{left ( i ight )}in left { -1,;1 ight }$
$f_mathbf{w}left ( mathbf{x}^{left ( i ight )} ight )=mathbf{w}^Tmathbf{x}^{(i)}$
常见的损失函数:
1.log对数损失函数(逻辑回归)
$L(Y,P(Y|X)) = -log P(Y|X)$
损失函数L(Y, P(Y|X))表达的是样本X在分类Y的情况下,使概率P(Y|X)达到最大值(换言之,就是利用已知的样本分布,找到最有可能(即最大概率)导致这种分布的参数值;或者说什么样的参数才能使我们观测到目前这组数据的概率最大)。这种损失函数的目的是最大化预测值为真实值的概率。
逻辑回归的P(Y=y|x)表达式如下:
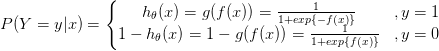
分类器可以表示为:
$pleft ( ymid mathbf{x}; mathbf{w} ight )=sigma left ( mathbf{w}^Tmathbf{x} ight )^yleft ( 1-sigma left ( mathbf{w}^Tmathbf{x} ight ) ight )^{left ( 1-y ight )}$
为了求解其中的参数w,通常使用极大似然估计的方法,具体的过程如下:
1.似然函数
$Lleft ( mathbf{w} ight )=prod_{i=1}^{n}sigma left ( mathbf{w}^Tmathbf{x}^{left ( i ight )} ight )^{y^{left ( i ight )}}left ( 1-sigma left ( mathbf{w}^Tmathbf{x}^{left ( i ight )} ight ) ight )^{left ( 1-y^{left ( i ight )} ight )}$
$sigma left ( x ight )=frac{1}{1+expleft ( -x ight )}$
2.取log
$logLleft ( mathbf{w} ight )=sum_{i=1}^{n}y^{left ( i ight )}logleft ( sigma left ( mathbf{w}^Tmathbf{x}^{left ( i ight )} ight ) ight )+left ( 1-y^{left ( i ight )} ight )logleft ( 1-sigma left ( mathbf{w}^Tmathbf{x}^{left ( i ight )} ight ) ight )$
3.需要求解的是使得log似然取得最大值的w。将其改变为最小值
$underset{mathbf{w}}{min}sum_{i=1}^{n}logleft { 1+expleft ( -y^{left ( i ight )}mathbf{w}^Tmathbf{x}^{left ( i ight )} ight ) ight }$
逻辑回归最后得到的目标式(不是最小二乘):
$J( heta) = - frac{1}{m} sum_{i=1}^m left [ y^{(i)} log h_{ heta}(x^{(i)}) + (1-y^{(i)}) log(1-h_{ heta}(x^{(i)})) ight ]$
2.平方损失函数(最小二乘法)
$L(Y, f(X)) = (Y - f(X))^2$
当样本个数为n时,此时的损失函数变为:
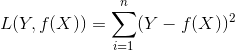
Y-f(X)表示的是残差,整个式子表示的是残差的平方和.
而在实际应用中,通常会使用均方差(MSE)作为一项衡量指标:
$MSE = frac{1}{n} sum_{i=1} ^{n} ( ilde{Y_i} - Y_i )^2$
最小二乘法是线性回归的一种,将问题转化成了一个凸优化问题。在线性回归中,它假设样本和噪声都服从高斯分布.
基本原则是:最优拟合直线应该是使各点到回归直线的距离和最小的直线,即平方和最小。换言之,OLS是基于距离的,而这个距离就是我们用的最多的欧几里得距离。
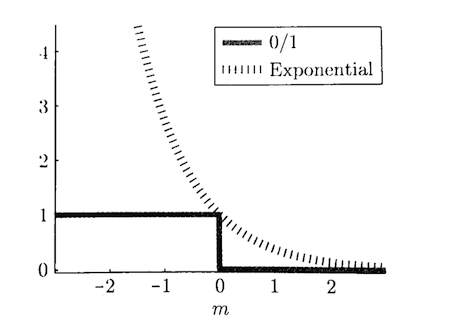
3.指数损失函数(Adaboost)
是0/1损失的一种近似
在Adaboost中,经过m此迭代之后,可以得到fm(x):
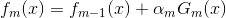
Adaboost每次迭代时的目的是为了找到最小化下列式子时的参数α 和G:
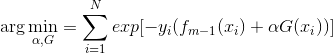
而指数损失函数(exp-loss)的标准形式如下:
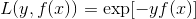
Adaboost的目标式子就是指数损失,在给定n个样本的情况下,Adaboost的损失函数为:
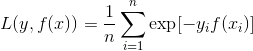
4.Hinge损失函数(SVM:合页损失)
Hinge损失是0-1损失函数的一种代理函数,Hinge损失的具体形式如下:
$maxleft ( 0,1-m ight )$
在线性支持向量机中,最优化问题可以等价于下列式子:
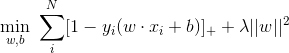
下面来对式子做个变形,令:

于是,原式就变成了:
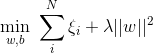
如若取λ=1/2C,式子就可以表示成:
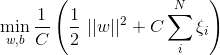
可以看出,该式子与下式非常相似:
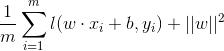
前半部分中的l就是hinge损失函数,而后面相当于L2正则项。
5.0-1损失函数
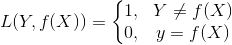
6.绝对值损失函数
![]()
梯度下降法(Gradient descent)
一个一阶最优化算法,通常也称为最速下降法。 分别有梯度下降法,批梯度下降法,增量梯度下降。本质上,都是偏导数,步长/最佳学习率,更新,收敛的问题。
目的:要使用梯度下降法找到一个函数的局部极小值,(在凸函数中局部最小解就是全局最小解)
算法流程:
1.初始化θ(随机初始化)
2.迭代,新的θ能够使得J(θ)更小
3.如果J(θ)无法继续减少或者达到循环上界次数,退出
 α:学习率、步长
α:学习率、步长

过程:
1.xk=a,沿着负梯度方向,移动到xk+1=b,有:
![]()
2.从x0为出发点,每次沿着当前函数梯度反方向移动一定距离αk,得到序列:
![]()
3.对应的各点函数值序列之间的关系为:
![]()
4.当n 达到一定值时,函数f(x)收敛到局部最小值:
学习率:
1.固定学习率
2.线性搜索
a.二分线性搜索
b.回溯线性搜索
牛顿法(改变搜索方向)
若f(x)二阶导连续,将f(x)在xk处Taylor展开:
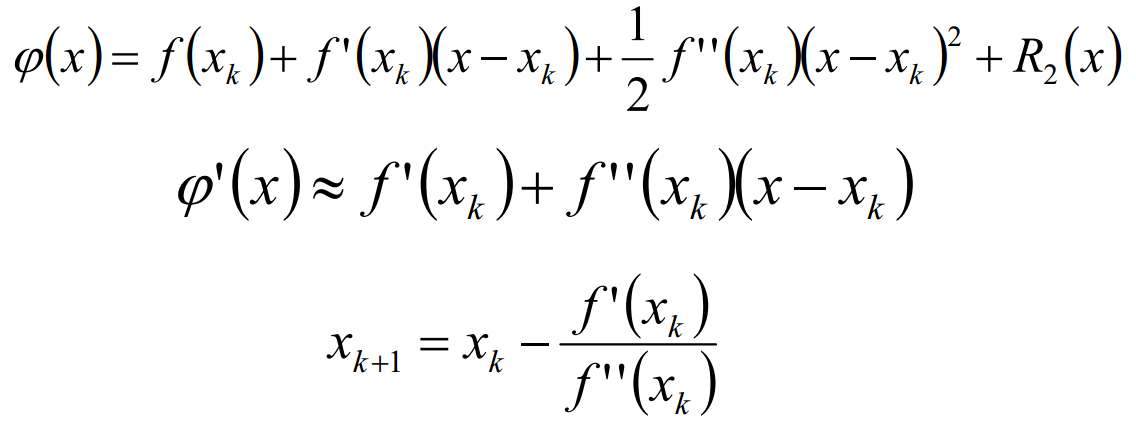
牛顿法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根。因为函数 二阶导数反应了函数的凸凹性;二阶导越大,一阶导的变化越大。用方向导数代替一阶导,用Hessian矩阵代替二阶导:
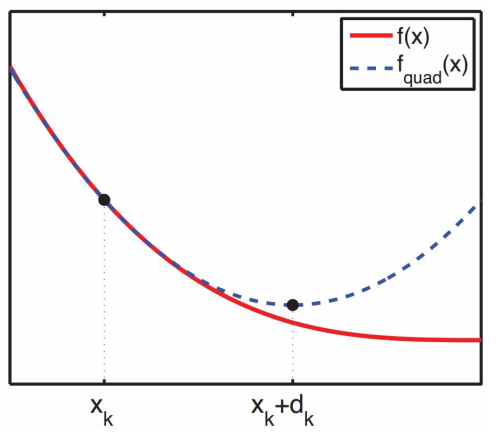
过程:
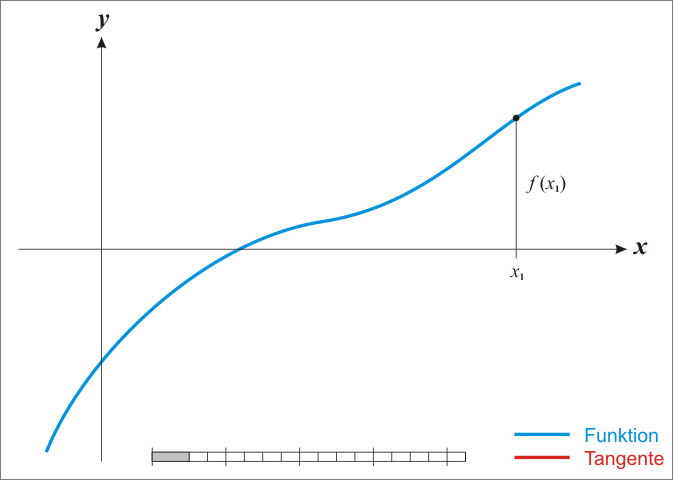
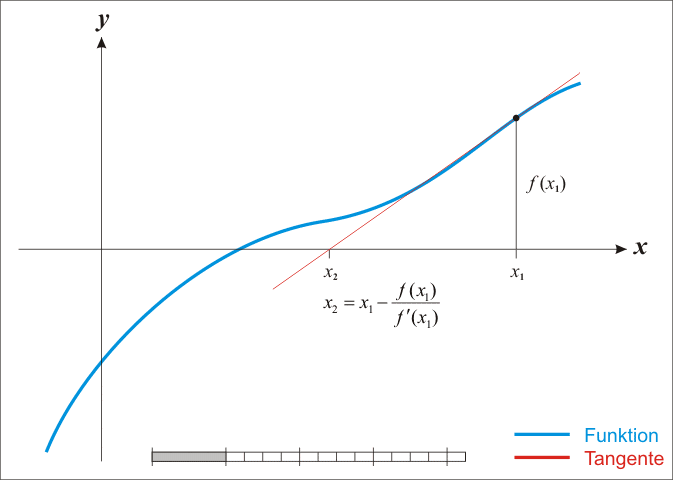
1.首先,选择一个接近函数f(x)零点的x0,计算相应的f(x0)和切线斜率f'(x0)(这里f'表示函数f的导数)。
2.然后我们计算穿过点 (x0,f(x0))并且斜率为 f'(x0)的直线和x轴的交点的x坐标,也就是求如下方程的解:
![]()
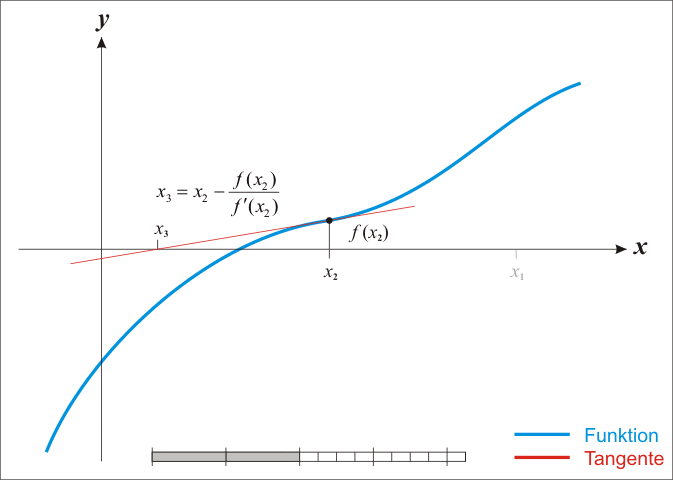
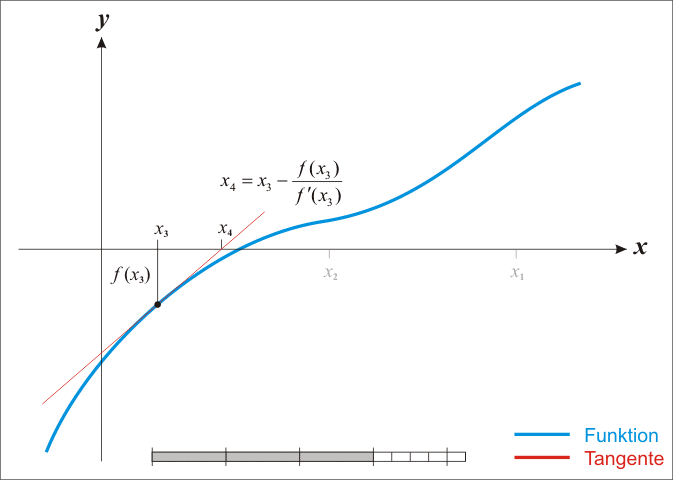
3.我们将新求得的点的x坐标命名为x1,通常x1会比x0更接近方程f(x)=0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示:
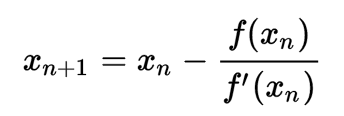
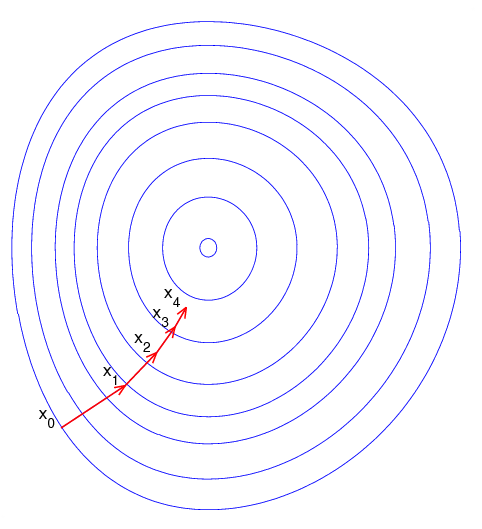
图演示:
蓝线表示方程f而红线表示切线. 可以看出xn+1比xn更靠近f所要求的根x.
牛顿法特点:
1.经典牛顿法虽然具有二次收敛性,但是要求初始点需要尽量靠近极小点,否则有可能不收敛。
2.计算过程中需要计算目标函数的二阶偏导数,难度较大。
3.目标函数的Hessian矩阵无法保持正定,会导致算法
4.产生的方向不能保证是f在xk处的下降方向,从而令牛顿法失效.
5.如果Hessian矩阵奇异,牛顿方向可能根本是不存在的。