简单的线性回归算法举例
引子
小学的时候老师出过的一道题，方程 y = w0 + w1x ，已知两组数据，求解w0和w1
x = 1 ，y = 2
x = 2 ，y = 3
两点确定一条直线，此时可以准确求得w0 和 w1
但是如果给了3组数据，可不可以准确求得w0 和 w1呢
x = 1 ，y = 2
x = 2 ，y = 3
x = 3 ，y = 5
由于这3点不在一条直线，所以不能准确求得w0 和 w1。这其实是一道错题，老师会让随便去掉一组数据求解。
这道错题其实是一个机器学习问题。我们是否可以找到一条完美直线，使得误差最小呢？
如果数据量更大，给了3亿组x和y的数据，不在一条直线上，是否能找到一条完美直线，使得误差最小呢？
从这3亿组数据找到规律的过程就是机器学习，规律就是w参数。
完美直线的定义：空间的点到直线的距离最近。不是穿过的点最多。
如何使得空间的点到直线的距离最近？
1、量化公式
有一个量化公式衡量了总误差，假设一共有m个点(xi,yi)，i = 1,2,3 ... ... m，拟合的直线的方程为 hθ(x) = w0 + w1x，
那么该量化公式为：
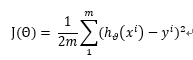
公式含义解释：
分母中的2，是为了方便求导
分母中的m是为了衡量m个点的平均距离
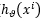是指将xi 代入到拟合的直线方程中得到的值
求平方是因为要考虑的是差值，排除负数的影响，为什么不用绝对值排除负数的影响呢？
上述公式表示将m个点的直线方程计算出的y值与实际的y的差值的平方求和，除以2m，可以衡量m个点到拟合直线的平均误差
2、 虚晃一枪：求导让导数为0
至此问题转化为求J(θ)的极小值，为了使得量化公式J(θ)越小越好，首先需要确认J(θ)是否有极小值
如果J(θ)是凹函数，就有极小值，我们可以推导出来J(θ)确实是凹函数，以下是推导过程
我们已知y = x2 是凹函数，y = kx2 + b , k>0 也是凹函数。
W为包含w0,w1两个值的列向量，X (1;x) 也是一个列向量 那么可知 W的转置 乘以X 等于 w0+w1x
则
？
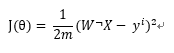
凹函数有极小值，可以通过对w0和w1求导，使导数等于0的方法求极小值
w(w0,w1) 与J的图像如下
对w0和w1分别求偏导，令导数为0 ，求解w参数
w0的偏导的求解过程如下
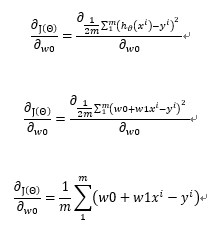
w1的偏导的求解过程如下
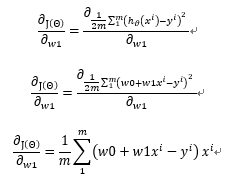
至此我们终于把导数求出来了
但是在实际情况下，上述方式不可行。海量数据下，x特别多（x1,x2,x3......），通过偏导为零反推求解 w参数，基本不可能，需要很多的算力
3、反推不行正向试
其他方法？
反推不行，正向试
随机给w参数，和 3亿组数据，代到 J(θ) 中，求得误差值，J(θ)也称为误差函数、损失函数、目标函数、最小二乘法
误差值不可能为0，因为3亿组数据不在一条直线上
人为设置一个能够容忍的误差值，比如0.01，不断迭代调整w参数，当误差值小于0.01，此时的w参数就认为是最佳参数，此时的直线是最佳直线
设置两个条件作为迭代的停止条件
迭代次数
误差阈值
当这两个条件达到其一，就停止迭代
训练模型的步骤可以概括为下述几步
1、随机w0,w1参数值
2、训练集数据和随机出来的w参数误差函数中求解出误差
3、如果误差小于用户设置的误差阈值，此时的w参数就是最佳参数
4、否则继续调整w参数，循环2 3步，直到满足停止迭代的条件为止
求解出w参数后，模型训练完毕，
当未来有了x值，求得的y值就是预测的值
迭代次数和误差阈值需要人为设置，误差阈值不是越小越好，如果误差非常小，模型可能过拟合
参数策略，调参工程师
为什么求得的误差是点到直线在y方向上的误差，而不是点到直线的垂直距离？
为什么求得的误差是点到直线在y方向上的误差
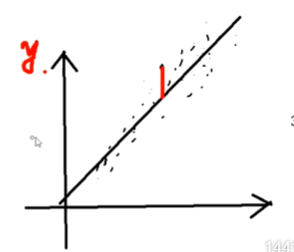
为什么不求点到直线的垂直距离
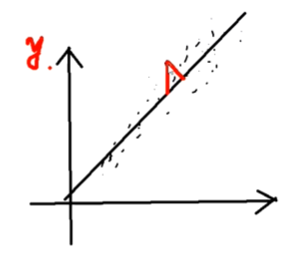
因为是要预测的y值更精准，所以是在y方向上的误差