Floyd 和 bellman 算法

Floyd-Warshall算法（Floyd-Warshall algorithm）是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。

Floyd-Warshall算法的时间复杂度为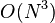 $O(N^3)$ ，空间复杂度为 $O(N^2)$ 。

原理

Floyd-Warshall算法的原理是动态规划。

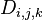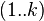设 $D_{i,j,k}$ 为从 $i$ 到 $j$ 的只以 $(1..k)$ 集合中的节点为中间节点的最短路径的长度。

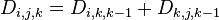若最短路径经过点k，则 $D_{i,j,k}=D_{i,k,k-1}+D_{k,j,k-1}$ ；
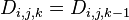若最短路径不经过点k，则 $D_{i,j,k}=D_{i,j,k-1}$ 。

因此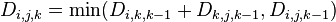， $D_{i,j,k}=mbox{min}(D_{i,k,k-1}+D_{k,j,k-1},D_{i,j,k-1})$ 。

在实际算法中，为了节约空间，可以直接在原来空间上进行迭代，这样空间可降至二维。（见下面的算法描述）

算法描述

Floyd-Warshall算法的描述如下：

for k ← 1 to n do
  for i ← 1 to n do
    for j ← 1 to n do
      if (D_{i,k} + D_{k,j} < D_{i,j}) then
        D_{i,j} ← D_{i,k} + D_{k,j};

其中 $D_{i,j}$ 表示由点 $i$ 到点 $j$ 的代价，当 $D_{i,j}$ 为 ∞ 表示两点之间没有任何连接。

Floyd-warshall 算法总结

1. 初始化时, 将 dp[i][i] 设置为 0

2. i, j 均从 1 开始遍历

3. 从状态转移方程到代码的实现, 最关键的一步是确定最外层的循环变量是谁, 而最外层的循环变量又是从状态转移方程本身推出. 比如在 Floyd 算法中, 状态转移方程是

当 k 在最短路径上时, dp(i, j, k) = dp(i, k, k-1) + dp(k, j, k-1)

当 k 不在最短路径时, dp(i, j, k) = dp(i, j, k-1)

可以转化为 g(k) = f(k, k-1), 因此应该把 k 作为最外层的循环变量

4. 空间压缩. 在求解 dp(i, j, k) 时, 会用到 dp(i, k, k-1) 和 dp(k, j, k-1) 以及 dp(i, j, k-1). 新生成的数据 dp(i, j, k) j != k 不会被重复利用, 因此可以使用二维空间

Bellmanford 算法

1. 与 Dijsktra 算法的比较. D 是一种贪心算法, 贪心策略为选取未被处理的最短的节点, 理由是该节点有潜力更新某些节点的距离, 使之变得更小, 每次对该节点的出边进行松弛. 而 B 算法简单的对所有的边进行松弛, 可以看出, D 算法进行的运算是 B 算法的子集. B 算法的优点是不仅可以处理负权边, 还能判断图是否存在负环.

2. 松弛. 松弛实际上是对相邻节点的访问, 第 n 次松弛保证了保证了所有深度为 n 个节点得出了最短路径. 由于图最短路径最深至多是 V-1, 因此 V-1 次松弛即可确定所有点的最短路径

3. 负权环判定. 因为负权环可以无限制的拉低最短路径, 因此在进行第 V 次松弛后, 最短路径值有所减小, 那么可以肯定, 存在负权环

4. 朴素 BellmanFord 算法

procedure BellmanFord(list vertices, list edges, vertex source)
   // 该实现读入边和节点的列表，并向两个数组（distance和predecessor）中写入最短路径信息

   // 步骤1：初始化图
   for each vertex v in vertices:
       if v is source then distance[v] := 0
       else distance[v] := infinity
       predecessor[v] := null

   // 步骤2：重复对每一条边进行松弛操作
   for i from 1 to size(vertices)-1:
       for each edge (u, v) with weight w in edges:
           if distance[u] + w < distance[v]:
               distance[v] := distance[u] + w
               predecessor[v] := u

   // 步骤3：检查负权环
   for each edge (u, v) with weight w in edges:
       if distance[u] + w < distance[v]:
           error "图包含了负权环"

5. SPFA 优化

SPFA 是 Shorest Path Faster Algorithm 的简写. SPFA 基于一个事实: 松弛有效的操作必然发生在松弛的前导节点成功松弛的节点上.

用一个队列记录松弛过的节点, 可以减少冗余计算, 将复杂度降低到 o(kE)

Begin
  initialize-single-source(G,s);
  initialize-queue(Q);
  enqueue(Q,s);
  while not empty(Q) do 
    begin
      u:=dequeue(Q);
      for each v∈adj[u] do 
        begin
          tmp:=d[v];
          relax(u,v);
          if (tmp<>d[v]) and (not v in Q) then
            enqueue(Q,v);
        end;
    end;
End;