一、 扯淡
转眼间毕业快一年了，这期间混了两份工作，从游戏开发到算法。感觉自己还是喜欢算法，可能是大学混了几年算法吧！所以不想浪费基础。。。
我是个懒得写博客的人，混了几年coding，写的博客不超过10篇。现在参加工作，必须得改掉懒的坏习惯，以后多尝试写写，好总结总结，也方便以后复习用。
二、算法
1. 前言
1.1 EM会涉及一些数学知识，比如最大似然估计和Jensen不等式等知识，这些知识最烦了，动不动就一堆推导公式，看着就觉得蛋疼，经过它讲的原理比较简单，多以在此略过。
1.2 本文的侧重点是理解EM，试图以“数形结合”的方式来帮助大家理解其原理。（因为博主看了很多相关的文章，大多是一堆数学公式，看了半天也不好理解，虽然感觉是这个样子）。
2. 算法描述
给定样本T = {X1, X2, …， Xm}，现在想给每个Xi一个Zi，即标出： {(X1,Z1), (X2,Z2),…，(Xm,Zm)}（z是隐形变量，zi=j可以看成是Xi被划分为j类），求对T的最大似然估计：
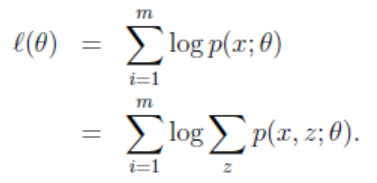
其实Zi也是个向量，因为对于每一个Xi，都有多种分类的情况。设第i个样本Xi在Z上的概率分布为Qi(Zi)，即Qi(Zi=j)表示Xi被划分到类j的概率，因此有ΣQi(Zi) = 1。
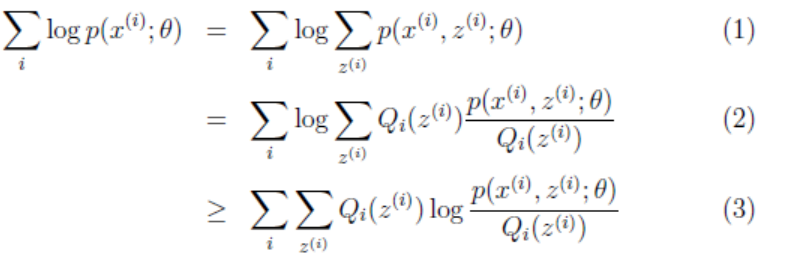
(2)到(3)是利用Jensen不等式，因为log(x)为凹函数，且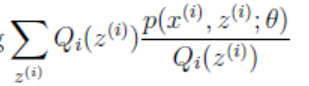
这个就是p（xi, zi; θ）/Qi(zi)的期望。
现在，根据Jensen不等式取等号的条件：
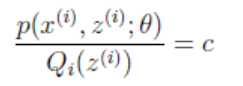
因为这个式子对于Zi等于任何值时都成立，且有ΣQi(Zi) = 1，所以可以认为：Σp(xi, zi;θ) = c。此时可以推出：
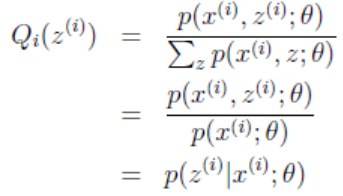
式子中，Zi是自变量，若θ已知，则可计算出Qi(zi)。
至此，终于可以描述算法过程了：
1）给θ一个初始值；
2）固定当前的θ，让不等式(3)取等号，算出Qi(zi)；-------> E 步
3）将2）算出的Qi(zi)代入g(Q, θ) =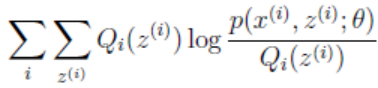 
，并极大化g(Q，θ)，得到新的θ。-------------->M步
4）循环迭代2）、3）至收敛。
3. 证明算法的收敛
1）首先我们知道上节所提到的g(Q,θ)为最大似然函数L(θ)的下界函数，也就是说，无论Q、θ怎么变，g永远在L下面；
2）函数L(θ)是关于θ的函数，z是从θ抽离的隐含变量，其实它也是关于θ的函数；
3）g(Q,θ)是关于Q、θ的函数，但我们可以看做是θ的函数，而Q只是控制函数图像的，例如：f(x) = a*x^2 +1 ,虽然a、x都是可变的，但是为了画图，我们把f(x)看做x的函数。
有了以上前提，我们就能画出它们的关系：
如上图，描述了EM的迭代过程:（z代替了公式中的Q）
1）起始状态θ0， z0，则函数g(z,θ)看成是g_z0(θ);
2）θ=θ0不变，让不等式3）取等号，即z由z0变为z1，此时让g_z1(θ) 相切于点P1，因为此时不等式取等号：L(θ0)=g_z1(θ0);--------------->E步
3）p1不一定是g_z1的极值点，因此求得极值点M1（常规方法：求导=0）；---------------->M步
4）依据2）中的方法，再次调整z，得到函数g_z2(θ)，是其于L(θ)相切于p2;------------------>E步
5）p2不一定是函数g_z2(θ)的极值点（因为函数g的图像改变了，g_z1->g_z2），因此再对g_z2(θ)求极值点M2;-------------------->M步
……
n）迭代至g_zn(θn-1)与L(θ)区部极值点非常接近为止。
由以上得，EM算法可以逼近L(θ)的极值点，但可能是局部极值点，因此要改变初始值，执行多次。
EM的数学证明也很简单，可以参照以下博客：http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html
其中包含了jensen不等式的证明。
PS：个人思路，不对的地方还请指出，我会及时改进，谢谢！