@
1.坐标空间
我们在以前渲染流水线中就接触了坐标空间的变换。例如,在学习顶点着色器流水线阶段时,我们说过,顶点着色器的最基本功能就是把模型的顶点坐标从模型空间转换到齐次裁剪坐标空间中。
1.2 坐标空间的变换
我们先要为后面的内容做些数学铺垫。在渲染流水线中,我们往往需要把一个点或方向矢量从一个坐标空间转换到另一个坐标空间。这个过程到底是怎么实现的?
我们把问题一般化,我们知道,要想定义一个坐标空间,必须指明其原点的位置和三个坐标轴的方向。而这些数值实际上是相对于另一个坐标空间的(读者需要记住,所有的都是相对的)。也就是说,坐标空间会形成一个层次结构——每个坐标空间都是另一个坐标空间的子空间,反过来说,每个空间都有一个父(parent)坐标空间。对坐标空间的变换实际上就是在父空间和子空间之间对点和矢量进行变换。
假设现在有父坐标空间P以及一个子坐标空间C。我们知道父坐标空间中子坐标空间的原点位置以及3个单位坐标轴。我们一般会有两种需求:一种需求是把子坐标空间下表示的点或矢量Ac转换到父坐标空间下的表示Ap,另一个需求是反过来,即把父坐标空间下表示的点或矢量Bp转换到子坐标空间下的表示Bc。我们可以通过下面的公式来表示这两种需求:
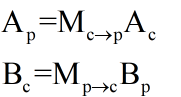
其中,Mc->p表示的是从子空间转换到父空间的变换矩阵,而Mp->c是其逆矩阵(即反向变换)。那么现在的问题是,如何求解这些变换矩阵?事实上,我们只要求出二者之一即可,另一个矩阵可以通过求逆矩阵的方式来得到。
下面,我们来讲解如何来求出从子坐标空间到父坐标空间的变换矩阵Mc->p。
首先,我们来回顾一个看似很简单的问题:当给定一个坐标空间以及其中一点(a,b,c)时,我们是如何知道该点的位置呢?我们可以通过四个步骤来确定它的位置。
(1)从坐标原点开始
(2)向x轴方向移动a个单位
(3)向y轴方向移动b个单位
(4)向z轴方向移动c个单位
需要说明的是,上面的步骤只是我们的想象,这个点实际没有发生移动。上面的步骤看起来再简单不过了,坐标空间的变换就蕴含在上面的4个步骤中。现在,我们已知坐标空间C的三个坐标轴在父坐标空间P下的表示Xc,Yc,Zc,以及原来的原点Oc。当给定一个子坐标空间中的一点Ac=(a,b,c),我们同样可以依照上面4个步骤来确定其在父坐标空间下的位置Ap:
(1)从坐标的原点开始
这很简单,我们已经知道了子坐标空间的原点位置Oc。
(2)向x轴方向移动a个单位
仍然很简单,因为我们已经知道了x轴的矢量表示,因此可以得到
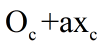
(3)向y轴方向平移b个单位
同样的道理,这一步就是:
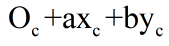
(4)向z轴方向平移c个单位
最后就可以得到
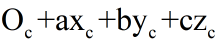
现在,我们已经求出了Mc->p!什么?你没看出来吗?我们再来看一下最后得出的式子:
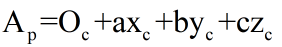
你们可能会问,这个式子里根本没有矩阵啊!其实,我么我们只要稍微使用一点魔法,矩阵就会出现在上面的式子中:

其中“|”符号表示是按列展开的。上面式子实际上就是使用了我们之前所学的数学公式而已。但这个最后的表达式还不是很漂亮,因为还存在加法表达式,即平移变换。我们已经知道了3×3矩阵无法表示平移变换,因此,为了得到一个更漂亮的结果,我们把上面的式子扩展到齐次坐标空间中,得

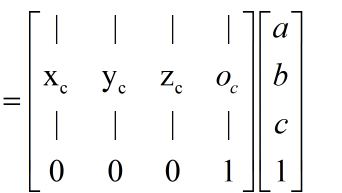
那么现在你看到Mc->p在哪里了吧,没错,

一旦求出来Mc->p,Mp->c就可以通过求逆矩阵的方式求出来,因为从坐标空间C变换到坐标空间P与从坐标空间P变换到坐标空间C是互逆的两个过程。
可以看出来,变换矩阵Mc->p实际上可以通过坐标空间C在坐标空间P中的原点和坐标轴的矢量表示构建出来:把3个坐标轴依次放入矩阵的前三列,把原点矢量放到最后一列,再用0和1填充最后一行即可。
需要注意的是,这里我们并没有要求3个坐标轴Xc、Yc和Zc是单位矢量,事实上,如果存在缩放的话,这三个矢量值很可能不是单位矢量。
更加令人振奋的是,我们可以利用反向思维,从这个变换矩阵反推来获取子坐标空间的原点和坐标轴方向。例如,当我们已知从模型空间到世界空间的一个4×4的变换矩阵,可以提取它的第一列再进行归一化后(为了消除缩放的影响)来得到模型空间的x轴在世界空间下的单位矢量表示。同样的方法也可以提取y轴和z轴。我们可以从另一个角度来理解这个提取过程。因为矩阵Mc->p可以把一个方向矢量从坐标空间C变换到坐标空间P中,那么,我们只需要用它来变换坐标空间C中的x轴(1,0,0,0),即使用矩阵乘法M->p[1 0 0 0]T,得到的结果正是Mc->p的第一列。
另一个有趣的情况是,对方向矢量的坐标空间变换。我们知道,矢量是没有位置的,因此坐标空间的原点变换是可以忽略的。也就是说,我们仅仅平移坐标系的原点是不会对矢量造成任何影响的。那么,对矢量的坐标空间变换就可以使用3×3矩阵来表示,因为我们不需要平移变换。那么变换矩阵就是:
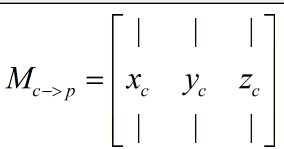
在shader中,我们常常会看到截取变换矩阵的前3行前3列来对法线方向、光照方向来进行空间变换,这正是原因所在。
现在,我们再来关注Mp->c。我们前面讲到,可以通过求Mc->p的逆矩阵方式求解出来反向变换Mp->c。但有一种情况我们不需要求解逆矩阵就可以得到Mp->c,这种情况就是Mc->p是一个正交矩阵。如果它是一个正交矩阵的话,Mc->p的逆矩阵就等于它的转置矩阵。这意味着我们不需要进行复杂的求逆操作就可以得到反向变换。也就是说,如果我们知道坐标空间变换矩阵Ma->b是一个正交矩阵,那么我们可以提取它的第一列来得到坐标空间A的x轴在坐标空间B下的表示,还可以提取它的第一行来得到坐标空间B的x轴在坐标空间A下的表示。反过来,如果我们知道坐标空间B的x轴、y轴和z轴(必须是单位矢量,否则构建出来的就不是单位矩阵了)在坐标空间A下的表示,就可以把它们依次放在矩阵的每一行就可以得到A到B的变换矩阵了。