DP&图论 DAY 4 下午
后天考试不考二分图,双联通
考拓扑排序
图论

图的基本模型

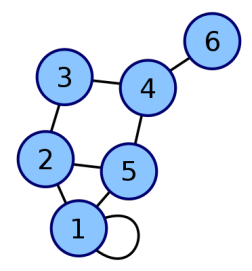
边:
有向边构成有向图
无向边构成无向图
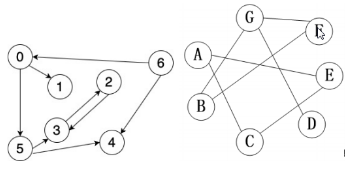
权值:
1.无权
2.点权
3.边权
4.负权(dij不可以跑)
环:
1.
2.重边
3.有向无环图DAG
路径:
1.简单路径:不经过重复的点 1-->2-->3
不简单路径:经过重复点 1-->2-->3-->1-->4
2.连通,具有传递性
图:
1.树:n个点,n-1条边的无环连通图
2.完全图:一个无向图,图中任意两点之间都有一条连边
3.竞赛图:完全图中的每一条边确定一个方向
4.基环树
5.仙人掌:不是树,图里可以成环,每一条边,要么不在环上,要么只属于一个环
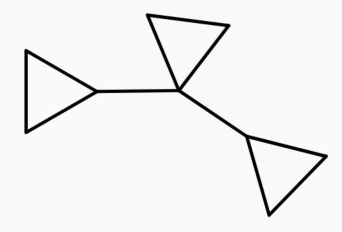
图的输入方式

图的存储方式


图的遍历方法



拓扑排序基于BFS

三种遍历顺序
1.前序遍历 中左右
2.中序遍历 左中右
3.后序遍历 左右中
QUS:给前序中序,写后序
前序第一个就是根,找到在中序的位置,递归
例题1:
给定一个有向图,边权为 1 或 2,求单源最短路。
>Solution
稍微改写一下 BFS 即可。
# 创建三个集合, Q0 表示当前层, Q1 表示距离为 1 的层,
Q2 表示距离为 2 的层,初始 Q0 = {s}, Q1= ∅, Q2= ∅
# 依次取出 Q0 中的点,将其邻点放入对应的 Q1 或 Q2 中
# Q0 = Q1, Q1 = Q2, Q2 = ∅
注意一个点可能和当前层既有长度为 1 的边,又有长度为 2 的
边,应当将其加入 Q1 而非 Q2。
bfs:
建立一个辅助点
每个权是2的边u→v ,都改成 u→辅助点,辅助点→v ,权为1 ,这样边权就都是1
例题2
给出一个有向图和起点 s,对每条边 < u, v > 回答,如果删去这
条边,从 s 到 v 的最短路长度是否会改变。
>Solution
# BFS 求出从 s 出发的单源最短路
# 建立最短路图,即保留满足 dv = du + 1 的边 < u, v >
#如果询问的边不在最短路图中,那么删掉不改变
# 在最短路图上,如果 v 的入度为 1,则该入边是从 s 到 v
的必经边,若删去则 v 的最短路长度会改变
# 在最短路图上,如果 v 的入度大于 1,则删去任何一条入
边, v 的最短路长度都不会改变
拓扑排序
有向无环图的拓扑排序即将所有顶点排为线性序列,使得对于任意的 < u, v >∈ E,都有 u 在线性序列中出现于 v 之前。
有向图中如果有环,则一定不存在拓扑排序;如果没有环,则一定存在拓扑排序。
# 选取一个入度为 0 的点记为 u
# 将 u 添加到线性序列末端
# 删去所有 u 的出边
# 重复上述步骤直到所有点都被加入序列
void topsort() { queue<int> q; for(int i=1;i<=n;i++) if(!in[i]) q.push(i); while(!q.empty()) { int u=q.front(); q.pop(); ans[++cnt]=u; for(int i=head[u];i;i=edge[i].nxt) { int y=edge[i].v; in[y]--; if(!in[y]) q.push(y); } } if(cnt!=n) printf("you fu huan!!!"); }

// Tuo Pu Pai Xu void toposort() { static int que[mxn]; int l = 0, r = 0; for (int i = 1; i <= n; ++i) if (cnt[i] == 0) que[r++] = i; while (l != r) { int u = que[l++]; for (int i = hd[u], v; i; i = nt[i]) if (--cnt[v = to[i]] == 0) que[r++] = v; } }
例题1
有 n 项任务,有 m 个限制,第 i 个限制要求执行任务 ui 之前
必须要完成任务 vi。请问是否存在合适的任务执行顺序,满足所
有的限制。
>Solution
将每个任务视为一个点,任务之间的依赖构成了有向边。如果该
有向图中没有环,则存在拓扑排序,而拓扑排序就是可行的任务
执行顺序;如果该有向图中存在环,则无解。
例 2
有 n 项任务,有 m 个限制,限制有如下两种:
# 执行 u 任务之前必须要完成 v 任务
# 存在某一时刻, u 和 v 任务都在执行
请问是否存在安排每个任务起始时间和结束时间的方案,满足所
有的限制。
>Solution
为每个任务的起始时间和结束时间各对应一个点,任务 i 的起始
时间点记为 si,结束时间点记为 ei。
# 要保证每个任务的结束时间在起始时间之后,所以对所有 i,连边 < si, ei >
# 如果要求任务 a 在任务 b 开始执行之前完成,则连边< ea, sb >
# 如果要求任务 a 和 b 在某个时刻都在执行,则连边< sa, eb >, < sb, ea >
对于上面的有向图,如果存在环则无解,否则根据其拓扑排序易构造一个方案。
例 3
对于带边权的有向无环图,求单源最短路。
>Solution

POJ 1094 Sorting It All Out
An ascending sorted sequence of distinct values is one in which
some form of a less-than operator is used to order the elements
from smallest to largest. For example, the sorted sequence A, B,
C, D implies that A < B, B < C and C < D. in this problem, we
will give you a set of relations of the form A < B and ask you to
determine whether a sorted order has been specifed or not.
由一些不同元素组成的升序序列是可以用若干个小于号将所有的
元素按从小到大的顺序 排列起来的序列。例如,排序后的序列
为 A, B, C, D,这意味着 A < B、 B < C 和 C < D。在本题中,
给定一组形如 A < B 的关系式,你的任务是判定是否存在一个
有序序列。输出到哪一项可以确定顺序或者在这一项最先出现冲
突,若所有的小于关系都处理完了都不能确定顺序也没有出现冲
突,就输出不能确定。
>Solution
# 冲突即为出现环
# 确定即为拓扑排序时队中元素不大于 1
每次取队首,队列里只有一个元素,那么顺序唯一确定
# 每次加入新的关系重新拓扑排序一次即可
BZOJ 2200 道路和航线
FJ 正在一个新的销售区域对他的牛奶销售方案进行调查。
他想把牛奶送到 T 个城镇 (1 ≤ T ≤ 25000),编号为 1 到 T。
这些城镇之间通过 R 条道路 (1 ≤ R ≤ 50000) 和 P 条航线(1 ≤ P ≤ 50000) 连接。
每条道路 i 或者航线 i 连接城镇 Ai 到Bi,花费为 Ci。
对于道路, 0 ≤ Ci ≤ 10000;
然而航线的花费很神奇,花费 Ci 可能是负数 (-10000 ≤ Ci ≤ 10000)。
道路是双向的,可以从 Ai 到 Bi,也可以从 Bi 到 Ai,花费都是 Ci。
然而航线与之不同,只可以从 Ai 到 Bi。
事实上,由于最近恐怖主义太嚣张,为了社会和谐,出台了一些政策保证:
如果有一条航线可以从 Ai 到 Bi,那么保证不可能通过一些道路和航线从 Bi 回到Ai。
由于 FJ 的奶牛世界公认〸分给力,他需要运送奶牛到每一个城镇。
他想找到从发送中心城镇 S 把奶牛送到每个城镇的最便宜的方案,或者知道这是不可能的。
>Solution
有向边不在环内,走拓扑排序
任何在环的地方,都是正权无向边,dij,把 topsort 被更新过的点扔进堆里做 dij ,(也可以直接全部所有点都扔进去)
e 
最短路算法
Floyd
# 基于动态规划, Fk,u,v, 表示使用点 1, 2, . . . , k 时,点 u 到点 v 的最短路
限制中间点前 k 个
# 从小到大枚举 k, u 和 v 之间的最短路要么不经过 k,要么经过 k 一次且除此之外只包含前 k - 1 个点
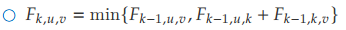
易见,使用二维数组不断覆盖更新即可。
时间复杂度 O(N3)
空间复杂度 O(N2)
可以处理含有负权边的情况,如果含有负环,则存在 i 使得Fi,i < 0。

出现负环,f[i][i] < 0
Floyd 传递闭包,图中任意两点的可达性
如果 i-->k , k->j ,可达,那就更新

玄学剪枝

邻接矩阵初始化
快速幂
Floyd具有矩阵乘法的一些性质,Floyd具有结合律
Dijkstra
适用于没有负权边的图。
# 将所有点分为两个集合,最短路确定的集合 S 和最短路未确定的集合 T,初始 S = {s}
# 求 T 中每个点 v 的当前最短路
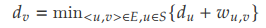
# 取出 T 中 dv 最小的点,其最短路一定就是 dv,将其加入 S
# 不断重复上面的操作,直到所有点的最短路都确定
朴素写法时间复杂度较劣,可以采用堆优化至 O((N + M) logN)
>下面是C++11 的写法

下面是个C++98 的写法
// Dijkstra Template (without c++11) struct data { int u; int d; data(int _u, int _d) : u(_u), d(_d) {} bool operator < (const data & that) const { return d > that.d; }//注释1 }; priority_queue<data> heap;
const int inf=0x3f3f3f3f;
void dijkstra(int s) { memset(dis, inf, sizeof dis); heap.push(data(s, dis[s] = 0)); while (!heap.empty()) { data t = heap.top(); heap.pop(); if (t.d != dis[t.u])continue; //注释2 for (int i = hd[t.u], v, w; i; i = nt[i]) if (v = to[i], w = vl[i], dis[v] > t.d + w)
//,表达式,最后一个作为返回值 heap.push(data(v, dis[v] = t.d + w)); } }
注释1:
就是重载一个小于号然后按照d从大到小排序
const保险还是加上
注释2:

此处是为了判断点 t.u 有没有更新过别人,更新过就没必要多次更新了
因为你从堆里面取出一个点,用他来更新别的点的最短距离,那么就说明他的最短路径已经被更新过了,是最小的dis[t.u]了
然后对于一个点 v ,他会被别的点更新 dis[v] , 可能原来的dis[v]不是最优的,但是他被加到堆里面了,然后后面出现一个更新的新的dis[v],然后再次更新dis[v]
但是注意priority_queue不支持修改操作,就是对于点 v ,你无法修改他在堆里那个 pair.second ,你只能新建一个data类型的东西,塞到堆里
这样的话,取出 v 来更新别的点的 dis ,那么可能会出现取出原来本应该删除但是由于pq不支持删除而留下的错误dis ,为了防止错误答案更新错误答案,判断一下!!!,如果是个错误答案直接continue掉
Bellman-Ford

// Bellman-Ford struct edge { int u, v, w; edge(int _u, int _v, int _w) : u(_u), v(_v), w(_w) {} } e[mxm]; void bellman_ford(int s) { memset(dis, inf, sizeof dis); dis[s] = 0; int cnt = 0, flag = 1; while (flag) { flag = 0; for (int i = 0; i < m; ++i) if (dis[e[i].v] > dis[e[i].u] + e[i].w) dis[e[i].v] = dis[e[i].u] + e[i].w, flag = 1; } if (++cnt > n) you_fu_huan!!!! break; }
SPFA
考虑使用队列优化 Bellman-Ford 算法,如果更新了 du,则将 u 入队。每次取队首 u 更新其邻点 v 的 dv。
最坏复杂度 O(NM)
void spfa() { for(int i=1;i<=n;i++) { dis[i]=inf;vis[i]=0; } dis[s]=0; vis[s]=1; q.push(s); while(!q.empty()) { int u=q.front(); q.pop(); vis[u]=0; for(int i=head[u];i;i=edge[i].next) { int v=edge[i].to; if(dis[v]>dis[u]+edge[i].dis) { dis[v]=dis[u]+edge[i].dis; if(!vis[v]){ q.push(v); vis[v]=1; } } } } }
判断有没有负环就是,如果一个点入队的次数>n次,那么就说明出现了负环,开个数组记录一下

// SPFA void spfa(int s) { memset(dis, inf, sizeof dis); static int que[10000000]; static bool vis[mxn]; int l = 0, r = 0; dis[que[r++] = s] = 0; while (l != r) { int u = que[l++]; vis[u] = false; for (int i = hd[u], v, w; i; i = nt[i]) if (v = to[i], w = vl[i], dis[v] > dis[u] + w) if (dis[v] = dis[u] + w, !vis[v]) vis[que[r++] = v] = true; } }
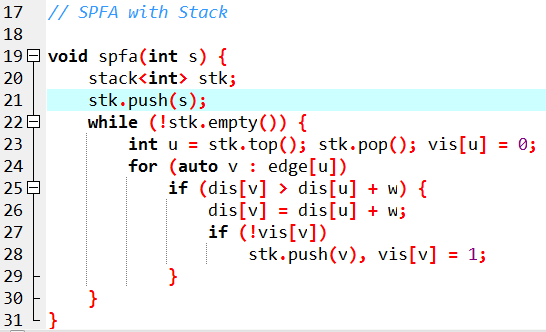
栈更容易判负环
