50. Pow(x, n)

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000
示例 2：

输入：x = 2.10000, n = 3
输出：9.26100
示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

解法一：暴力求解

public double myPow(double x, int n) {
        double sumx = 1;
        for (int i = 1; i <= n; i++)
            sumx *= x;
        return sumx;
    }

时间复杂度：O（N)

空间复杂度：O（1）

解法二：暴力求解是自下而上的，所以容易造成数据的撑死，但是第二种方法是通过自上而下构造的

 public double myPow(double x, int n) {
        if (n < 0) {
            return 1.0 / recPow(x, n *= -1);
        } else if (n > 0) {
            return recPow(x, n);
        }
        return 1.0;
    }

    double recPow(double x, int n) {
        if (n == 0)
            return 1;
        double y = recPow(x,n/2);
        return n%2==0?y*y:y*y*x;
    }

时间复杂度：O(N)

空间复杂度：O(1)

解法三：牛顿迭代法

牛顿迭代法快速寻找平方根

    下面这种方法可以很有效地求出根号a的近似值：首先随便猜一个近似值x，然后不断令x等于x和a/x的平均数，迭代个六七次后x的值就已经相当精确了。
    例如，我想求根号2等于多少。假如我猜测的结果为4，虽然错的离谱，但你可以看到使用牛顿迭代法后这个值很快就趋近于根号2了：

(       4  + 2/   4     ) / 2 = 2.25
(    2.25  + 2/   2.25  ) / 2 = 1.56944..
( 1.56944..+ 2/1.56944..) / 2 = 1.42189..
( 1.42189..+ 2/1.42189..) / 2 = 1.41423..
….

       
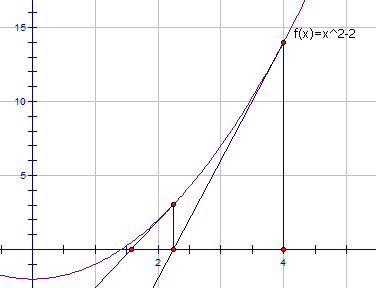
    这种算法的原理很简单，我们仅仅是不断用(x,f(x))的切线来逼近方程x^2-a=0的根。根号a实际上就是x^2-a=0的一个正实根，这个函数的导数是2x。也就是说，函数上任一点(x,f(x))处的切线斜率是2x。那么，x-f(x)/(2x)就是一个比x更接近的近似值。代入f(x)=x^2-a得到x-(x^2-a)/(2x)，也就是(x+a/x)/2。
    同样的方法可以用在其它的近似值计算中。Quake III的源码中有一段非常牛B的开方取倒函数。

int mysqrt(int x){
    double tmpx = x;
    double k = 1.0;
    double k0 = 0.0;
    while(abs(k0-k) >= 1){
        k0 = k;
        k = (k + tmpx/k)/2;
    }
    return (int)k;
}