对于傅里叶的各种推倒证明这里不提,本文着重‘看公式写代码’。
一维离散福利叶变换的公式:
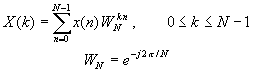
反傅里叶:
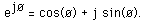
/*
函数:FFT2
功能:(反)傅里叶变换 --- 基2
参数:ptd -- in 空域
pfd -- out 频域
nlevel --- in 步数
sign --- 1 反傅里叶 -1 傅里叶
*/
void FFT2(complex *pTd , complex * pFd , int nlevel,int sign)
{
int nLength = pow(2.0,1.0*nlevel);
complex * pw = (complex * )malloc(nLength * sizeof(complex));
for (int i = 0 ; i <nLength ; ++i)
{
pw[i].real = 0.0 ;
pw[i].image = 0.0;
}
double angle = 0.0;
for (int i = 0 ; i < nLength ;++i)
{
for (int j = 0 ; j < nLength ; ++j)
{
angle = 2.0*CV_PI * i * j* sign / nLength ;
pFd[i]+=(complex(cos(angle) , sin(angle)) *pTd[j]);
}
}
if (sign == 1)
{
for (int i = 0 ; i < nLength ; ++i)
pFd[i]/=nLength;
}
free(pw);
}
函数:FFT2
功能:(反)傅里叶变换 --- 基2
参数:ptd -- in 空域
pfd -- out 频域
nlevel --- in 步数
sign --- 1 反傅里叶 -1 傅里叶
*/
void FFT2(complex *pTd , complex * pFd , int nlevel,int sign)
{
int nLength = pow(2.0,1.0*nlevel);
complex * pw = (complex * )malloc(nLength * sizeof(complex));
for (int i = 0 ; i <nLength ; ++i)
{
pw[i].real = 0.0 ;
pw[i].image = 0.0;
}
double angle = 0.0;
for (int i = 0 ; i < nLength ;++i)
{
for (int j = 0 ; j < nLength ; ++j)
{
angle = 2.0*CV_PI * i * j* sign / nLength ;
pFd[i]+=(complex(cos(angle) , sin(angle)) *pTd[j]);
}
}
if (sign == 1)
{
for (int i = 0 ; i < nLength ; ++i)
pFd[i]/=nLength;
}
free(pw);
}
上述算法(DFT)的复杂度为 N * N (N个点每个点的变换都有N点参与运算),而基2快速傅里叶变换(FFT)则降低了复杂度达到 N * log
(N)/log(2)(N个点每个点的变换有log(N)/log(2)个点参与运算),主要是利用傅里叶公式的周期性 对称性减少了重复计算,具体推导参考
相关书籍,网上大多有对FFT的推导或者直接给出代码,本文主要对代码解释。
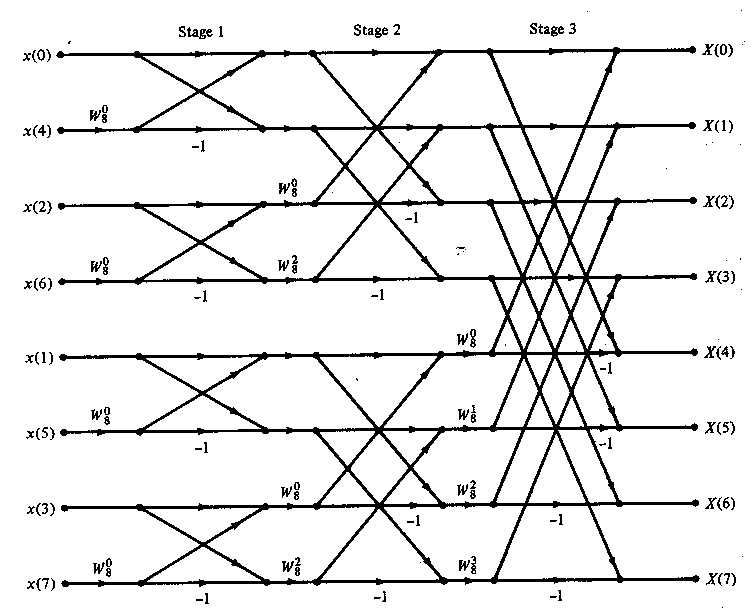

1.位变换
从上图1看出 x0(000) -- 变换后为x0(000) x1(001)---x4(100) x2(010)---x2(010)等等
位变换的意思是 比如 1100 变换后为 0011 ,通俗的理解就是 1100 从左往右开始对应1的位置 ,变换成 从右往左为对应位置为1(0011)
2.蝶形运算
如何来的:
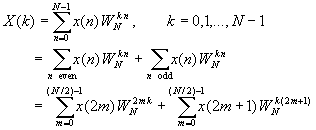

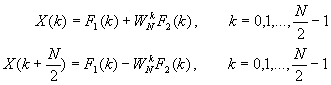
别别看上面的推导了,晕忽忽的~~ ,总之就是各种对称性 周期性以后成了最后的样子
如果以F1(K),F2(K)为最终运算的话那就错了,对应公式中来看F1(K),F2(K)的计算还是要有其他点做贡献的,所以要对F1(K),F2(K)再分解一
一直到不能分解为止,图1是 N=8的分解情况及对应关系。
这里提出三个辅助名词 :级数level 跨度间隔B 加权系数P
图1:
总数为8 level = log(8)/log(2) = 3
B=1,2,4 每一级增加一倍
P=0 , 0 2 , 0 1 2 3 每一级增加一倍
图2:
总数为16 level = log(16)/log(2) = 4
B=1,2,4,8 每一级增加一倍
P=0 , 0 4 , 0 2 4,6, 0 1 2 3 4 5 6 7 每一级增加一倍
依次类推....................好吧从这里找规律,下面代码就是这么来的。
void FFT(complex *pTd , complex * pFd , int nlevel,int sign)
{
//nLength = 2 ^nlevel
int nLength = pow(2.0,1.0*nlevel);
//求W = e ^(-j*2*PI/nlength) = cos(-2*PI/nlength) + j*sin(-2*PI/nlength)
complex *pw = (complex *)malloc(nLength *sizeof(complex)/2);
double angle = 0.0;
for (int i = 0 ; i <nLength/2 ;++i)
{
angle =CV_PI *sign *2.0 * i /nLength ;
pw[i] = complex(cos(angle),sin(angle));
}
//位变换
int p = 0 ;
for (int i = 0 ; i <nLength ;++i)
{
p = 0 ;
for (int j = 0 ; j <nlevel ; ++j)
{
if (i & (1<< j) )
p+=1<<(nlevel - j -1);
}
pFd[p] = pTd[i];
}
//蝶形算法
int B=0; //跨度间隔
int weight = 0 ; //加权系数
complex *x1 = (complex *)malloc(nLength * sizeof(complex));
for (int i = 0 ; i <nlevel ; ++i)
{
B = 1<<i; //跨度间隔 1 ,2 ,4 ,8 ..............
for (int j =0 ; j <B; ++j)
{
weight = (1<<(nlevel - i -1)) * j;
for (int k = j ; k <nLength ; k+=(1<<(i+1)))
{
x1[k] = pFd[k] + pFd[k+B] * pw[weight];
x1[k+B] = pFd[k] - pFd[k+B]*pw[weight];
}
}
memcpy(pFd,x1,nLength * sizeof(complex));
}
if (sign == 1)
{
for (int i = 0 ; i < nLength ; ++i)
pFd[i]/=nLength;
}
free(pw);
free(x1);
}
{
//nLength = 2 ^nlevel
int nLength = pow(2.0,1.0*nlevel);
//求W = e ^(-j*2*PI/nlength) = cos(-2*PI/nlength) + j*sin(-2*PI/nlength)
complex *pw = (complex *)malloc(nLength *sizeof(complex)/2);
double angle = 0.0;
for (int i = 0 ; i <nLength/2 ;++i)
{
angle =CV_PI *sign *2.0 * i /nLength ;
pw[i] = complex(cos(angle),sin(angle));
}
//位变换
int p = 0 ;
for (int i = 0 ; i <nLength ;++i)
{
p = 0 ;
for (int j = 0 ; j <nlevel ; ++j)
{
if (i & (1<< j) )
p+=1<<(nlevel - j -1);
}
pFd[p] = pTd[i];
}
//蝶形算法
int B=0; //跨度间隔
int weight = 0 ; //加权系数
complex *x1 = (complex *)malloc(nLength * sizeof(complex));
for (int i = 0 ; i <nlevel ; ++i)
{
B = 1<<i; //跨度间隔 1 ,2 ,4 ,8 ..............
for (int j =0 ; j <B; ++j)
{
weight = (1<<(nlevel - i -1)) * j;
for (int k = j ; k <nLength ; k+=(1<<(i+1)))
{
x1[k] = pFd[k] + pFd[k+B] * pw[weight];
x1[k+B] = pFd[k] - pFd[k+B]*pw[weight];
}
}
memcpy(pFd,x1,nLength * sizeof(complex));
}
if (sign == 1)
{
for (int i = 0 ; i < nLength ; ++i)
pFd[i]/=nLength;
}
free(pw);
free(x1);
}