凸优化,优化问题的一个分支。凸优化模型对一般非线性优化模型进行局部逼近,依次为,求解无约束凸优化模型、等式约束凸优化模型以及包含不等式约束的凸优化模型。最小二乘和线性规划都属于凸优化问题。在组合优化以及全局优化方面,凸优化用来估计最优值的界以及近似解。难点是很多问题是非凸的。最好是发现问题是凸优化问题以及可以将其描述成凸优化问题。顺序是线性代数、线性规划、凸优化理论。数学优化问题:
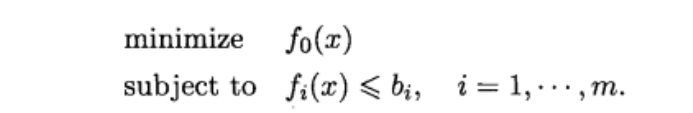
有优化变量、约束函数、目标函数、约束上下限(约束边界)。一般考虑具有特殊形式的目标函数和约束函数的优化问题。线性规划是其中一类,即目标函数和约束函数都是线性的。称为线性规划。
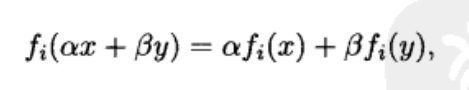
当优化函数不是线性的称为非线性规划。
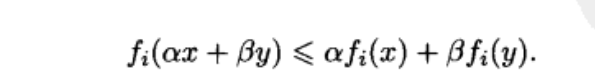
凸优化问题的目标函数和约束函数都是凸函数即:可以看出凸性是较线性更为一般的性质,故线性规划问题也是凸优化问题。
偏差最小,统计学意义上的更加相似。若某个问题中的每个约束函数仅仅取决于为数不多的几个变量,称此问题是稀疏的。最小二乘与线性规划是应用最广泛的两类凸优化问题。最小二乘是无约束条件的优化问题也是可微的:
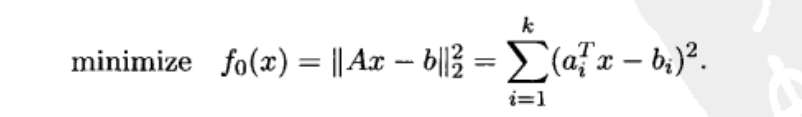
其解可化为一般的一组线性方程组进而求得解析解:ATAx=ATb。最小二乘法是回归分析、最优控制以及很多参数估计和数据拟合方法的基础。判断一个优化问题是否是最小二乘问题很简单,只需检验目标函数是否是二次函数,再检验二次函数是否是半正定,最小二乘问题有一个简单固定的表达式。在加权最小二乘问题中:
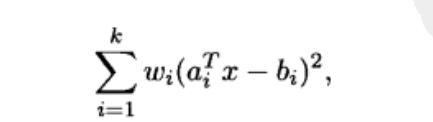
正则化是解决最小二乘问题的另一个技术。一个最简单的形式是在成本函数中增加一项和变量平方和成正比的项:
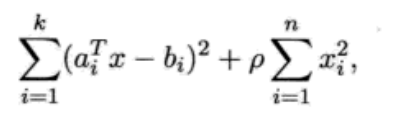
rou大于0,此问题亦可以转化为标准最小二乘问题,当x的值较大时,增加的项对其施加一个惩罚,使其得到的解比仅优化第一项时更加切合实际。在统计估计中,x的分布已知,可采用正则化方法。
线性规划其目标函数和所有的约束函数均为线性函数,线性规划问题可以有如下表达,
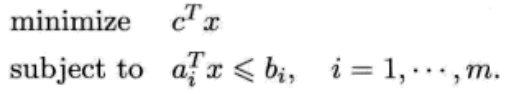
虽然线性规划问题的解并没有一个简单的解析表达形式(和最小二乘问题不同)
凸优化问题的解并没有一个解析表达式,内点法较为有效,内点法可以在多项式时间内给定精度求解这些优化问题,内点法可以在10到100步之间解决凸优化问题。对于凸优化问题的几类重要问题,如二阶锥规划和几何规划问题,内点法越来越成熟。