最短路

参考：http://blog.csdn.net/shuangde800/article/details/7987100

Foyed算法(动态规划):

i,j之间的最短路要么直接相连，要么通过一系列其他的点。

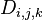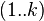设 $D_{i,j,k}$ 为从 $i$ 到 $j$ 的只以 $(1..k)$ 集合中的节点为中间节点的最短路径的长度。 //状态的定义十分重要,要想清楚,不然搞死你.

那么d[k][i][j]=min(d[k][i][j],d[k-1][i][k]+d[k-1][k][j]);枚举k，(1,2,3,4,5,6,,,,,,n),对于任意的i，j来说，要么选k，要么不选k。

不选k，问题转化成d[k-1][i][j]，选k，问题转化成求d[k-1][i][k]+d[k-1][k][j]

观察递推式，

for(int k=1;k<=N;k++)

for(int i=1;i<=N;i++)

for(int j=1;j<+N;j++)

d[i][j]=min(d[i][j],d[i][k]+d[k][j]);

Dijkstra算法(贪心)

贪心策略：每次在未找出最短路的点中选取距离源点最近的点，对此点进行标记表明已经是最短路径，然后更新与其相连的点,；重复此操作，直到更新完毕。

有两种方式选取距离源点最近的点：

1 int m=inf=10e18;

for(int y=0;y<n;y++) if(!v[y] && d[y]<=m) m=d[x=y];

2 利用优先队列，从源点开始每次将被更新的点加入优先队列。然后就可以选出d值最小的了。

如果对Dijkstra算法核心思想不是很理解，可能会问：Dijkstra算法为什么不能处理负权边？

Dijkstra由于是贪心的，每次都找一个距源点最近的点（dmin），然后将该距离定为这个点到源点的最短路径（d[i] ← dmin）；但如果存在负权边，那就有可能先通过并不是距源点最近的一个次优点（dmin’），再通过这个负权边 L (L < 0)，使得路径之和更小（dmin’ + L < dmin），则 dmin’ + L 成为最短路径，并不是dmin，这样Dijkstra就被囧掉了。比如n = 3，邻接矩阵：

0， 3， 4

3， 0，-2

4，-2， 0

用Dijkstra求得 d[1，2] = 3，事实上 d[1，2] = 2，就是通过了 1-3-2 使得路径减小。Dijkstra的贪心是建立在边都是正边的基础上，这样，每次往前推进，路径长度都是变大的，如果出现负边，那么先前找到的最短路就不是真正的最短路，比如上边的例子，这个算法也就算废了。

另外，Dijkstra算法时间复杂度为O(V² + E)。源点可达的话，O(V * lgV + E * lgV) => O(E * lgV)。当是稀疏图的情况时，此时 E = V²/ lgV，所以算法的时间复杂度可为 O（V²）。若是斐波那契堆作优先队列的话，算法时间复杂度为O（V * lgV + E）。

Bellman_floyed算法(对每条边进行n-1次松弛操作，因为最短路最多经过n-1个节点)

Bellon-Ford算法，每次都松弛所有的边，所以造成效率低下，而SPFA的高效之处在于，它每次只松弛更新过的点连接的边，

从初始状态,得到所有状态的值，

可以有两种考虑方式：

1：每个状态都被能到达它的状态更新过。

2：每个状态更新它能到达的所有状态(每次通过当前状态更新它能到达的所有状态)

结果都是所有状态都被更新过。

其实就是Bellman_foyd(1)和Spfa(顺推(2:从初始状态一直更新完))算法的区别.

简单的过程叙述就是：

1）初始 Dis[s] = 0，其他赋值为Inf；
2）将起点s放入空队列 Q；
3）step 1. 从 Q 中选取元素u，并删除该元素；
4）step 2. 对所有和 u 相连的点 v 进行松弛，如果 v 被更新且 v 不在队列中，把 v 加进队列；
5）一直循环 step 1 和 step 2，直到队列为空。结束；

HH师兄，当年讲SPFA算法时，提到过三个问题，不妨思考一下，可以帮助更好的理解SPFA算法：

n1. 想想怎么判断负环的情况？
n2. 为什么要判断v是否在队列？
n3. 怎么样有效的判断v在不在队列之中？

答案如下：

1）如果一个节点更新了 n 次，那么存在负环；
2）如果有多个 v 在队列,第一个 v 已经把松弛做完了，剩下的 v 属于无效操作；
3）用一个数组Inqueue[]，在元素进队的时候表示成 True，出队的时候标记成 False，判断的时候只要看看Inqueue[v] 是否为 True 就行了；

另外，还需要了解的是，SPFA 的算法时间效率是不稳定的，即它对于不同的图所需要的时间有很大的差别。在最好情形下，每一个节点都只入队一次，则算法实际上变为广度优先遍历，其时间复杂度仅为O(E)。另一方面，存在这样的例子，使得每一个节点都被入队(V – 1)次，此时算法退化为 Bellman-ford算法，其时间复杂度为O(VE)。

SPFA在负边权图上可以完全取代 Bellman-ford 算法，另外在稀疏图中也表现良好。但是在非负边权图中，为了避免最坏情况的出现，通常使用效率更加稳定的 Dijkstra 算法，以及它的使用堆优化的版本。通常的SPFA算法在一类网格图中的表现不尽如人意。

SPFA算法（用队列对Bellman_floye算法进行优化）

采用类似于宽搜的方式，对每条边进行松弛操作。

在最好情形下，每一个节点都只入队一次，则算法实际上变为广度优先遍历，其时间复杂度仅为O(E)。另一方
面，存在这样的例子，使得每一个节点都被入队(V-1)次，此时算法退化为Bellman-ford算法，其时间复杂度为
O(VE)。

两大最强最短路算法，SPFA和Dijkstra算法的比较：

SPFA：执行松弛操作，用队列里有的点去刷新起始点到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后，判断负环的话，需要记录一个节点的入队次数，超过|V|则存在负环。用SPFA的时侯，同一个节点可能会多次入队，然后多次去刷新其他节点，这样就会导致最短路条数出现重复计算（所以才能判断负环)，而Dijkstra使用优先队列，虽然同一个点可以多次入队，但是mark数组保证了一个点真正pop出来刷新其他点的时候只有一次，而且必定满足最短路！

SPFA 和 Dijkstra 同一个节点都有可能入队多次，但是，由于Dijkstra算法不考虑负环的情况，使用优先队列，则每次pop()出来的都是最小的权值的点去刷新其他的点，因此可以保证满足最短路，同时用mark数组控制可以保证每个节点出来刷新其他节点的机会只有一次，因而保证了计算最短路径的次数不会出现重复。

而SPFA考虑到负环的情况，每个节点可以多次刷新其他节点，以此才能得到最短路并且判断是否存在负环，使用时只需要确保相同节点不要同时出现在队列中即可，由于每个节点可以多次刷新其他节点，因此，计算最短路径数时会有重复。

也就是，如果有负权边，则使用SPFA；如果都是正权边，Dijkstra + 优先队列效率更高，且更靠谱些。

从时间复杂度来分析算法，

Spfa 算法节点(状态)里面存的是编号。

从每个节点进队的次数来分析，也就是DP中被更新的次数，在最短路中就是有多少条路到达这个节点。时间复杂度就为每个节点被更新的次数，在最短路中就是节点的进队次数，从DP的角度来分析的话，被更新了就要再去更新别人

最好情况下 o(m)

变成bfs，每个节点只进队一次，时间复杂度为o(m)

最坏情况下o(n*m)

变成bellman_foyd算法，

从点的角度来考虑：

A：每个节点进队n-1次，（假设到达此节点的路的长度为k，长度为k的路的节点只进队一次，虽然可能会有多条，但是从bfs树的角度来考虑，长度为k的路确实只有一条是最短路，所以只进队一次，而k的范围为1到n-1，所以每个节点进队的次数最多为n-1次），

B：从bfs树来考虑，最多有n-1层，每个节点在每一层都有可能被更新，但是对于每一层来说，每个节点被放进队列的机会最多只有一次，因为层数确定，长度确定的路径只有一条最短路径。

每个节点都进队一次的时间复杂度为o(m),那么进队n-1次的时间复杂度就为o(n*m).

Dijkstra m*log(n) 节点(状态)里面存的是编号和权值

每次都是已经求出最短路的点去更新，从这个角度去考虑，所以总共有n个点

从优先队列弹出 log(n)的复杂度，每个已经求出最短的点去更新别的点，

并且每个点只有一次更新其他状态的机会，n个点总共更新m次，时间复杂度为m*log(n).

spfa与Dijkstra的区别

spfa中一个节点可以多次被更新，也可以多次去更新别人

Dijkstra中一个节点可以多次被更新，但是只能更新别人一次。每次都是选当前最短路的那个点去更新别人，因为它有可能被到达，但是不可能被更新。

标记的使用，队列里可能会有多个相同的节点，但是只让优先队列里弹出来的那个去更新别人