原题链接 https://www.luogu.com.cn/problem/P2679
题目大意
给你两个字符串 $A$ 和 $B$,问你有几种方案使得将 $B$ 分成不重复 $k$ 段后每段在 $A$ 中依次出现;
题解
一般这种字符串 $dp$,还是两个字符串瞎搞的这种,状态设置是有套路的,然而我就不知道;
例如我们要求两个序列的 $LCS$,我们可以这样设置状态:
$dp [ i ][ j ]$:第一个序列的 $1$~$i$ 和第二个序列的 $1$~$j$ 的 $LCS$ 是多少;
转移的话我们只需从前往后扫,按照每次添加一个字符的方式进行转移;
这个题也可以这么设置状态,只是多了一个维度而已,正所谓 $zhx$ 说过:多一个限制就多一个维度!
状态设置
$dp [ i ][ j ][ k ]$:将 $B$ 串的 $1$~$j$ 分成不重复的 $k$ 段,使得这 $k$ 段在 $A$ 中的 $1$~$i$ 中依次出现的方案数是多少;
转移的话我们需要考虑分段的问题;
如果当前的 $A [ i ] == B [ j ]$,那么说这个字符可以与上一个字符连起来作为一个更长的段,也可以独自成一段;如果 $A [ i ] != B [ j ]$,那么就不能匹配,需要继续枚举下去;
但是当前状态并不能解决是否与前面连成一段的问题;
我们再在此基础上加一个维度:
$dp [ i ][ j ][ k ][ 0/1 ]$: 将 $B$ 串的 $1$~$j$ 分成不重复的 $k$ 段,使得这 $k$ 段在 $A$ 中的 $1$~$i$ 中依次出现,第 $i$ 个字符选不选的方案数是多少;
什么意思呢?举个例子说一下啦:
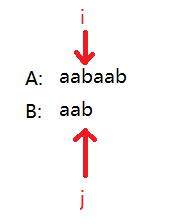
我们发现 $A [ i ] == B [ j ]$,根据上面的说法,我们现在有两种抉择:
1. 让这个 $b$ 和前面的 $a$ 共为一段;
2. 让这个 $b$ 单独成一段;
状态转移
分为两种情况来讨论:
①:$A [ i ] == B [ j ]$:
那么我们现在有三种抉择了:
<1> 让当前字符与前面的字符连成一段,前提条件就是我们要都选上 $A [ i ]$ 和 $A [ i-1 ]$:
$dp [ i ][ j ][ k ][ 1 ] += dp [ i-1 ][ j-1 ][ k ][ 1 ]$;
<2> 让当前字符独自成段,前提条件就是我们要选上 $A [ i ]$,但 $A [ i-1 ]$ 的情况无所谓:
$dp [ i ][ j ][ k ][ 1 ] += dp [ i-1 ][ j-1 ][ k-1 ][ 0 ] + dp [ i-1 ][ j-1 ][ k-1 ][ 1 ]$;
<3> 我们不选当前的 $A [ i ]$,但 $A [ i-1 ]$ 的情况无所谓:
$dp [ i ][ j ][ k ][ 0 ] += dp [ i-1 ][ j ][ k ][ 1 ] + dp [ i-1 ][ j ][ k ][ 0 ]$;
②:$A [ i ] != B [ j ]$:
<1> 毫无疑问,我们被迫不选 $A [ i ]$,但 $A [ i-1 ]$ 的情况无所谓:
$dp [ i ][ j ][ k ][ 0 ] += dp [ i-1 ][ j ][ k ][ 0 ] + dp [ i-1 ][ j ][ k ][ 1 ]$;
<2> 哼,我偏要选!$Sorry$啦,方案数为 $0$ $qwq$:
$dp [ i ][ j ][ k ][ 1 ] = 0$;
发现舍弃 $A [ i ]$ 时的转移方程是一样的,所以我们可以合到一块去,那么代码是长这个亚子滴:
for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { for(int k=1;k<=K;k++) { dp[i][j][k][0]+=(dp[i-1][j][k][0]+dp[i-1][j][k][1])%mod; //不选A[i]时代码一样 if(A[i]==B[j]) //若相等,可以与前面的连成一段,也可以独自成段 dp[i][j][k][1]+=((dp[i-1][j-1][k][1]+dp[i-1][j-1][k-1][0])%mod+dp[i-1][j-1][k-1][1])%mod; else dp[i][j][k][1]=0; //不相等偏要选?方案数为0 } } }
边界设置
也就是刚开始 $B$ 什么都没有的情况,那么对于任意的 $i(i∈n)$,都有 $dp [ i ][ 0 ][ 0 ][ 0 ] =1$;
for(int i=0;i<=n;i++) dp[i][0][0][0]=1;
但是会 $MLE$,$O(nm^2)$ 直接 $boom$!
考虑到每次转移只与 $A$ 串的前一个字符有关,所以我们可以滚动数组,只需开两个空间就够了,分别存当前状态和上一个状态;
转移的时候不能写 $+=$ 了,而是要直接赋值,不然你懂得$qwq$;
还需要用到位运算的小技巧,我们可以用 ^ 来实现 $0$~$1$ 的转化,也就是说如果 $i$ 是当前状态,$i$^$1$ 就是上一个状态;
$Code$:
#include<iostream> #include<cstdio> #include<cmath> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } const int mod=1e9+7; const int N=1005; char A[N],B[N]; int n,m,K; long long dp[2][205][205][2]; int main() { n=read();m=read();K=read(); scanf("%s",A+1);scanf("%s",B+1); dp[0][0][0][0]=dp[1][0][0][0]=1; //边界只需更新这两个就好了 for(int l=1;l<=n;l++) { int i=l%2; //当前状态 for(int j=1;j<=m;j++) { for(int k=1;k<=K;k++) { dp[i][j][k][0]=(dp[i^1][j][k][0]+dp[i^1][j][k][1])%mod; //不选A[i]时代码一样 if(A[l]==B[j]) //注意这里不是A[i]!!! dp[i][j][k][1]=((dp[i^1][j-1][k][1]+dp[i^1][j-1][k-1][0])%mod+dp[i^1][j-1][k-1][1])%mod;//若相等,可以与前面的连成一段,也可以独自成段 else dp[i][j][k][1]=0; //不相等偏要选?方案数为0 } } } printf("%lld ",(dp[n%2][m][K][0]+dp[n%2][m][K][1])%mod); //这里也别忘了改 return 0; }