今天是黄致焕老师的讲授~
T1



自信 AC 莫名 80 pts???我还是太菜了!!
对于每种颜色求出该颜色的四个边界,之后枚举边界构成的矩阵中每个元素,如果不等于该颜色就标记那种颜色不能最先使用。
注意特判整张图只有一种颜色的情况。(这个坑点坑掉我 10 pts!)
枚举时注意跳过所有已经被删除的元素。(不然 #8 死活过不去)
T2




T3




基础算法
模拟
模拟是算法竞赛中最简单,也是最难的一类题;
简单的地方在于只需要读清楚题目的所有要求并一步步实现就行了;
难点同样必须读清楚题目的所有条件并一步步实现;
在早年的联赛中比较常见,在今年联赛中出现的频率有所降低;
一般这类题型需要大脚大量的耐心以及码力,建议优先功课其他题目;
P3952 时间复杂度
小明正在学习一种新的编程语言 A++,刚学会循环语句的他激动地写了好多程序并给出了他自己算出的时间复杂度。下面请你编写程序来判断小明对他的每个程序给 出的时间复杂度是否正确。
A++语言的循环结构如下:
F i x y
循环体
E
其中 F i x y 表示新建变量 i(变量 i 不可与未被销毁的变量重名)并初始化为 x,然后判断 i 和 y 的大小关系,若 i 小于等于 y 则进入循环,否则不进入。每次循环结束后 i 都会被修改成 i+1 ,一旦 i大于 y 终止循环。 x 和 y 可以是正整数(x 和 y 的大小关系不定)或变量 n 。n 是一个表示数据规模的变量,在时间复杂度计算中需保留该变量而不能将其视为常数,该数远大于 100。 “ E ” 表示循环体结束。循环体结束时,这个循环体新建的变量也被销毁。
题解:
首先判断是否存在语法错误;
之后对于每个循环,判断复杂度为 O ( n ) ,O ( 1 ),还是根本不会进去。
将程序抽象成一棵树,每个循环向外层循环根据复杂度连边,如果 O ( n ) 权值为 1,如果 O ( 1 ) 权值为0,如果不进去就不建立点。
最后找到深度最大的点即可。
P3585 [POI2015]PIE
一张 n * m 的方格纸,有些格子需要印成黑色,剩下的格 子需要保留白色。
你有一个 a * b 的印章,有些格子是凸起(会沾上墨水) 的。
你需要判断能否用这个印章印出纸上的图案。 印的过程中需要满足以下要求:
1 印章不可以旋转。
2 不能把墨水印到纸外面。
3 纸上的同一个格子不可以印多次。
数据范围 n , m , a , b ≤ 1000
题解:
首先需要将印章最外圈没有墨水的部分裁掉。
纸上最左上角的有墨水的点一定是印章上最左上角有墨水的点印的。
每次不断重复将印章的痕迹删除的操作即可,删除时注意只枚举印章上有墨水的点。
可以实时维护每行第一个有墨水的格子进行优化。 时间复杂度 O ( n * m );
P3492 [POI2009]TAB-Arrays
给出两个 n * m 的矩阵,保证每个矩阵内元素互不相同且 权值均在 [ −106 , 106 ] 之间,请能否把其中一个矩阵通过若干次交换两行或者交换两列的操作变成另外一个矩阵;
数据范围 n , m ≤ 1000
题解:
注意到无论如何变换,本来在同一行的元素依然在同一 行,本来在同一列的元素依然在同一列。
所以我们可以将两个矩阵中的行和列一一对应起来,之后再检查是否所有元素都符合条件即可。
时间复杂度 O ( n * m );
贪心
贪心的核心思想是通过一步步的局部最优获得全局最优。
判断依据某种“短视的”贪心选择性质,性质的好坏决 定了算法的成败。
找到这种性质便是贪心算法最重要的一步。
贪心算法代码实现简单,且时空复杂度较低 。
P3419 [POI2005]SAM-Toy Cars
Jasio 是一个三岁的小男孩,他最喜欢玩玩具了,他有 n 个不同的玩具,它们都被放在了很高的架子上所以 Jasio 拿不到它们 。为了让他的房间有足够的空间,在任何时刻地板上都不会有超过 k 个玩具 。 Jasio 在地板上玩玩具。 Jasio 的妈妈则在房间里陪他的儿子。 当 Jasio 想玩地板上的其他玩具时,他会自己去拿,如果他想玩的玩具在架子上,他的妈妈则会帮他去拿,当她拿玩具的时候,顺便也会将一个地板上的玩具放上架子使得地板上有足够的空间 。 他的妈妈很清楚自己的孩子所以他能够预料到 Jasi o想玩些什么玩具 。所以她想尽量的使自己去架子上拿玩具的次数尽量的少,应该怎么安排放玩具的顺序呢?
k, n ≤ 100000, p ≤ 5 * 105 .
题解:
容易想到妈妈每次一定会将最晚使用的玩具放回架子。
用一个堆维护即可。
时间复杂度 O ( p log k );
[CF898D]Alarm Clock
有 n 个闹钟,第 i ( 1 ≤ i ≤ n ) 个闹钟将在第 ai ( 1 ≤ ai ≤ 106 )分钟鸣响,鸣响时间为一分钟。当在 连续的 m 分钟内,有至少 k 个闹钟鸣响,则会被叫醒。现要求关闭一些闹钟,使得在任意连续的m 分钟内,鸣响的闹钟数量恒小于 k 。
题解:
将所有闹钟按照时间排序,之后从左向右扫。只要碰到会吵醒的情况,就把当前闹钟关闭。
每当出问题时,我们都选择最右面的关闭,这样能保证对后面的影响尽量少,会让剩余需要关的闹钟尽量少。 时间复杂度 O ( n log n );
P3545 [POI2012]HUR-Warehouse Store
一共有 n 天,第 i 天上午会进货 Ai 件商品,中午的时候会有顾客需要购买 Bi件商品,可以选择满足顾客的要求, 或是无视掉他。 如果要满足顾客的需求,就必须要有足够的库存。问最多能够满足多少个顾客的需求。
n ≤ 250000, Ai , Bi ≤ 109 .
题解:
容易想到能卖就卖的思路。
然而如果有一个需求很大的顾客买了,有可能导致后来很多需求较小的顾客买不到商品 。
考虑退货制度,如果当前顾客买不了商品,可以要求之前购买量最大,且购买量比当前顾客高的顾客进行退货,换成当前顾客。
用一个堆来维护之前所有购买了的顾客即可。
时间复杂度 O ( n log n );
[CF954E]Water Taps
给定 n 个水龙头,第 i 个水龙头有最大出水量 Ai,且给定 一个温度值 ti 。
定义一次出水得到的温度为 Σ ( Ai * ti ) Σ ( Ai ) ,给定一次出水得到的温度 T,求最大总出水量 。 如果得不到该温度,输出0 ;
1 ≤ n ≤ 2 * 105 , 0 ≤ Ai ,ti ≤ 106
题解:
先把 ti 减去 T ,然后按照 t 排序把数组分成两块,一半小于等于 0,一半大于 0 ;
用贪心的思想可以发现有一半必须全选,另一半选最靠近 T 的那些;
证明: 假设负数集里面还有一些没选,正数集里还有数剩余那么我们就可以把他们凑出一个 0 出来,直到某一边用完为止;
证毕。 所以就可以直接贪心了 。
P3457 [POI2007]POW-The Flood
你手头有一张该市的地图。这张地图是边长为 m * n 的矩形,被划分为 m * n 个 1 * 1 的小正方形。对于每个小正方形,地图上已经标注了它的海拔高度以及它是否是该市的 一个组成部分。地图上的所有部分都被水淹没了。并且,由于这张地图描绘的地面周围都被高山所环绕,洪水不可能自动向外排出。显然,我们没有必要抽干那些非该市的区域。 每个巨型抽水机可以被放在任何一个 1*1 正方形上。这些巨型抽水机将持续地抽水直到这个正方形区域里的水被彻底抽干为止。当然,由连通器原理,所有能向这个格子溢水的格子要么被抽干,要么水位被降低。每个格子能够 向相邻的格子溢水,“ 相邻的 ” 是指 ( 在同一高度水平面上的射影 ) 有公共边。
n, m ≤ 1000
题解:
首先将所有格子从小到大排序。
从小到大枚举每一种海拔,用并查集将所有海拔小于等于当前枚举值的格子并起来。
考虑每一个等于当前海拔的城市区域格子,如果该格子所在并查集中没有抽水机,就需要在该并查集中建立一 个抽水机,因为该城市不可能由外部区域的抽水机抽干。
时间复杂度 O ( n * m log ( n * m ) );
[NOIP2012]国王游戏
恰逢 H 国国庆,国王邀请 n 位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数, 国王自己也在左、右手上各写一个整数。然后,让这 n 位大臣排成一排,国王站在队伍的最前面。排好队后, 所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数,然后向下取整得到 的结果。 国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
N ≤ 100000.
题解:
首先对于一个交换题来说 i 和 i + 1 交换必不影响其他位置的贡献。
设 S 是前面的乘积,ai 是左手上的数,bi 是右手上的数 。那么不需要交换等价于 max ( S / bi , S * ai / bi + 1 ) < max ( S / bi + 1 , S * ai+1 / bi )。乘上 bi * bi + 1 / S,得到 max ( bi + 1 , ai * bi ) < max ( bi , ai+1 * bi + 1 ) 。
max ( bi + 1 , ai * bi ) < max ( bi , ai+1 * bi+1 ) 。由于 bi+1 必小于 ai+1 * bi+1 ,ai * bi 大于 bi ,要求上式成立,则有 ai * bi < ai+1 * bi+1 。交换还要求比较函数是一个全序,不能 A 比 B 好,B 比 C 好,C 比 A 好 。按照 ai * bi 排序即可 。
P3566 [POI2014]KLO-Bricks
给定每种颜色的砖块数量,相同颜色的砖块不能放在一 起,两头颜色已经确定,构造一种方案。
n ≤ 106
题解:
首先将两头的颜色减去。
考虑从左向右放砖块,每次优先放所有能放的颜色中数量最多的颜色。
当几种颜色数量相同时,优先放最右侧砖块的颜色。
时间复杂度 O ( n ) 。
二分
二分的思想
给定一个单调的函数/数组;
给定一个值,求这个值是否存在;
或者找到这个值应当存在的位置;
由于数组有序,不妨认为他单调递增;
假设 Ai > x,则必然有 ∀ j > i, Aj > x ;
假设 Ai < x,则必然有 ∀ j < i, Aj < x ;
二分的原理就是每次在待定区间中选择mid。
必然可以确定一边是没有意义的。
每次问题的规模缩小1/2 ;
因此复杂度为 O ( log N );
二分答案
顾名思义,就是对答案进行二分;
对于某些要求 “ 满足某条件的最小值 ” 类的问题,对答案进行二分,假设答案不超过 mid,则问题变为 “ 满足某条件且某值不超过 mid ” 的判定性问题。
常用于最大值最小化类问题。
在二分答案之后往往需要一个贪心策略。
P3523 [POI2011]DYN-Dynamite
给一棵树,树上有一些关键节点,要求你选 m 个点,使得关键节点到这些点中距离的最小值的最大值最小,求这个值。 数据范围:n , m ≤ 3 * 105 ;
题解:
二分答案。
二分答案后在树上进行递推。
用 f [ i ] 表示子树内距离根最远,并且还未找到最近点的关键点和子树根的距离。
用 g [ i ]表示子树内距离根最近的被选择点和子树根的距离;
时间复杂度 O ( n log n );
P3534 [POI2012]STU-Well
给定一个非负整数序列 A,每次操作可以选择一个数然后减掉 1,要求进行不超过 m 次操作使得存在一 个 Ak = 0 且 max ( | Ai − Ai−1 | ) 最小,输出这个最小值以及此时最小的 k;
数据范围:n ≤ 106 , m ≤ 1018
题解:
首先二分 max ( | xi − xi−1 | ) 的值为 t 。
从前向后,从后向前分别扫过所有数,将过大的数变小使得任意两个相邻的数差不超过 t 。
之后枚举 k,表示将 Ak 变为 0 。
同时维护 l , r,表示区 间 [ l , r ] 中的所有数都要修改。
时间复杂度 O ( n );
二分是对一个单调的函数进行的操作;
那么我们有没有办法对一个单峰的函数进行操作呢?
求一个单峰函数的极值点;
参考二分的做法,我们把区间划成三份。
然后比较中间两个点的大小来进行一下讨论;
三分
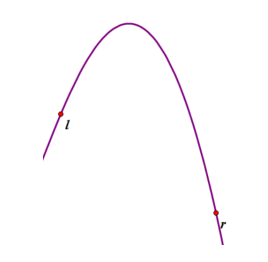
显然在 r 右侧的点都不会成为答案;

显然在 r 右侧的点都不会成为答案;
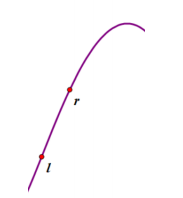
显然在 l 左侧的点都不会成为答案;
总结
发现共性:
l , r 中值较小的那一段一定会被舍去;
严格的实现每次都能缩小问题的 1/3;
事实上我们取两次 mid 会好写很多,只是常数问题;
例一
初始有一个为空的集合,要求支持两种操作:
1. 不断向集合中插入一个数,且这个数比集合中所有数都大;
2. 在集合中找一个子集,使得找到的子集 S 中的最大值减去子集 S 中元素的平均值的差最大,并输出这个差;
操作数 ≤ 500000
题解:
如何选取子集?
最后插入的这个数是一定要选的,然后再选小的数;
就是一个最大数加上几个用来拉低平均值的小数构成了所需子集;
小数一定是从最小值开始连续增加使平均值减小,直到达到一个临界点;
再增加小数就会使平均值增大,易知这是一个单峰函数;
因此考虑三分选多少小数即可;
分治的思想
将一个问题划分成若干个(一般都是分成俩)子问题;
分别解决每个子问题后(也可能是前,还可能一前一后之类的);
将各个子问题组合起来得到原问题的答案。
快速幂
如何快速计算 Xk?
我们将 k 进行二进制拆分。
比如我们需要计算 X11 ,即我们需要计算 X 2^0 + 2^1 + 2^3 ;
因此我们只需要计算 log k 次即可;
归并排序
基本思想:先将整个数组分成两个部分,分别将两个部分排好序,然后将两个排好序的数组 O ( n ) 合并成一个数组。
我们将问题分为两个阶段:分、治;
分
对于每个长度 > 1的区间,拆成两个 [ l , mid ] 区间和 [ mid + 1 , r ] 区间直接递归下去;
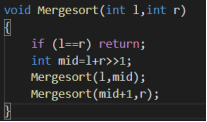
治
我们认为在处理区间 [ l , r ] 时,已经有 [ l , mid ] 和 [ mid+1 , r ] 内分别有序;
这一次的操作就是合并两个有序序列,成为一个新的长有序序列;
用两个指针分别指向左右分别走到哪了即可;
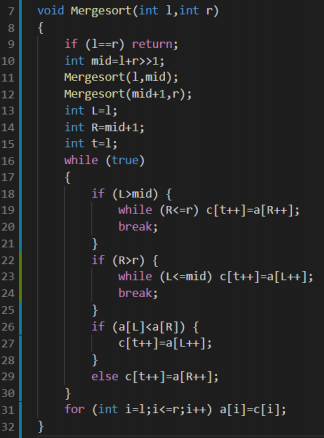
逆序对
给定一个 1 ∼ n 的排列,求逆序对数量。
1 ≤ n ≤ 105
逆序对:对于 1 ≤ x < y ≤ n, 若 A [ x ] > A [ y ],则称 ( x , y ) 为一个逆序对。
题解:
首先显然我们枚举 x , y 可以做到 O ( N2 );
分治: 假设当前问题 Work ( l , r ) 是求 l 到 r 区间内的逆序对数量。
讨论所有 ( x , y ) 可能在的位置: l ≤ x < y ≤ mid :子问题 Work ( l , mid ) x ≤ mid < y : ??? mid + 1 ≤ x < y ≤ r :子问题 Work ( mid+1 , r );
对于每个 mid 右边的数,我们要找到 mid 左边有多少比它大的数。
1) 对左侧排序,右侧在左侧上二分即可。
总时间复杂度 O ( n log 2n )
2) 归并排序: 对于数组 A 和数组 B 的归并过程,每当我们将 B 中的元素取出时:说明 A 中最小的元素比该元素大:说明 A 中所有元素比该元素大:说明答案 += A . size() ;
归并过程时间复杂度 O ( n ),总时间复杂度 O ( n log n )。
好了,我们已经学会了分治的概念,现在来练习一下吧!
[CF768B]Code For 1
有一个序列,初始时只有一个数 n 对于序列中每一个 > 1 的数,拆分成三个数 n/2 , n%2 , n/2 并替换原数。
直到序列中没有 > 1的数为止;
查询最终序列中 [ l , r ] 中有多少1;
0 ≤ n < 250 , 0 ≤ r − l ≤ 105
题解:
f [ n ] 为 n 展开后得到的数字个数:
f [ n ] = 2 * f [ n/2 ] + 1;
查询的时候判断一下是否在查询区间中即可;
TILE

题解:

手画 k = 0 的情况。
手画 k = 1 的情况。
考虑构造 k = 2。
k > 2 的情况就可以类似处理辣。
平面最近点对
给定二维平面上的 N 个点,求任意两点间的最近距离 (欧几里得距离)。
1 ≤ n ≤ 105
题解:
不妨按照 x 坐标排序。
对于区间 [ l , r ],我们将其分成 mid 左右两个部分。
两个点都在左侧:子问题 Work ( l , mid )
两个点都在右侧:子问题 Work ( mid+1 , r )
两个点一个在左侧,一个在右侧: 重点考虑第三种情况;
不妨假设左右两个子问题的答案为 ans 。则我们只需要考虑分界线两边距离不超过 ans 以内的点即可。
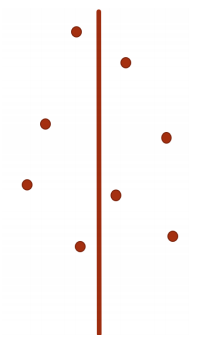
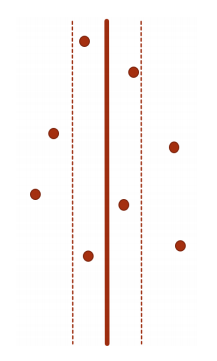
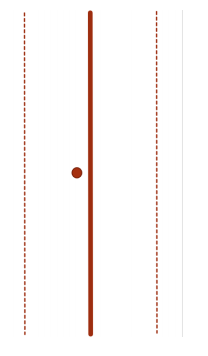
对于每个点,可能和它距离不超过 ans 的点坐标范围;
横坐标:[ mid - ans , mid + ans ];
纵坐标:[ y - ans , y + ans ];
每个小正方形内点数不可能超过一个(因为任意两点距 离不低于 ans)。故总点数不超过 6 个。除去该点自身, 该点至多需要和其他 6 个点求距离。
故该部分复杂度不超过 O ( n ) 。实现时可以直接对所有点按照 y 坐标排序,O ( n log2 n ),或者使用归并排序的技 巧,直接 O ( n log n ) 即可。
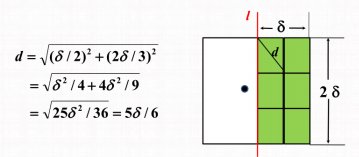
分治进阶
除了这些基本的分治方法之外,还有两种分治之后的常用 方法:
1. 合并法:
考虑我们要计算 Q 个区间的答案。
然后我们考虑分治,当分治中点在区间当中时,我们将这个区间在这一层处理。
一般的处理方法是从中点开始向左向右处理出一 些东西,然后合并即可。
2. 预处理法:
大约是 i 需要从1.. i−1的信息得到。
然后我们每次分治,然后每次计算 [ l , mid ] 对 [ mid + 1, r ] 的贡献。
二维LIS
给定数组 A , B,求最长的子序列,满足 ∀ i < j, Ai < Bi , Aj < Bj 。
N ≤ 100000。
题解:
既然一维 LIS 可以用树状数组做,那么二维 LIS 肯定可以树套树辣;
考虑更简单的写法,设 fi 表示到 i 为止的最长上升子序列;
则 fi = max (fj + 1)(j < i,Aj < Ai ,Bj < Bi)
那么我们考虑分治,分治到 [ l , r ] 时,由于 [ mid + 1 , r ] 不影响[ l , mid ] 的答案,首先递归 [ l , mid ] ,计算出 [ l , mid ] 中的所有 f ,然后考虑计算 [ l , mid ] 对 [ mid + 1 , r ] 的贡献;
根据要求,我们首先将左侧和右侧分别按 Ai 排序,然后右侧从小往大依次枚举,左侧维护一个树状数组,随着右侧 Ai 的增大依次往里面加入值;
注意到这样分治可以保证 [ 1 , i − 1 ] 里的每个决策至少和 i 分开了一次,所以肯定都会被算到,同时这样做的复杂度依旧是 O ( N log2 N )。
排列
给定一个排列 P,求:
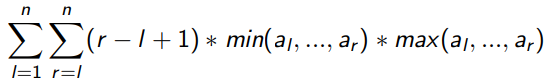
1 ≤ N ≤ 1000000。
题解:
如果说 min, max 只有一个出现的话,我们一般的常用方法是对最大 / 小值做分治构建笛卡尔树;
但是现在 min, max 都有,我们只能考虑之前提到的分治法:
对 [ 1 , n ] 开始分治,设当前分治到 [ l , r ] ;
我们处理所有 l ≤ mid ≤ r 的区间产生的贡献;
考虑从 mid 开始,向左向右预处理出到中心的最大最小值 Mini , Maxi 。
我们先简单的拆分一下式子:
( r − l + 1) * Min * Max = ( r + 1 ) * Min * Max − l * Min * Max
显然需要对 Min, Max 的情况进行分类讨论:
此时我们枚举右端点 r ,根据 Min, Max 的单调性,左端点将会分成连续的三段;
1. Minl > Minr , Maxl < Maxr ;
对于这种情况我们知道答案就是一段公差为1 的等差数列的和乘上一个固定的值;
2. 上述等式恰好有一个不满足。
不妨假设是 Maxl > Maxr , Minl > Minr ;
此时我们知道它仍然是连续的一段,同时我们需要维护 Maxl , Maxl * l 的前缀和,然后询问区间和即可;
3. 两个等式都不满足 Minl < Minr , Maxl > Maxr , 类似的,维护 l * Minl * Maxl 和 Minl * Maxl 的前缀和即可;
时间复杂度 O ( N log N )。
那么怎么维护这三段呢?
一个显然的方法是二分;
那么事实上,由于 r 在往右走的过程中,Min, Max 是在不断扩大的,所以第一段和第二段的左端点都在不断向左扩展;
我们只需要顺便维护这个过程即可。