求二分图的最大匹配数的算法
二分图:在一个图中,如果可以把这个图中的点集分成两部分,而边集中的每条边连接的两个顶点必须分别是这两部分点集中的一个点。
如
匹配:给定一个二分图G,在G的一个子图M中,M的边集{E}中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
如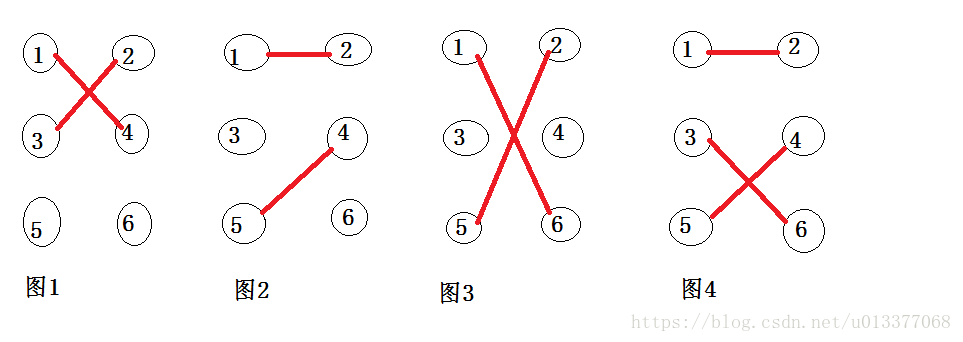
1求最大匹配,就是让相连的边能最多
2求最小点覆盖:求最少的点的个数,能连到所有的边等于最大匹配
证明:
假如已知最大匹配M,由最大匹配的定义可知,二分图K中的两个集合A,B中已经取出了最多个匹配点,即取出了最多个不共用一个点的路径。如果K中除了M中的点以外再没有其他任何点,那么显然K中所有路径已经被覆盖。如果K中除了M中的点还有其他点时,我们把这些点组成的集合定为L。对于任意x,y∈L,如果x∈A,y∈B,x,y间不可能存在路径,因为x,y∉M,x,y不能匹配。所以任意x∈L,如果x与其它点z连通,则z一定属于M。所以路径x--z也已经被z覆盖。由此可见,M中的点覆盖了所有存在的边,即最小点覆盖=最大匹配。
3:最小路径覆盖:选择最少的不相交的简单路径,覆盖所有的点。等于节点数-最大匹配数
证明:根据定义最小路径覆盖里要求同一个点只可以属于一条路径,即路径时不可以开叉的,如果在二分图里选两条有公共点的边那么反应在原图上就是路径有岔路,那么就不符合匹配的定义了,所以二分图里选的边必须是无公共交点的,这转化到最大匹配了。
4:最大独立集:选最多的点没有边相连:等于节点数-最大匹配
证明:。。。
模板
int pre[N];//当前的搭档
int line[N][N];//是否可连
int visit[N];//是否找过
bool find(int x)
{
rep(i,1,n+1)//n是边的数量
{
if(visit[i]==0&&line[x][i])//没被赵国且可以连接
{
visit[i]=1;//找过标记
if((pre[i]==0||find(pre[i]))&&pre[i]!=x)//当前没有匹配或能给他匹配的人再找一个匹配
{
pre[i]=x;
return true;
}
}
}
return false;
}
int main()
{
mm(line,0);
mm(pre,0);
int p;
sf("%d",&p);
while(p--)
{
sf("%d",&y);
line[x+1][y+1]=1;
}
int ans=0;
rep(i,1,n+1)
{
mm(visit,0);
if(find(i)) ans++;
}
}
int ans=0;
rep(i,1,n+1)
{
mm(visit,0);
if(find(i)) ans++;
}