复指数信号
现实生活中的信号一般可以看作是一个正弦波$f(t)=sin(omega t)$
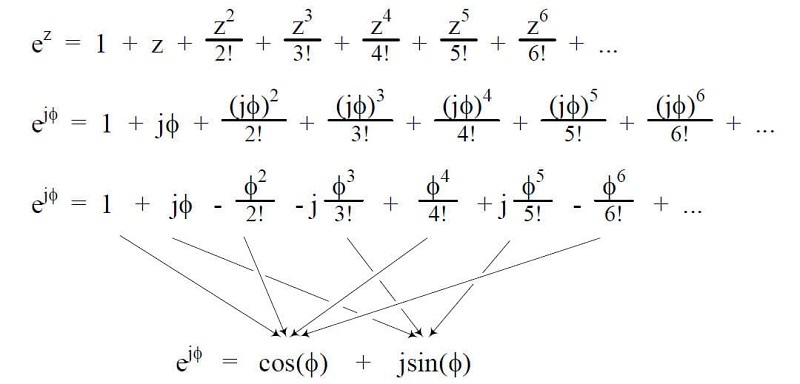
复指数信号是把信号在复数域进行表示,将三角函数转换为指数形式(利用欧拉公式)
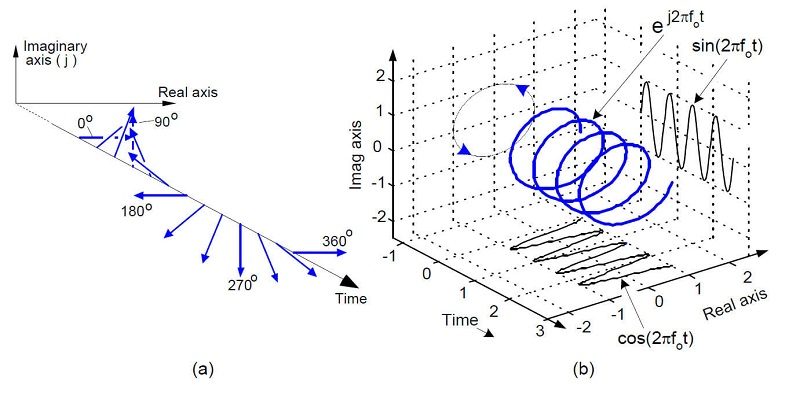
复信号可以看作是一个在空间随时间螺旋上升的信号,但实信号只表达了他的幅值大小。
用复信号表示实信号的公式:$cos(2pi f_0t)=frac{e^{j2pi f_0t}+e^{-2pi f_0t}}{2}$
实信号包含于复信号,可以用复信号来表示。现实生活中我们处理的都是实信号,傅里叶变换中之所以选用了复信号,而不是实的正弦信号,是因为用复信号的表示形式处理起来更简单。
连续域复指数信号具有以下性质:
- 周期性:$e^{jomega t}=e^{jomega(t+kfrac{2pi}{omega})}$
- $omega$越大,信号频率越快
- 对任意$|omega_1| eq|omega_2|$,信号$e^{jomega_1t},e^{jomega_2t}$相互正交
离散域复指数信号具有一下性质:
- 仅在$Omega/2pi$为有理数时,表现周期性
- 但当$Omega$为自变量时,有周期性
傅里叶变换
傅里叶变换是用来表示连续时间域中的非周期信号的。
$x(omega)=int_{-infty}^{+infty}X(omega)e^{jomega t}domega$,$X(omega)$为基信号的加权系数
在欧几里得空间中,一个向量可以表示为基向量之和。
同样,在信号空间中,向量也可以表示为基向量之和,也就是傅里叶变换的形式。
由于连续域复指数信号当$omega$不同时,就会有不同的基信号,基信号的数量是无穷的。因此需要采用积分来表示
可以用傅里叶变换进行表示的信号需要满足迪利克雷条件:
-
在任一有限区间内,连续或只有有限个第一类间断点;
-
在任一有限区间内,极大值和极小值的数目应是有限个;
- 在任一有限区间内,信号是绝对可积的。(说明信号能量是有限的)
傅里叶级数
傅里叶级数用于表示周期性的信号。
连续:$x(t)=x(t+kT_0)$
其基信号为$e^{jkomega_0t},(k=0, pm1,pm2,...)(omega_0=2pi/T_0)$
对应的傅里叶级数为$a_k=frac{1}{T}int_{T_0}x(t)e^{-jkomega_0t}dt$
相应的迪利克雷条件中任一有限区间内改为任一周期内
离散:$x[n]=x[n+N]$
为满足离散域中的周期性,$omega/2pi$需为有理数。因此基向量可取N个取值,即$e^{jkfrac{2pi}{N}n}$,$k$为任意$N$个连续整数
对应的傅里叶级数为$a_k=frac{1}{N}sum_{n=<N>}x[n]e^{-jkfrac{2pi}{N}n}$
基信号总结
| 周期性 | 非周期性 | |
| 连续 | $e^{jkomega_0t}$ | $e^{jomega t}$ |
| 离散 | $e^{jkfrac{2pi}{N}n}$ | $e^{jOmega n}$ |
离散傅里叶变换DFT
现实中处理的一般为有限区间的非周期的离散信号$x[n]$,当$n>N_1$时$x[n]=0$
对这类信号首先构造一个周期为$N(N>N_1)$的信号$ ilde{x}[n]$,$ ilde{x}[n]=x[n](0leq nleq N)$
通过傅里叶变换,可以得到信号的频率成分,从而排除噪音(因为噪音频率的值一般不高)
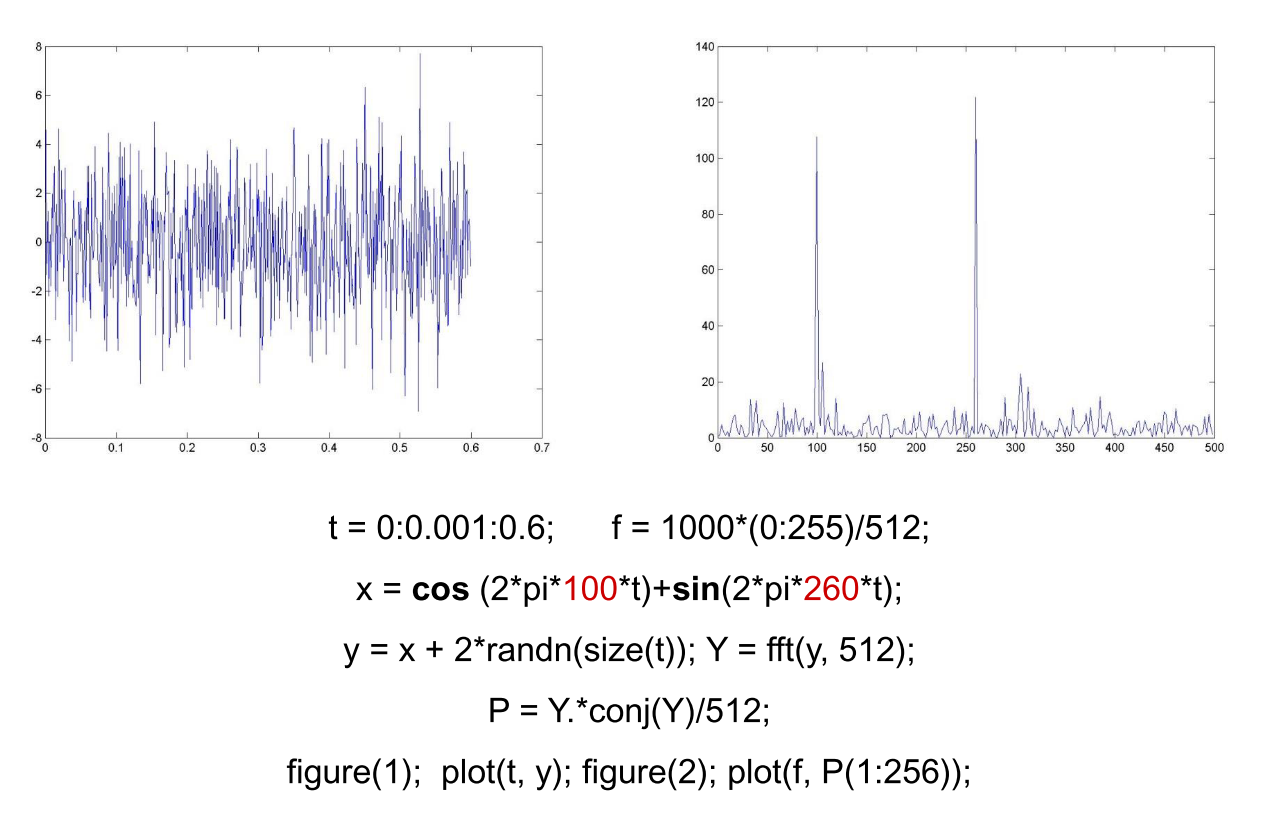
参考: