Catanlan Number
卡特兰数,又称卡塔兰数(Catanlan Number),是一个非常多见、高深的数列。它能解决我们数论题目中一些计数问题。前几项为:1,2,5,14,42,132,429,1430,4862,16796,58786……
那么如何求Catanlan Number的第N项呢?
1、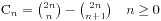
2、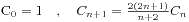
3、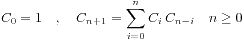
4、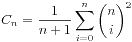
5、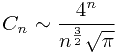
着重需要介绍一下的是卡特兰数的功能
例一:二叉树的计数
n个非叶节点的满二叉树的形态数(对称后得到的二叉树除非自己本身对称,否则算是不同),这里取Wikipedia上的一张图片说明问题:

问题分析:设该二叉树的左子树有i个节点,则右子树可想而知有n-i-1个节点。
我们可以使用f(n)来表示n个节点二叉树不同的形态数。
那么总和的答案就是我们的式3了。
例二:AB排列问题
有n个A和n个B排成一排,要求从序列的第一个开始无论到任何位置,B的个数不能超过A的个数。
问题分析:可以尝试用↗来表示A,用↘来表示B,那么我们可以画一个图标,最终是一个等腰直角三角形,你会惊讶地发现画完以后任何时候A都≥B。
例三:乘法加括号
一个序列A1*A2*A3*……*An,可以加括号改变该序列的运算顺序,问:有多少种不同的运算顺序?
问题分析:n=1时,A0*A1,f(1)=1
n=2时,A0*A1*A2,A0*(A1*A2),f(2)=2
……
以此类推,会发现答案是卡特兰数列的第N项。
我们也可以像二叉树计数问题那样得到f(0)*f(n-1)+f(1)*f(n-2)+……+f(n-1)*f(0)
发现答案就是卡特兰数、
例四:欧拉多边形分割问题
我们可以用n-3条互不相交的对角线将n边形分成n-2个互相没有重叠的三角形,输出有多少种不同的分法。
如N=6时,如下所示
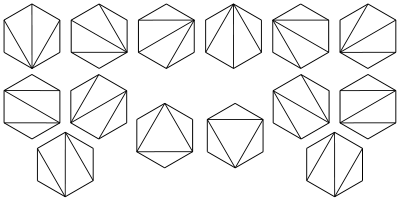
Catalan Number是一门非常高深的理论,如果有兴趣可以继续去研究。
[本文部分图片来自于:http://blog.csdn.net/duanruibupt/article/details/6869431]