1. 利用等概率Rand5生成等概率Rand3
这个题目可以扩展为:利用等概率RandM生成等概率RandN (M > N)
这里,我们首先明白一个简单的知识点:如果 randN 可以等概率生成 [0, N) 之间的数
假设 N = T的整倍数,那么我们可以直接使用 RandN() / (N / T) 来等概率生成 [0, T)之间的数
比如说,Rand21可以等概率生成[0, 21)之间的数,那么 Rand21() / 3 就可以等概率生成 [0, 7)之间的数,即 实现了 Rand7函数
// 利用 Rand5 实现 Rand3 int Rand3() { int tmp = Rand5(); while (tmp >= 3) { tmp = Rand5(); } return tmp; }
证明:以输出0为例,看看概率是多少。
x的第一个有效数值是通过Rand5得到的。Rand5返回0的概率是1/5,如果这事儿发生了,我们就得到了0,否则只有当Rand5返回3或4的时候,我们才有机会再次调用它来得到新的数据。
第二次调用Rand5之后,又是有1/5的概率得到0,2/5的概率得到3或4导致循环继续执行下去,如此反复。
因此概率的计算公式为:
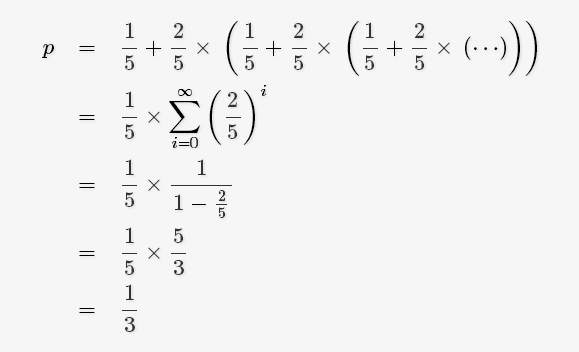
优化一下:我们在开始就说明了一个常识,这里,如果RandM 等概率 生成 RandN 时,当 M 很大 而 N 很小时,这时很多情况是在while里循环,可能一直循环
因此,我么把while循环的边界调整一下
int RandN() { int t = N; // t是小于M的,N的最大倍数 while (t + N < M) { t = t + N; } int tmp = RandM(); while (tmp >= t) { tmp = RandM(); } return tmp / (t / N); }
2. 利用等概率Rand3生成等概率Rand5
这个题目可以扩展为:利用等概率RandM生成等概率RandN (M < N)
这里,我们要首先 说明一个知识点:
我们可以利用 等概率RandM函数 生成 等概率 Rand(M * M)
比如说:M = 5
step1. Rand5 可以等概率生成 0, 1, 2, 3, 4 (1/5概率) step2. 设 上一步Rand5的结果为t,则 mul = M * t 等概率生成:0,5,10,15,20 (1/5概率) step3. 再次调用 Rand5 等概率生成 0, 1, 2, 3, 4 ,设结果为 s (1/5概率)
step4. 将step2 和 step3的两个结果相加, 就可以等概率生成 0,1,2...24 (相乘事件,1/25概率)
这样就实现了 Rand25
因为这一题中M < N, 而我们可以直接利用 RandM 来 等概率生成 Rand(M * M) ,这时 M * M 很可能就大于N了,如果不大于N,那么再次 翻倍即可
假设 M * M 大于 N,联想到第一题,相信大家很容易给出第二题的解了
int RandN() { int t = N; // t是小于M×M的,N的最大倍数 while (t + N < M * M) { t = t + N; } int tmp = RandM() * M + RandM(); // 等概率生成 Rand(M*M) while (tmp >= t) { tmp = RandM(); } return tmp; }
3. 单次遍历,等概率随机选取1个
(未知行数文件的一行文本/未知长度单链表的一个结点)
问题描述:假设我们有一堆数据(可能在一个单链表里,也可能在文件里),数量未知。
要求只遍历一次这些数据,随机选取其中的一个元素,任何一个元素被选到的概率相等。
O(n)时间,O(1)辅助空间(n是数据总数,但事先不知道)
解题思路:如果元素总数为n,那么每个元素被选到的概率应该是1/n。然而n只有在遍历结束的时候才能知道,在遍历的过程中,n的值还不知道,可以利用乘法规则来逐渐凑出这个概率值

void GetRandomSingleLine(FILE* fp, char* randomLine) { srand(time(NULL)); int i = 1; char tmp[MAX_LINE]; while (fgets(tmp, sizeof(tmp), fp) != NULL) { if (rand() % i == 0) { // rand() % i == 0 的概率为 1/i strcpy(randomLine, tmp); } ++i; } }
当文件行数为1时,rand() % 1肯定为0,直接输出
当文件行数为2时,rand() % 2 等于0 的概率为 1/2,此时 输出第一行 和 第二行 的概率均为 1/ 2
当文件行数为3时:
输出第一行的概率是:1 * (1 - 1/2) * (1 - 1/3) = 1/3
输出第二行的概率是:1 * (1/2) * (1 - 1/3) = 1/3
输出第三行的概率是:1 - (1/3 + 1/3) = 1/3 (注意:题目要求必须输出一行)

4. 单次遍历,等概率随机选取k个:蓄水池抽样问题
(未知行数文件的K行文本/未知长度单链表的K个结点)
解题思路:先读入第 1 ~ k 行保存,以后每次读入第 i 行,都以 k / i 的概率把刚读入的一行随机替换之前保存的 k 行中的一行。
void GetRandomLines(FILE* fp, char** randomLine, int k) { srand(time(NULL)); char tmp[MAX_LINE]; // 读入文件第1到k行 for (int i = 0; i < k; ++i) { fgets(randomLine[i], MAX_LINE, fp); } int i = k + 1; while (fgets(tmp, MAX_LINE, fp) != NULL) { if (rand() % i < k) { // 随机替换已有的某一行 int j = rand() % k; strcpy(randomLine[j], tmp); } ++i; } }

5. 等概率随机排列数组(随机洗牌 std::random_shuffle)
问题描述:假设有一个数组,包含n个元素。现在要重新排列这些元素,要求每个元素被放到任何一个位置的概率都相等(即1/n),
并且直接在数组上重排(in place),不要生成新的数组。用O(n) 时间、O(1)辅助空间。
解题思路:
先想想如果可以开辟另外一块长度为n的辅助空间时该怎么处理,显然只要对n个元素做n次(不放回的)随机抽取就可以了。
先从n个元素中任选一个,放入新空间的第一个位置,然后再从剩下的n-1个元素中任选一个,放入第二个位置,依此类推。
按照同样的方法,但这次不开辟新的存储空间。第一次被选中的元素就要放入这个数组的第一个位置,但这个位置原来已经有别的(也可能就是这个)元素了,这时候只要把原来的元素跟被选中的元素互换一下就可以了。很容易就避免了辅助空间。
void Random(std::vector<int>& num) { srand(time(NULL)); for (int i = num.size() - 1; i >= 0; --i) { int pos = rand() % (i + 1); std::swap(num.at(i), num.at(pos)); } }

6. 利用不均匀硬币产生等概率
问题描述:有一枚不均匀的硬币,已知抛出此硬币后,正面向上的概率为p(0 < p < 1)。请利用这枚硬币产生出概率相等的两个事件
某一次抛出硬币,正面向上的概率是p,反面向上的概率是1 - p,当p不等于0.5时,这两个事件的概率就不一样了。
怎么能凑出等概率呢?还是要利用概率的加法和乘法法则。这里用乘法,也就是连续的独立事件。
连续抛两次硬币,正反面的出现有四种情况,概率依次为:
两次均为正面:p * p 第一次正面,第二次反面:p * (1 - p) 第一次反面,第二次正面:(1 - p) * p 两次均为反面:(1 - p) * (1 - p)
中间两种情况的概率是完全一样的。于是问题的解法就是连续抛两次硬币,如果两次得到的相同则重新抛两次;
否则根据第一次(或第二次)的正面反面情况,就可以得到两个概率相等的事件
扩展:
这一题实质就是 利用不均匀概率事件 生成 [0,1]之间的随机数
如何利用 不均匀概率事件 生活[0,n)之间的随机数呢?(即0,1,2... n-1这n个数)
我们每一轮都是连续抛n次硬币
每一轮中 正面出现次数为i,则反面出现次数为 n-i,相应概率为 C(n, i) * (Pi) * (1-p)(n-i)
当i=1或者n-1时,上述概率分别为 n*p*(1-p)(n-1) 和 n*p(n-1)*(1-p)
注意到上面2个概率的系数都是n,我们现在需要随机生成n个数,我们就可以将这两点联系起来
例如i=1,对应n种情况,我们将这n种情况对应编号 n个数
对于每一轮中正面出现次数不是1的时候,就重新再抛一轮