先来道题:
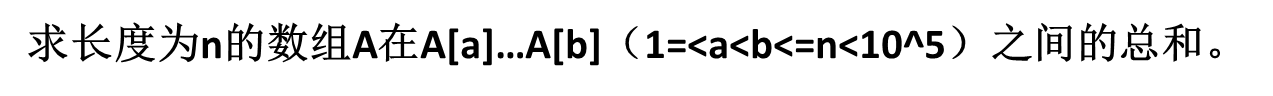
很简单,是吧(有脑子就行)
伪代码如下:
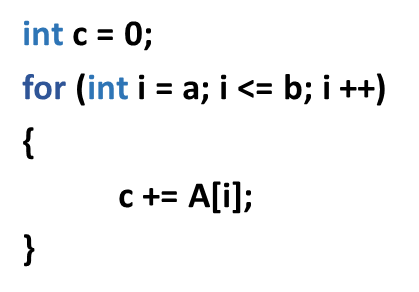
时间复杂度:(Theta(n))
但如果是求(q)((q<10^5))次连续和呢?
那这样做肯定TLE了
所以我们用前缀和来做:

比暴力快多了
但如果频繁修改(a[i])呢?
那前缀和肯定炸了
这里,我们引入一种新的算法:树状数组

这是树状数组
我们把它更直观的表示下——
这是原来的树:

我们把它右对齐:

这便是树状数组
再详细点:

(其中绿色为树状数组,红色为原数组)
我们令树状数组为(C),原数组为(a),利用上图不难发现:
(
C_1=a_1\
C_2=a_1+a_2\
C_3=a_3\
C_4=a_1+a_2+a_3+a_4\
C_5=a_5\
C_6=a_5+a_6\
C_7=a_7\
C_8=a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8
)
可以发现,这颗树是有规律的:
(C[i]=a[i-2^k+1]+a[i-2^k+2]+... +a[i];//k为i的二进制中从右往左第一位非0的位置)
那么问题来了:如何求(2^k)?
先给个结论:(2^k)=(i)&((-i))
咱们来看看Xenny大佬的解释:

于是可以写出代码:
int lowbit(int x)
{
return x&(-x);
}
有了以上基础,便可进入正题了(若不理解则多看几遍)
单点更新,区间查询
上面提到了:(C[i]=a[i-2^k+1]+a[i-2^k+2]+... +a[i])
那么如果我们更新某个(a[i])的值,则会影响到所有包含有(a[i])的(C数组)
稍微思考可知:(a[i])包含于(C[i+2^k]、C[(i+2^k)+2^k]...)
这便是更新和求和
如果你弄懂了上面的内容,代码应该也很好理解了:
int lowbit(int x)
{
return x&(-x);
}
void updata(int x,int y)//表示将a[x]+y
{
for(int i=x;i<=n;i+=lowbit(i))a[i]+=y;//更新
}
int getsum(int x)//表示a[1~x]的总和
{
int ans=0;
for(int i=x;i>=1;i-=lowbit(i))ans+=a[i];//求和
return ans;
}
所以区间 ((x,y)) 的值为 (getsum(y)-getsum(x-1))
更新和求和的时间复杂度:(Theta(log n))
练习题:
1
2
3
区间更新,单点查询
代码并不会变,只是多了个用差分建树
假设有个(a)数组:

我们要把(3)~(6)的数加(2),可直接将(a[3]+2,a[7]-2)
则(a)变为

这样要求每个值时,则只需让一个变量跑一遍累加即可
伪代码:
a[x]+=z;a[y+1]-=z;
for i:=1 to n do
sum+=a[i],
write(sum,' ');
把差分用到树状数组中便可打出如下代码:
void add(int l,int r,int x)//对l到r的数累加x,差分
{
update(l,x);update(r+1,-x);
}
练习:
1
参考资料
https://zhuanlan.zhihu.com/p/93795692
https://blog.csdn.net/bestsort/article/details/80796531
https://www.cnblogs.com/xenny/p/9739600.html
https://www.luogu.com.cn/blog/BotDand/shu-zhuang-shuo-zu-xue-xi-bi-ji
以及某人的PPT下载链接