最小生成树

0、前言

关于三种算法：
prim常用于稠密图，kruscal用于稀疏图，而prim堆优化在稀疏图中比kruskal跑得慢，在稠密图中用prim优化没多大必要？？？
模板代码戳这里

1、Prime算法

【算法思想】
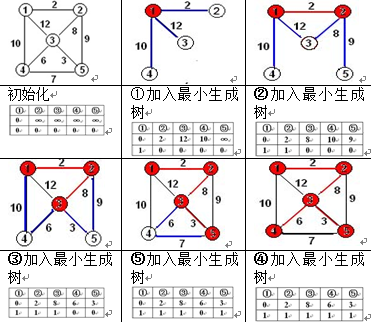
prim算法是一种贪心算法，最初将无向连通图G中所有顶点V分成两个顶点集合VA和VB。在计算过程中VA中的点为已经选好连接入生成树的点，否则属于VB。最开始的时候VA只包含任意选取的图G中的一个点u，其余的点属于VB，每次添加一个VB中的点到VA，该点是集合VB到集合VA中距离最小的一个点。直到V个顶点全部属于VA，算法结束。显然出发点不同，最小生成树的形态就不同，但边权和的最小值是唯一的。
【算法步骤】
选定图中的任意一个顶点V0，从V0开始生成最小生成树：
1.初始化dist[v0]=0，其他点的距离值dist[i]=∞。其中dist[i]表示集合VB中的点到VA的距离值。
2.经过N次如下步骤操作，最后得到一棵含N个顶点，N-1条边的最小生成树：

A.选择一个未标记的点k，并且dist[k]的值是最小的；
B.标记点k进入集合VA；
C.以k为中间点，修改未标记点j，即VB中的点到VA的距离值；

3.最后得到最小生成树T。
下面图为从顶点1开始生成最小生成树的过程：

【核心代码】

邻接矩阵

void Prim(int v0)
{  int i,j,k,minn;
   memset(vst,0,sizeof(vst));  //初始化生成树点集合
   for(i=1;i<=n;i++)d[i]=INF;d[v0]=0;
   ans=0;
   for(i=1;i<=n;i++) //选择n个点
   {  minn=INF;
      for(j=1;j<=n;j++)//选择最小边
         if(vst[j]==0 && minn>d[j]){minn=d[j];k=j;}
      vst[k]=1;  //标记
      ans+=d[k];
      for(j=1;j<=n;j++)   //修改d数组
          if(vst[j]==0&&d[j]>g[k][j])d[j]=g[k][j];
   }
}

邻接表

void Prim(int v0)
{  int i,j,y,k;
   for(i=1;i<=N;i++)d[i]=INF;d[v0]=0;//初始化d数组
   ans=0;
   for(i=1;i<=N;i++)
   {  minn=INF;
      for(j=1;j<=N;j++)if(!vst[j]&&minn>d[j]){k=j;minn=d[j];}//选
      ans+=d[k];  //累加最小生成树的边值
      vst[k]=1;  //标记顶点y被选入最小生成树
      for(j=h[k];j;j=a[j].next) //修改
      {  y=a[j].to; 
         if(!vst[y]&&a[j].v<d[y])d[y]=a[j].v; 
      }
   }
}

2、Kruskal算法

【算法思想】
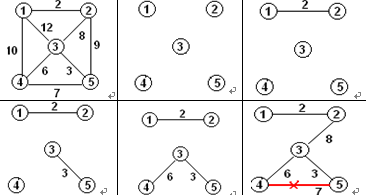
Kruskal算法也是一种贪心算法，它是将边按权值排序，每次从剩下得边集中选择权值最小且两个端点不再同一集合得边加入生成树中，反复操作，直到加入了n-1条边。
【算法步骤】

1.将边按权值从小到大快排；
2.按照权值从小到大依次选边。若当前选取的边加入后使生成树T形成环，则舍弃当前边；否则标记当前边并计数。
3.重复2的操作，直到生成树T中包含n-1条边为止。否则当遍历完所有的边后，都不能选取n-1条边，表示最小生成树不存在。
下面给出了的kruskal算法的执行过程图：

【核心代码】

void kruskal()//kruskal核心程序
{  int f1,f2,k,i;
   k=0;
   for(i=1;i<=n;i++)prt[i]=i;//初始化
   for(i=1;i<=m;i++)  
   {  f1=Getfather(a[i].x);f2=Getfather(a[i].y); //并查集 查找祖先
      if(f1!=f2)
      {  ans=ans+a[i].z;
         prt[f1]=f2;  //合并不相同的两个集合
         k++;
         if(k==n-1)break;  
      } 
   } 
   if(k<n-1){cout<<"Impossible"<<endl;bj=0;return;}
}

3、堆优化prim算法

【算法思想】
类似堆化dijsktra，发现prim算法中选择n-1条边需要执行n-1次，实质每次选最小的边，由此我们想到“小根堆”的性质。
【算法步骤】
用小根堆优化prim算法有以下几点：

1.初始化d数组和堆，并建立堆结点与d数组元素的对应关系表；
2.每次选择最小边的时候，直接取堆的根，然后将根结点值修改成INF，向下调整堆（down(k,m)；
3.修改d数组的值的时候，同时要修改d数组元素对应堆中结点的值，因为始终是将这个变小，所以向上调整堆up(k)。

这样优化后，得到的算法时间复杂度是：O(nlogn)
下面图示是依次“选最小边”后堆的调整：

选最小边：直接取堆的根接点，然后将根结点值修改成INF，向下调整堆 down(k,m)；

由上面的图示过程可知：堆的两种操作“向上、向下调整”导致堆中的结点与d数组中结点不对应，因此建立双向映射：

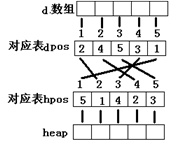
双向映射
设dpos[i]：表示数组中的第i个元素对应在堆中的位置为dpos[i]；
hpos[i]：表示堆中的第i个元素对应数组中的位置为hpos[i]；

【核心代码】

手写堆

void Heapdown()
{  int i=1,j; 
   while(i*2<=N)
   {  if(i*2==N||Heap[i*2]<Heap[i*2+1])j=i*2;else j=i*2+1;
      if(Heap[i]>Heap[j])
      {  swap(Heap[i],Heap[j]);
         swap(Hpos[i],Hpos[j]);
         swap(Dpos[Hpos[i]],Dpos[Hpos[j]]);//修改数组中的位置
         i=j;     
      }
      else break;
   }
}
void Heapup(int i)
{  while(i>1&&Heap[i]<Heap[i/2])
   {  swap(Heap[i],Heap[i/2]);
      swap(Hpos[i],Hpos[i/2]);
      swap(Dpos[Hpos[i]],Dpos[Hpos[i/2]]);
      i=i/2;
   }
}
void Prim()
{  int i,k,x,y,pos;
   for(i=1;i<=N;i++) Dpos[i]=i,Hpos[i]=i,Heap[i]=INF;
   Heap[1]=0;
   for(i=1;i<=N;i++) 
   {  Ans+=Heap[1];Heap[1]=INF;
      x=Hpos[1];vst[x]=1;
      Heapdown();
      for(k=First[x];k;k=a[k].next)
      {  y=a[k].to; 
         pos=Dpos[y];
         if(!vst[y]&&a[k].v<Heap[pos]) Heap[pos]=a[k].v,Heapup(pos);
      }
   }
}

//make_pair(dist值，编号) 相当于结构体，不会请自行搜索
void prim()
{
    memset(dist,0x7f,sizeof(dist)); dist[1]=0;
    cnt=0;
    q.push(make_pair(0,1));
    while(!q.empty()&&cnt<n)
    {
        int d=q.top().first,u=q.top().second;
        q.pop();
        if(flag[u]) continue;
        ++cnt; ans+=d; flag[u]=1;
        for(int i=head[u];i;i=e[i].next)
            if(e[i].w<dist[e[i].to]) dist[e[i].to]=e[i].w,q.push(make_pair(e[i].w,e[i].to));
    }
}