支持向量机(support vector machine, svm)在小样本、非线性、高维模式识别问题中有很多优势,并且能够方便地扩展到函数拟合等其他机器学习问题中。
1. svm思想
- 将低维空间中线性不可分的数据通过kernel trick映射到高维空间中,使得数据变得线性可分,从而实现分类;
- 寻找一个分割平面,使得两类数据距离这个平面最近的点到这个平面的距离相等且最大,这个平面即为所求分离超平面。
2. svm简单推导(适用于面试时手推公式)
svm的详细原理介绍及推导可见参考3(写的真的好,深入浅出),此处仅为面试时手推公式用的简洁版推导。

图片来源于参考3
如上图所示有两类样本,其中圆形样本的标签为(y=+1),正方形样本的标签为(y=-1)。设所求超平面的方程为:
其中(w,x)均为向量,(b)是标量。在上图中所求超平面即为中间的直线(H)。我们定义某个样本点(x_i)到超平面的距离为:
其中(y_i)是样本点(x_i)的标签,是个标量。容易知道(y_i(w^Tx_i+b))总是大于0的(应为若(y_i=+1),表明样本点(x_i)属于此类样本,则(w^Tx_i+b>0),同理,若(y_i=-1),则(w^Tx_i+b<0)),因此它的值就等于(|g(x_i)|)。我们对间隔( ho_i)进行归一化,得到几何间隔(delta_i):
在上图中,(H)是分类面,(H_1),(H_2)平行于(H),且过离(H)最近的两类样本。(H_1)到(H),(H_2)到(H)的距离即为几何间隔。我们的目标是最大化几何间隔,通常我们是固定间隔(g(x)),将其固定为1,然后寻找最小的(||w||)。于是我们将目标函数定义为:
为了后续计算方便,我们将目标函数改写为:
另外我们还要加入约束条件。前面说到我们把间隔(|g(x)|)固定为1,则对于其他样本点,他们都应该在间隔外面。因此有:
综上,我们的优化问题变为求解以下函数:
回顾一下,我们的目标是要求一个最优的超平面方程(g(x)=w^Tx+b=0),要求这个最优的超平面方程,就是要求出参数向量(w)(参数b在求出了参数(w)后只要带入几个支持向量样本即可求得,支持向量就是落在(H_1),(H_2)上的样本点)。其实向量(w)只与支持向量及其标签有关,因此(w)可以表示如下:
其中(x_1,...,x_t)是(t)个支持向量,(alpha_1,...,alpha_t)是系数,也叫做拉格朗日乘子,(y_1,...,y_t)是支持向量对应的标签。(w)也可以表示如下:
(g(x))的表达式可以改为:
其中(<cdot>)表示内积,(k(cdot))表示核函数。要求超平面方程,我们就是要求(g(x)),要求(g(x)),就是要求(alpha_i(i=1,...,t))。
因为有离群点(对于正样本,即为(H_1)左边的点,对于负样本,即为(H_2)右边的点)的存在,我们引入松弛变量(gamma),则目标函数改为如下:
其中(C)为惩罚因子,(C)越大,表示对离群点越重视,表示你非常不愿意放弃这些离群点。非离群点对应的松弛变量为0。松弛变量越大,表示离群点偏离得越远。
3. 核方法的思想
核方法的主要思想是基于这样一个假设:低维空间中线性不可分的点集在高维空间就变得线性可分了,如下图所示:
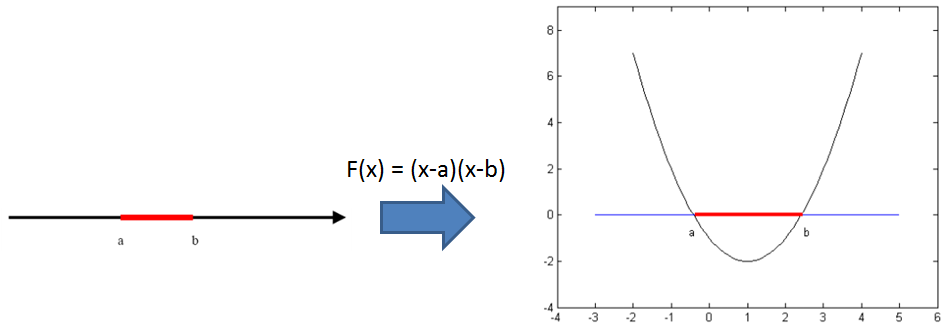
图片来源于网络
那么怎么将低维空间的点映射到高维空间呢?通过核技巧可以巧妙地解决这个问题。
高维空间中向量的乘积只要通过低维空间中点的核函数就可以计算,这种方法成为核技巧(kernel trick)。即只要在低维空间中计算两个点的核函数,我们就相当于得到这两个点在高维空间的内积。公式表达如下:
其中(k(cdot))是核函数,(x_1,x_2)是低维空间中的两个点,(phi(x_1),phi(x_2))是(x_1,x_2)在高维空间中的向量表示,(<phi(x_1),phi(x_2)>)表示的是高维向量(phi(x_1))和(phi(x_2)的内积。
4. 常用的核函数
线性核:
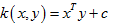
多项式核:
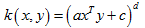
径向基核函数(Radial Basis Function):

高斯核函数:

Reference: