Mergeable heaps
A mergeable heap is any data structure that supports the following five operations,
in which each element has a key:
MAKE-HEAP./ creates and returns a new heap containing no elements.
INSERT.H; x/ inserts element x, whose key has already been filled in, into heap H.
MINIMUM.H/ returns a pointer to the element in heap H whose key is minimum.
EXTRACT-MIN.H/ deletes the element from heap H whose key is minimum, returning
a pointer to the element.
UNION.H1;H2/ creates and returns a new heap that contains all the elements of
heaps H1 and H2. Heaps H1 and H2 are “destroyed” by this operation.
In addition to the mergeable-heap operations above, Fibonacci heaps also support
the following two operations:
DECREASE-KEY.H; x; k/ assigns to element x within heap H the new key
value k, which we assume to be no greater than its current key value.1
DELETE.H; x/ deletes element x from heap H.


Each node has two other attributes. We store the number of children in the child
list of node x in x:degree. The boolean-valued attribute x:mark indicates whether
node x has lost a child since the last time x was made the child of another node.
Newly created nodes are unmarked, and a node x becomes unmarked whenever it
is made the child of another node. Until we look at the DECREASE-KEY operation
in Section 19.3, we will just set all mark attributes to FALSE.


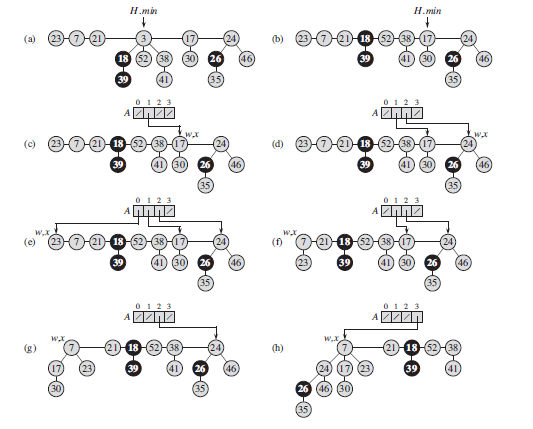
In detail, the CONSOLIDATE procedure works as follows. Lines 1–3 allocate
and initialize the array A by making each entry NIL. The for loop of lines 4–14
processes each root w in the root list. As we link roots together, w may be linked
to some other node and no longer be a root. Nevertheless, w is always in a tree
rooted at some node x, which may or may not be w itself. Because we want at
most one root with each degree, we look in the array A to see whether it contains
a root y with the same degree as x. If it does, then we link the roots x and y but
guaranteeing that x remains a root after linking. That is, we link y to x after first
exchanging the pointers to the two roots if y’s key is smaller than x’s key. After
we link y to x, the degree of x has increased by 1, and so we continue this process,
linking x and another root whose degree equalsx’s new degree, until no other root
that we have processed has the same degree as x. We then set the appropriate entry
of A to point to x, so that as we process roots later on, we have recorded that x is
the unique root of its degree that we have already processed. When this for loop
terminates, at most one root of each degree will remain, and the array A will point
to each remaining root.
The while loop of lines 7–13 repeatedly links the root x of the tree containing
node w to another tree whose root has the same degree as x, until no other root has
the same degree. This while loop maintains the following invariant:
At the start of each iteration of the while loop, d D x:degree.