对于一个多项式,如果我们能等到n个点值,就能求出多项式的各个系数
所以对于$F(x) = f(x) * g(x)$, 可以通过求出n个f(x)的值进而求出F(x)的系数
我们令这n个点分别为$ω_n^0, ω_n^1, ω_n^2 .... ,ω_n^n - 1$
$$f(ω_n^k) = sumlimits_{i = 0}^{n - 1}a_i *ω_n^{ki} = sumlimits_{i = 0}^{frac{n}{2} - 1}a_{2i} *ω_n^{2ki}+ω_n^{k}sumlimits_{i = 0}^{frac{n}{2} - 1}a_{2i + 1} *ω_n^{2ki}$$
$$=sumlimits_{i = 0}^{frac{n}{2} - 1}a_{2i} *ω_{frac{n}{2}}^{ki}+ω_n^{k}sumlimits_{i = 0}^{frac{n}{2} - 1}a_{2i + 1} *ω_{frac{n}{2}}^{ki}$$
而对于$f(ω_n^{k + frac{n}{2}})$
$$f(ω_n^{k + frac{n}{2}}) = sumlimits_{i = 0}^{n - 1}a_i *ω_n^{{(k+ frac{n}{2}})i} = sumlimits_{i = 0}^{frac{n}{2} - 1}a_{2i} *ω_n^{2ki}+ω_n^{k + frac{n}{2}}sumlimits_{i = 0}^{frac{n}{2} - 1}a_{2i + 1} *ω_n^{2ki}$$
$$=sumlimits_{i = 0}^{frac{n}{2} - 1}a_{2i} *ω_{frac{n}{2}}^{ki}- ω_n^{k}sumlimits_{i = 0}^{frac{n}{2} - 1}a_{2i + 1} *ω_{frac{n}{2}}^{ki}$$
于是发现
$$f(ω_n^k) = u + v$$
$$f(ω_n^{k + frac{n}{2}}) = u - v$$
然后发现求出点值后,直接求逆就能得到多项式的系数,就像下面的图片所述。。。
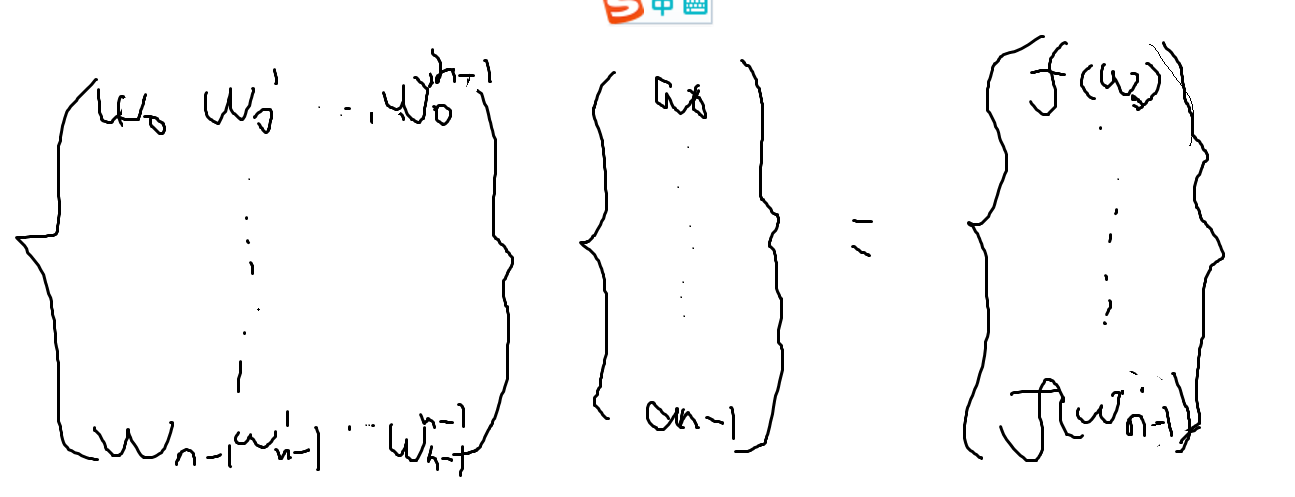
而u和v我们可以用同样的方法递归求解 这样是均摊(logn)的
当然FFT是递归的常数是很大的,所以我们可以先预处理出来,这个学一学模板就好了
有一个关于这个操作很详细的解释 补充——FFT中的二进制翻转问题
至于NTT,如果模数是一个2 ^ n * k + 1之类的数,例如998244353, 我们可以令$ω_n^k = 3^{frac{p - 1}{n}k}$,剩下的操作是相同的。
学会了理论,板子背一下就好了。 板子见下 :

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cmath> 5 #include <complex> 6 #include <algorithm> 7 #define LL long long 8 #define pi acos(-1) 9 #define E complex<double> 10 11 using namespace std; 12 13 const int MAXN = 5e6 + 10; 14 15 inline LL read() 16 { 17 LL x = 0, w = 1; char ch = 0; 18 while(ch < '0' || ch > '9') { 19 if(ch == '-') { 20 w = -1; 21 } 22 ch = getchar(); 23 } 24 while(ch >= '0' && ch <= '9') { 25 x = x * 10 + ch - '0'; 26 ch = getchar(); 27 } 28 return x * w; 29 } 30 31 E a[MAXN], b[MAXN]; 32 int n, m, L; 33 int R[MAXN]; 34 35 void FFT(E *a, int f) 36 { 37 for(int i = 0; i < n; i++) { 38 if(i < R[i]) { 39 swap(a[i], a[R[i]]); 40 } 41 } 42 for(int i = 1; i < n; i <<= 1) { 43 E wn(cos(pi / i), f * sin(pi / i)); 44 for(int p = i << 1, j = 0; j < n; j += p) { 45 E w(1, 0); 46 for(int k = 0; k < i; k++, w *= wn) { 47 E x = a[j + k], y = w * a[j + k + i]; 48 a[j + k] = x + y, a[j + k + i] = x - y; 49 } 50 } 51 } 52 } 53 54 int main() 55 { 56 n = read(), m = read(); 57 for(int i = 0; i <= n; i++) { 58 a[i] = read(); 59 } 60 for(int i = 0; i <= m; i++) { 61 b[i] = read(); 62 } 63 m = n + m; 64 for(n = 1; n <= m; n <<= 1) { 65 L++; 66 } 67 for(int i = 0; i < n; i++) { 68 R[i] = ((R[i >> 1] >> 1) | ((i & 1) << (L - 1))); 69 } 70 FFT(a, 1), FFT(b, 1); 71 for(int i = 0; i < n; i++) { 72 a[i] = a[i] * b[i]; 73 } 74 FFT(a, -1); 75 for(int i = 0; i <= m; i++) { 76 printf("%d ", (int)(a[i].real() / n + 0.5)); 77 } 78 return 0; 79 }
