LinearRegression 拟合一个带有系数w=(w1,...,w2)的线性模型使得数据集实际观测数据和预测数据(估计值)之间的残差平方和最小。其数学表达式为:
LinearRegression 会调用 fit 方法来拟合数组 X,y,并且将线性模型的系数 w 存储在其成员变量 coef_中:
from sklearn.linear_model import LinearRegression
line_reg = LinearRegression()
line_reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
print("Coefficient: {}".format(line_reg.coef_))
Coefficient: [0.5 0.5]
对于普通最小二乘的系数估计问题,其依赖于模型各项特征之间的相互独立性。当各项是相关的,且设计矩阵(design matrix)X 各列近似线性相关,那么,设计矩阵会趋向于奇异矩阵,这会导致最小二乘估计对于随机误差非常敏感,产生很大的方法。例如,在没有实验设计的情况下收集到的数据,多重共线性(multicollinearity)的情况可能真的会出现。
下面动手实现一个线性回归案例
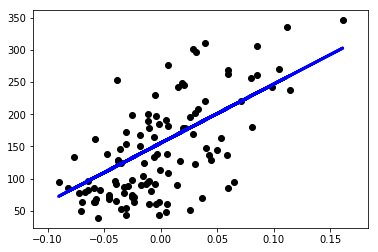
此示例仅使用糖尿病(diabetes)数据集的第一个特征,以说明此回归技术的二维绘图。在图中可以看到直线,显示了线性回归如何试图绘制一条直线,使数据集中观察到的响应与线性近似预测的响应之间的残差平方和最小化。
系数(The coefficents),残差平方和(the residual sum of squares)和方差得分(the variance score)也被计算出来了。
print(__doc__)
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
# 加载diabetes 数据集
diabetes = datasets.load_diabetes()
# 仅使用第一个特征
diabetes_X = diabetes.data[:, np.newaxis, 2]
# 把数据划分成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(diabetes_X, diabetes.target)
# 实例化一个 线性回归 类的对象
line_reg = linear_model.LinearRegression()
# 在训练集上训练模型
line_reg.fit(X_train, y_train)
# 在测试集上进行预测
prediction = line_reg.predict(X_test)
# 线性模型的系数
print("Coefficients: {}".format(line_reg.coef_))
# 均方误差
print("Mean squared error: {:.2f}".format(mean_squared_error(y_test, prediction)))
# 解释方法: 1 代表完美预测
print("Variance score: {:.2f}".format(r2_score(y_test, prediction)))
# 绘制输出结果
plt.scatter(X_test, y_test, color='black')
plt.plot(X_test, prediction, color='blue', linewidth=3)
plt.xticks()
plt.yticks()
Automatically created module for IPython interactive environment
Coefficients: [916.90503874]
Mean squared error: 3464.58
Variance score: 0.40
(array([ 0., 50., 100., 150., 200., 250., 300., 350., 400.]),
<a list of 9 Text yticklabel objects>)