在探讨核方法的本质之前,想先谈论一下机器学习中的坐标变换coordinate transformation。
曾经在看到陈平教授讲解物理在经济学模型上的应用的公开课视频时,听到他的一句总结:“现在物理模型大部分在做的其实都是同一件事情,就是坐标变换。从一个规律不明显不方便总结的坐标系,变换到另一个容易分析的坐标系,使得新坐标系内的数学公式的表达更精简更优美。”
我想,这句话放在机器学习里也是同样精辟的。最典型的就是SVM里的核函数进行坐标空间变换,以及神经网络里一层又一层的马尔科夫链形态的坐标空间变换。所谓横看成岭侧成峰,如果不把坐标系变换到侧面去看,恐怕也没有办法发现能够激活softmax分类器上代表某个分类的神经元的山峰吧。
所谓降维,无论PCA还是LLE又或是基于神经网络的方法(例如autoencoder),实际上都是在坐标空间内寻找一个比较好的低维内嵌流形。而这个“好”的指标,有的是保证所有点到流形表面的垂直距离平方和最小,有的是要让变换前后任意一个样本点与它临近的样本点的距离尽量保持不变,还有的是要让后面的cost最小化。不同目标,需求不同而已。
要描述坐标变换,需要用到黎曼几何。接下来一篇博文会对核方法以及常见的高斯核进行深度解读,所以先对黎曼几何涉及到的数学描述进行背景知识介绍。
定义坐标系X=(x, z)与X'=(q, r),简单起见,两个坐标系都是二维,先暂时回避流形以及降维的概念。
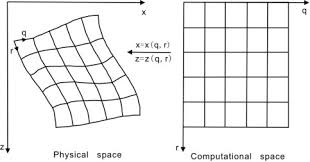
可以找到${ m{X}} o X'$的映射函数:
q(x, z)
r(x, z)
结合之前神经网络拟合任意函数的知识,需要至少2隐藏层sigmoid或是4层relu构成的逻辑门。如果output层神经元个数比输入层多,则构成升维。如果output神经元个数比较少,则构成降维。
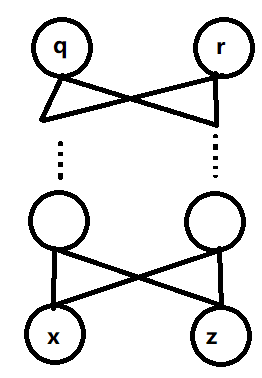
在样本空间X内,两个样本坐标之间的距离满足勾股定理:
[d{s^2} = d{x^2} + d{z^2}]
想象两个样本在二维空间内的位置是固定的,它们是空间内两个被固定住的拉平了的橡皮膜上的点。
接下来需要在橡皮膜上画出X坐标系,也就是常见的欧式坐标,则每个样本可以使用两个数字x、z来确定它在该坐标系内的唯一位置。在橡皮膜上画出的连接两点的直线的长度代表了在该坐标系内的距离。
再之后,擦去X坐标系,重新画出另一套曲面坐标系X',之后任意拉伸扭曲橡皮膜,形成一套曲线坐标。每个样本也同样可以通过坐标轴上均匀间隔的刻度上两个数字q、r来确定唯一位置。然而因为两点在空间内位置从头到尾都是被固定住的,所以存在一个不变的距离,这个距离不依赖使用哪一套坐标系来测量,长度是$intlimits_{p1}^{p2} {ds} $ , p1和p2分别是两个点。截取任意小一段距离ds,定义度量距离公式$d{s^2}$。
度量距离$d{s^2}$的泛化描述是
$d{s^2} = sumlimits_{i,j = 1..2} {{{ m{g}}_{ij}}d{X_i}d{X_j}} = sumlimits_{i,j = 1..2} {{{ m{g’}}_{ij}}d{X’_i}d{X’_j}} $
${ m{d}}{X_1} = dx$
${ m{d}}{{ m{X}}_2} = dz$
${ m{d}}{X'_1} = dq$
${ m{d}}{{ m{X'}}_2} = dr$
这里用X_1与X_2来代表X下的两个坐标x与z,统一标识方便使用sum符号。基于同样的理由,也使用X'_1与X'_2来分别代表X'下的q和r。
${{
m{g}}_{ij}}$ 是度量张量,当该张量 =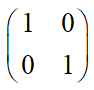 时,度量距离公式简化成勾股定理,描述的空间是二维欧式空间。
时,度量距离公式简化成勾股定理,描述的空间是二维欧式空间。
当度量张量 = 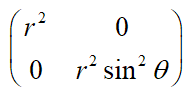 时, 描述的是二维极坐标。
时, 描述的是二维极坐标。
根据链式原理:
[{ m{d}}X{'_a} = sumlimits_{i = 1,2} {frac{{partial X{'_a}}}{{partial {X_i}}}{dX_i}} ]
带入度量距离invariant公式之后对比g'与g,得到:
[g{'_{ab}} = sumlimits_{i,j} {{g_{ij}}frac{{partial {{ m{X}}_i}}}{{partial X{'_a}}}frac{{partial {{ m{X}}_j}}}{{partial X{'_b}}}} ]
对于任意一个满足局部正交基的坐标系,勾股定理得到满足,且只有当a=b时,g_ab 不等于0。
那么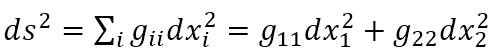
让ds横跨一块极小长方形面积的对角线,可得垂直的两条边长分别是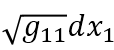 与
与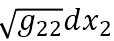
面积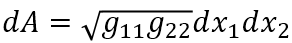
实际上不仅对于二维正交坐标系上述式子成立,对于更高维度(n维)的任意几何空间,
 也成立,这里不予证明。
也成立,这里不予证明。
所以度量张量g里面元素的大小实质上决定了在经历坐标变换之后,一小块单位面积被扭曲拉伸或是压缩之后得到的新的区域的面积。
可以理解为平整橡皮膜上画一块小方块之后拉扯橡皮膜之后转化成的新的不规则面积,两者之间的比例由g里的元素决定。
计算dX'/dX时,中间层输出为u,坐标变换假如需要L层,除了最后一层满足
${{ m{u}}^{(L)}} = {mathop{ m Re} olimits} lu({w^{(L)}} cdot {u^{L - 1}} + {b^{(L)}}) = {mathop{ m Re} olimits} lu(X')$
,以及第一层满足${{ m{u}}^{(0)}} = X$以外,其它层满足递归:
[frac{{d{u_j}(x)}}{{dx}} = frac{{partial {mathop{ m Re} olimits} lu(sum olimits_{ m{i}} {w_i^{({ m{l}})} cdot { m{u}}_{ m{i}}^{(l - 1)} + {b^{(l)}}} )}}{{partial x}}{ m{ = }}sum olimits_{ m{i}} {{H_i}({u^{(l)}})w_i^{(l)} cdot frac{{d{ m{u}}_{ m{i}}^{(l - 1)}}}{{partial x}}} ]
其中H(x)是赫维赛德阶跃函数,这里H(x)的连乘主要起拼凑门控制的响应区域范围的作用。不同响应区域被不同的门激活,所以$frac{{d{u_j}(x)}}{{dx}}$在不同的x取值时能够得到不同的值,呈现非线性拟合函数的能力。
上式得到
[frac{{partial { m{X}}'}}{{partial X}} = {w^{(L)}}sumlimits_{{i_1},{i_2}...{i_L}} {prodlimits_l {{H_{{i_l}}}({u^{(l)}}){w_{{i_l}}}^{(l)}} } ]
可以看出所有层里权重w越大,dX'/dX也就越倾向于大数值。将变量扩展到多个维度上,dX'/dX → dXa'/dXi
结合之前推导出的$g{'_{ab}} = sumlimits_{i,j} {{g_{ij}}frac{{partial {{ m{X}}_i}}}{{partial X{'_a}}}frac{{partial {{ m{X}}_j}}}{{partial X{'_b}}}} $
在坐标变换之前${{ m{g}}_{ij}} = {delta _{ij}}$ = 1 if i=j else 0
坐标变换之后如果w普遍比较大,dXa'/dXi越大,dXi/dX'a 越小,所以新坐标系里g'ab也就越小,单位面积变换后也就被压缩得比较小,反之则是拉伸变换后的面积。
因为g'ab(X0', X1')=g'ab(q, r),不同区域获得的拉伸/压缩的比例不同,所以就如同橡皮膜一样,神经网络可以通过不同权重,达成坐标系非线性变换的效果。
把维度从二维扩展到任意维度,可以看出DNN是可以通过改变权重矩阵W来调整度量张量g,从而改变任意维度流形的几何性质,就如同对2D的橡皮膜、3D的橡皮块变形扭曲。同时线性函数也能够直接获得高维空间在低维空间内的投影,所以神经网络具有强大的坐标系变换能力,比SVM的核函数具有更好的灵活性,将数据所在的坐标系变换到分类器方便处理的空间内,最终完成分类任务,又或是将分类器替换成最小二乘Loss完成回归。