$0$ 概述
后缀数组是一种用来处理字符串问题的工具,代码量小,功能强大。
简单来说,一个字符串的所有后缀按字典序排序后的结果,就是这一个字符串的后缀数组。
求后缀数组的常见算法由两种,分别是$O(nlogn)$的倍增法和$O(n)$的$DC3$算法。
$DC3$算法虽然时间复杂度更优,但其常数不太优秀,也没有倍增法那么易于实现,所以本文介绍的是倍增法。
$1$ 基本概念与定义
子串:由一个字符串中连续的一段字符组成的字符串。
后缀:以字符串中最后一个字符为结尾的子串。
$Suffix(i)$:起始位置为$i$的后缀。
$SA(i)$:表示将一个字符串的所有后缀按字典序从小到大排序后,排在第$i$位的后缀的起始位置。
$Rank(i)$:表示以第$i$个字符为起始位置的后缀在被和其它所有后缀按字典序从小到大排序后的名次。
显然,$SA(Rank(i))=i$。
$SA$就是我们要求的后缀数组。
$2$ 排序其实也没那么简单
好,现在让我们来思考一下怎样给一个字符串的所有后缀排序。
直接提取后缀再快排显然是不可取的,比较两个后缀字典序大小的时间复杂度是$O(n)$级别的,太慢了。
我们需要换一个方向。
给一堆后缀排序,其实也是在给一堆字符串排序。先思考一个简单的问题,现在有$n$个字符串,每一个字符串的长度都是$2$,那么应该怎么在$O(n)$的时间内把它们按字典序从小到大排好序呢?
一种可取的思路是,先按每一个字符串第二个字符字典序的大小稳定排序,再按每一个字符串第一个字符字典序的大小稳定排序。
比如说有$3$个字符串:$ab$,$ac$,$cb$。
第一遍排序:$ab$,$cb$,$ac$。
第二遍排序:$ab$,$ac$,$cb$。
这样就排好了。
不过应该怎么实现呢?其实也很简单。
我们把刚刚那个例子转换成数字来看一看,也就是:$12$,$13$,$32$。
第一遍排序,先用一个桶$cnt$存储每种关键字出现的次数:
关键字: $1$ $2$ $3$
出现次数:$0$ $2$ $1$
然后做一遍前缀和,即按从小到大的顺序每一个位置都加上前一个位置的值:
关键字:$1$ $2$ $3$
值:$0$ $2$ $3$
此时,$cnt(i)$表示的意义就是当前关键字小于等于$i$的数有多少个。
然后我们再在原序列中从后往前为每一个数安排位置,我们用$w$数组来存储排序好的序列。
首先,我们处理第$3$个数$32$,它的关键字是$2$,$cnt(2)=2$,说明关键字小于等于$2$的数有$2$个,那么它的排名就是$2$,所以$w(2)=32$。
因为$32$已经放好了,所以$cnt(2)$--。
然后,我们处理第$2$个数$13$,它的关键字是$3$,$cnt(3)=3$,说明关键字小于等于$3$的数有$3$个,那么它的排名就是$3$,所以$w(3)=13$。
因为$13$已经放好了,所以$cnt(3)$--。
最后,我们处理第$1$个数$12$,它的关键字是$2$,$cnt(2)=1$,说明关键字小于等于$2$的数有$1$个,那么它的排名就是$1$,所以$w(1)=12$。
因为$12$已经放好了,所以$cnt(2)$--。
至此,我们就完成了第一遍排序。
为什么要从后往前扫呢?因为要稳定排序啊。
第二遍排序也同理,这里就不再赘述。
其实,这一种排序方法有一个名字,叫作基数排序。
基数排序也是倍增法的核心。
这一部分的代码实现如下(代码里排的是字符串):

int m=0;//m用来记录最大的关键字 //第一遍排序 memset(cnt,0,sizeof(cnt)); for(int i=1;i<=n;i++) cnt[s[i][2]]++,m=max(m,s[i][2]); for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1]; for(int i=n;i>=1;i--) w[cnt[s[i][2]]--]=i; //第二遍排序 memset(cnt,0,sizeof(cnt)); for(int i=1;i<=n;i++) cnt[s[i][1]]++,m=max(m,s[i][1]); for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1]; for(int i=n;i>=1;i--) w[cnt[s[i][1]]--]=i;
$3$ 倍增是一个好东西
刚刚说了一大堆,好像并没有什么用啊,我们还是不知道如何将一个字符串的所有后缀排序啊。
嗯,是的。所以,这时我们就需要用到倍增了。
首先,我们将每一个后缀按其第一个字符排序。
然后,我们将每一个后缀按其前两个字符排序。
接着,我们将每一个后缀按其前四个字符排序。
……
对于第$i$次排序,我们就将每一个后缀按其前$2^i$个字符排序,如果长度不够就默认为空,“空”是优先级最高的。
这样一来,我们就只需要排$logn$次了。
可是,每一轮排序我们应该如何操作呢?
考虑利用上一轮排序的信息。
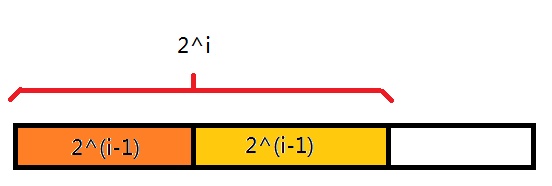
如图,现在正在进行第$i$轮排序,要将这一个后缀按前$2^i$个字符排序。
可以发现,在经过第$i-1$轮排序后,我们已经得出了前$2^i$字符中前半部分和后半部分的排名。
那么,我们就可以直接将前半部分和后半部分的排名分别作为这一个后缀前$2^i$个字符的第一关键字和第二关键字进行排序。
什么?第一关键字和第二关键字?只有两个关键字的排序?这一个问题我们刚刚不是解决过了吗?
是的,这就是倍增法的巧妙之处。它利用了前一次排序的结果,使得此时每一个后缀关键字的数量都减少为两个。
那么,我们就可以进行基数排序了!是$O(n)$的!
也就是说,我们可以用$O(nlogn)$的时间求出后缀数组!
嗯,没错。
代码实现如下:

//cnt是桶 //A[i]用来记录每轮排序中按第二关键字排序后,排在第i位的后缀的起始位置 //R是临时数组 //SA[i]用来记录每轮排序中按第一关键字排序后,排在第i位的后缀的起始位置 //Rank[i]用来记录每轮排序后,起始位置为i的后缀的名次 //st是原串 //当所有操作完成后,SA和Rank就是“基本概念与定义”中所描述的那两个数组了 int cnt[N],A[N],R[N],SA[N],Rank[N]; char st[N]; //首先对每一个后缀的第一个字符进行排序 //m用来记录最大的排名 for(int i=1;i<=n;i++) Rank[i]=int(st[i]),m=max(m,Rank[i]); for(int i=1;i<=n;i++) cnt[Rank[i]]++; for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1];//前缀和操作 for(int i=n;i>=1;i--) SA[cnt[Rank[i]]--]=i;//为每一个后缀安排位置 //开始倍增 for(int L=1;L<=n;L<<=1)//现在要对每一个后缀的前2*L个字符进行排序 { //按第二关键字排序 //由于上一轮的排序,起始位置为i的后缀的第二关键字就是Rank[i+L] //这时i+L可能大于原串长度,所以数组的大小要开原串长度的两倍 for(int i=0;i<=m;i++) cnt[i]=0;//清空桶 for(int i=1;i<=n;i++) cnt[Rank[SA[i]+L]]++; for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1]; for(int i=n;i>=1;i--) A[cnt[Rank[SA[i]+L]]--]=SA[i]; //按第一关键字排序 //由于上一轮的排序,起始位置为i的后缀的第一关键字就是Rank[i] for(int i=0;i<=m;i++) cnt[i]=0;//清空桶 for(int i=1;i<=n;i++) cnt[Rank[A[i]]]++; for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1]; for(int i=n;i>=1;i--) SA[cnt[Rank[A[i]]]--]=A[i]; //此时SA数组中存储的就是这一轮排序后,排在第i位的后缀的起始位置 //现在我们来求每一个后缀的名次是什么 //当一个后缀的第一关键字和第二关键字都与排在它前面的一个后缀相同时, //它的排名和前一个后缀也相同,否则其排名就为前一个后缀的排名加一 //Rank数组里就存有每一个后缀的关键字的大小 //所以我们不能改变Rank数组,要用一个临时数组R来存储每一个后缀的名次 //这一部分处理第二关键字时数组下标可能会大于原串长度, //所以数组的大小要开原串长度的两倍 R[SA[1]]=1;//排在第一位的后缀排名为一 for(int i=2;i<=n;i++) //如果当前后缀两个关键字都与前一个后缀相同,其排名也与前一个后缀相同 if(Rank[SA[i]]==Rank[SA[i-1]]&&Rank[SA[i]+L]==Rank[SA[i-1]+L]) R[SA[i]]=R[SA[i-1]]; else R[SA[i]]=R[SA[i-1]]+1;//否则为前一个后缀的排名加一 m=R[SA[n]];//更新最大排名 for(int i=1;i<=n;i++) Rank[i]=R[i];//更新Rank数组 //如果当前最大排名等于n,就说明现在任何两个后缀都没有相同的排名了 //也就是说,所有后缀的排名都已经确定了,再继续排也改变不了了 //所以当最大排名等于n时就可以直接跳出循环了 if(m==n) break; }
$4$ 优化是很重要的
考虑优化每轮排序中按第二关键字排序的部分。
想一想每轮排序中按第二关键字排序后排在最前面的是哪些后缀?
对,就是哪些没有第二关键字的后缀。
哪些后缀没有第二关键字?对,就是起始位置在$n-L+1$和$n$之间的后缀,因为这一些后缀的起始位置加$L$大于$n$,为“空”。
那么我们就只需把这些没有第二关键字的后缀加入数组里即可。
好,那么有第二关键字的后缀呢?
考虑利用上一轮排序留下来的信息。
我们可以从前到后遍历上一轮排序后的$SA$数组,如果$SA[i]>L$,就将$SA[i]-L$加入数组。
为什么呢?因为如果$SA[i]>L$,就说明$Suffix(SA[i])$是某一个后缀的第二关键字,即$Suffix(SA[i]-L)$的第二关键字。
经过上一轮排序后,$SA$数组已经是有序的了,所以对于两个位置$u$和$v$,$u<v$且$SA[u]>L$,$SA[v]>L$,那么按第二关键字排序时,$Suffix(SA[u]-L)$就一定排在$Suffix(SA[v]-L)$的前面,因为$Suffix(SA[u])$排在$Suffix(SA[v])$的前面嘛,而$Suffix(SA[u])$和$Suffix(SA[v])$又分别是$Suffix(SA[u]-L)$和$Suffix(SA[v]-L)$的第二关键字。
这样一来,我们就完成了按第二关键字排序的工作。
代码实现如下:

int cnt[N],A[N],R[N],SA[N],Rank[N]; char st[N]; for(int i=1;i<=n;i++) Rank[i]=int(st[i]),m=max(m,Rank[i]); for(int i=1;i<=n;i++) cnt[Rank[i]]++; for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1]; for(int i=n;i>=1;i--) SA[cnt[Rank[i]]--]=i; for(int L=1;L<=n;L<<=1) { int p=0; for(int i=n-L+1;i<=n;i++) A[++p]=i;//处理没有第二关键字的后缀 for(int i=1;i<=n;i++) if(SA[i]>L) A[++p]=SA[i]-L;//处理有第二关键字的后缀 for(int i=0;i<=m;i++) cnt[i]=0; for(int i=1;i<=n;i++) cnt[Rank[A[i]]]++; for(int i=1;i<=m;i++) cnt[i]+=cnt[i-1]; for(int i=n;i>=1;i--) SA[cnt[Rank[A[i]]]--]=A[i]; R[SA[1]]=1; for(int i=2;i<=n;i++) if(Rank[SA[i]]==Rank[SA[i-1]]&&Rank[SA[i]+L]==Rank[SA[i-1]+L]) R[SA[i]]=R[SA[i-1]]; else R[SA[i]]=R[SA[i-1]]+1; m=R[SA[n]]; for(int i=1;i<=n;i++) Rank[i]=R[i]; if(m==n) break; }
$5$ Height
其实,如果单单是求出后缀数组,即$SA$的话,用途还不太广泛。
但只要我们求出一个十分重要的东西:$Height$数组,我们就可以做很多事情了。
那么这一个$Height$数组究竟是一个什么东西,该怎么求呢?
先来看$Height$数组的定义:
$Height(i)$:表示将所有后缀按字典序从小到大排好序后,排在第$i$位的后缀和排在第$i-1$位的后缀的最长公共前缀的长度。
然后我们来看一下$Height$数组的一个性质:
排在第$x$位和排在第$y$位的两个后缀的最长公共前缀的长度为$min{Height(x+1),Height(x+2),....Height(y)}$。($x≤y$)
未完待续......
