题面:

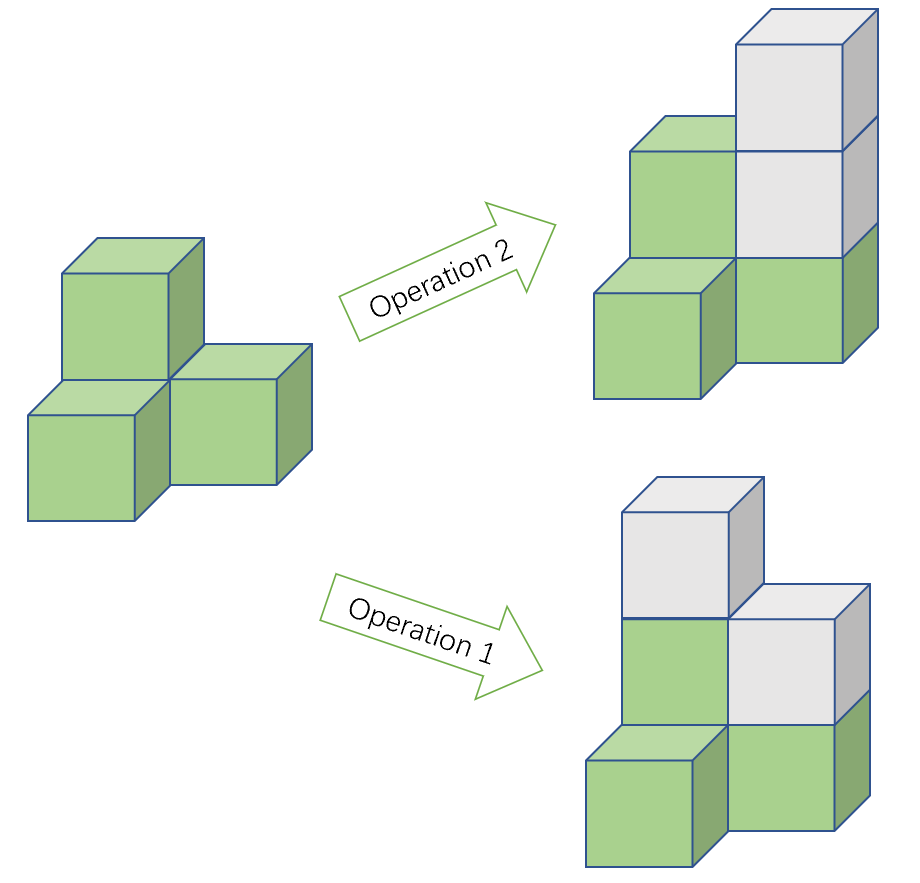
思路:
首先所有操作对于总和都是 (+2) ,因此总和的奇偶性质是不变的
那么考虑最终情况,假设为 (x) ,只要这个 (sum x) 的奇偶情况和初始一样,就一定存在方案达到这个结果
方案就是只需要每次选相邻 (+1+1) 直到 (x) ,或者选择单独的 (+2) ,实际上选择单独的 (+2) 相当于选了一个点 (+1) 和相邻的点 (+1) ,这个相邻的点就是他自己,也就是说 (+2) 和 (+1+1) 本质是相同的
考虑证明不会存在无解的情况:
若最终出现两个及以上的 (x-1) ,那么可以通过调整前面 (+1+1) 的对象,可以将这两个及以上的 (x-1) 放到一起,这样这些 (x-1) 又是相邻的,就可以继续使用 (+1+1) ;
若出现只有一个 (x-1) 的情况,那么总和就和设定的 (x) 的总和奇偶性质不同,但是一开始设定的 (x) 就是 (x) 总和和初始总和奇偶性质相同,出现矛盾,所以不存在这种情况
因此只需要 (n*m*x) 的奇偶性与 (sum a_{i,j}) 的奇偶性一样就一定存在方案
那么发现 (n*m) 为奇数的时候,不管 (sum a_{i,j}) 奇偶性如何,都存在 (x) 使得 (n*m*x) 的奇偶性与其一致
因此 (n*m) 为奇数时所有情况都是有解的,答案为 ((r-l+1)^{nm})
(n*m) 为偶数时,所有的 (x) 得到的 (n*m*x) 都是偶数,因此只有 (sum a_{ij}) 是偶数才有方案
下面用两种解释来解题
首先我们可以把 ([l,r]) 改为 ([0,r-l])
一、
设 (E) 为偶数个数, (O) 为奇数个数,则答案为 (sum_{i=0,i+=2}^{nm} C_{nm}^i E^i O^{nm-i})
容易看出这个是二项式定理,即为 (frac{(E+O)^{nm}+(E-O)^{nm}}{2})
二、
对于 (r-l) 为奇数,即 (r-l+1) 为偶数
此时对于一个和为偶数的情况,我们令 (a_{i,j}=a_{i,j} xor 1) ,此时该情况就变成了奇数的情况
因此对于 (r-l+1) 是偶数时,所有偶数情况都有其对应了奇数的情况,因此答案为 (frac{(r-l+1)^{nm}}{2})
对于 (r-l) 为偶数,即 (r-l+1) 为奇数
寻找配对的方法和上面类似,不过遇到当 (a_{i,j}=r-l) 时,这个值不变
容易发现存在一种情况即都为 (r-l) 的情况其对应的状态就是他本身,因此我们可以虚构一个状态来对应他,那么答案就是 (frac{(r-l+1)^{nm}+1}{2})
代码:
解法一、
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<stack>
#include<queue>
#include<vector>
#include<cstring>
#include<string>
#include<map>
#define ll long long
#define mod 998244353
using namespace std;
ll n,m,l,r,ans;
ll ppow(ll a,ll x)
{
ll tans=1;
while(x)
{
if(x&1)tans=tans*a%mod;
a=a*a%mod;x>>=1;
}
return tans;
}
int main()
{
scanf("%lld%lld%lld%lld",&n,&m,&l,&r);
if((n*m)&1)ans=ppow(r-l+1,n*m);
else ans=(ppow(r-l+1,n*m)+ppow((r-l+2)/2-(r-l+1)/2,n*m))*ppow(2,mod-2)%mod;
printf("%lld
",ans);
return 0;
}
解法二、
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<stack>
#include<queue>
#include<vector>
#include<cstring>
#include<string>
#include<map>
#define mod 998244353
#define ll long long
using namespace std;
int T;
ll ppow(ll a,ll x)
{
ll tans=1;
while(x)
{
if(x&1)tans=tans*a%mod;
a=a*a%mod;x>>=1;
}
return tans;
}
ll n,m,l,r,ans;
int main()
{
scanf("%lld%lld%lld%lld",&n,&m,&l,&r);
if((n*m)&1)ans=ppow(r-l+1,n*m);
else if((r-l+1)&1)ans=(ppow(r-l+1,n*m)+1)*ppow(2,mod-2)%mod;
else ans=ppow(r-l+1,n*m)*ppow(2,mod-2)%mod;
printf("%lld
",ans);
return 0;
}