欧拉phi函数,等于不超过X且和X互素的整数个数,公式如下:
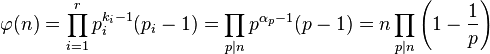
p1,p2......pn为X的所有素因数
欧拉公式的延伸:一个数的所有质因子之和是euler(n)*n/2
模板:
有趣的是欧拉函数的计算和素数判定很类似。单个欧拉函数可以用试除法,时间复杂度仍分别为O(pn)。
单个欧拉函数由刚才的讨论,只需要设置初始结果为n,然后对n做素因数分解,对于所有素因子p,乘以1-1/p =(p-1)/p即可。对于每次找到一个素因子之后把它“除干净”,即可保证找到的因子都是素数。
#include <stdio.h>
#include <math.h>
int euler_phi(int n) {
int m = (int)sqrt(n+0.5);
int ans = n;
for(int i=2; i <= m; i++)
if(n % i == 0){
ans = ans / i * (i-1); //由欧拉函数的性质三的说明可知
while(n % i == 0) n/= i; //每次找到一个素因子之后把它“除干净”
}
if(n >1) ans = ans / n * (n -1); //存在大于sqrt(n)的素因子
return ans;
}
int main() {
int n,total;
scanf("%d",&n);
total=euler_phi(n);
printf("
%d
",total);
}POJ2407(模板题)
链接:http://poj.org/problem?id=2407
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int euler_phi(int n)
{
int m=sqrt(n+0.5);
int ans=n;
for(int i=2;i<=m;i++)
if(n%i==0)
{
ans=ans/i*(i-1);
while(n%i==0)
n/=i;
}
if(n>1) ans=ans/n*(n-1);
return ans;
}
int main()
{
int n;
while(cin>>n)
{
if(n==0) break;
cout<<euler_phi(n)<<endl;
}
return 0;
}
链接:http://poj.org/problem?id=2773
此题虽然是欧拉函数题,但是任然可以用gcd来解,当时做的时候忽略了第k个数大于m的情况,所以一直在WA
题目大意就是给出n和k求出第k个与n互素的数
如果知道欧几里德算法的话就应该知道gcd(b×t+a,b)=gcd(a,b) (t为任意整数)
则如果a与b互素,则b×t+a与b也一定互素,如果a与b不互素,则b×t+a与b也一定不互素
故与m互素的数对m取模具有周期性,则根据这个方法我们就可以很快的求出第k个与m互素的数
假设小于m的数且与m互素的数有k个,其中第i个是ai,则第m×k+i与m互素的数是k×m+ai
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn=1000000+10;
int pre[maxn];
int gcd(int a,int b)
{
if(b==0) return a;
else
return gcd(b,a%b);
}
int main()
{
int n,k;
while(cin>>n>>k)
{
memset(pre,0,sizeof(pre));
int j=0;
for(int i=1;i<=n;i++)
if(gcd(n,i)==1)
pre[j++]=i;
if(k%j!=0)
cout<<k/j*n+pre[k%j-1]<<endl;
else
cout<<(k/j-1)*n+pre[j-1]<<endl;
}
return 0;
}
下面上欧拉函数的解决方法,本题记录欧拉函数路径,很值得学习,可以作为比较好的模板
对m求欧拉函数的同时对m进行分解,求出m的所有素因子,所有与m不互素的数,都至少与m有一个公共素因子,于是,我们可以在每次找到一个m的素因子后,将它的整数倍标记,这样,后面枚举的时候就可以用O(1)的时间判断了
#include <iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<map>
#include<vector>
using namespace std;
const int N=1000000;
int prime[801];//保存1000以内的素数
int num;//1000以内素数的个数
int isprime[1000001];
int flag[1000001];//flag[i]表示i是否与当前m互质
void getprime()//筛出素数
{
for(int i=2;i<=1000000;i++)if(isprime[i]==0)
{
prime[num++]=i;
for(int j=1;j*i<=1000000;j++)
isprime[j*i]=1;
}
}
int euler(int n)//求出n的欧拉函数并且筛出所有与其互质的数flag[i]==0表示n与i不互质
{
int nn=n;
int res=n;
for(int i=0;i<num&&prime[i]*prime[i]<=n;i++)
{
if(n%prime[i]==0)
{
res=res/prime[i]*(prime[i]-1);
while(n%prime[i]==0)
{
n/=prime[i];
}
for(int j=prime[i];j<=nn;j=j+prime[i])//所有prime[i]的倍数肯定与n不互质
{
flag[j]=1;
}
}
}
if(n>1)
{
res=res/n*(n-1);
for(int j=n;j<=nn;j+=n)
{
flag[j]=1;
}
}
return res;
}
int solve(int key)
{
int cnt=0;
for(int i=1;i<=1000001;i++)
{
if(flag[i]==0)
cnt++;
if(cnt==key)
return i;
}
}
int main()
{
int m,k;
getprime();
while(scanf("%d%d",&m,&k)!=EOF)
{
memset(flag,0,sizeof(flag));
if(m==1)
{printf("%d
",k);continue;}
int f=euler(m);
int key=(k-1)%f+1;
printf("%I64d
",(__int64)((k-1)/(f)*m+solve(key)));
}
}
二.求单个欧拉函数和函数表,计算phi(i)
另外,如果需要求1~n的所有欧拉函数值,可以用与筛法求素数非常类似的方法,求出一个素数p后,它对所有倍数2p、3p、…,都有(p-1)/p的贡献,用一个循环即可完成求解。初始设所有φ值为0,因此如果再累乘时发现一个0值,先初始化为n,再乘以(p-1)/p。另外由于还没有被筛过的数φ值为0,因此这同时也是素数标志。求1~n的所有欧拉函数值的时间复杂度为O(nloglogn)。
模板:
void phi_table(int n)
{
for(int i=2;i<=n;i++)
phi[i]=0;
phi[1]=1;
for(int i=2;i<=n;i++)
if(!phi[i])
for(int j=i;j<=n;j+=i)
{
if(!phi[j])
phi[j]=j;
phi[j]=phi[j]/i*(i-1);
}
}题目:POJ2478
链接:http://poj.org/problem?id=2478
题目大意就是求Fi集合中元素的个数,其中Fi集合的元素满足下列条件
形如a/b,且0<a<b<=i, gcd(a,b)=1
很明显,这题就是欧拉公式的运用,关于欧拉公式可查看下这篇文章
http://www.cnblogs.com/ACShiryu/archive/2011/08/04/poj2407.html
对于这题,可以先求出以每一个小于m的数为分母的数的个数,即也是与该数互素的数的个数,也就是求的phi[i];
然后再每一个phi都加起来
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn=1000005;
int phi[maxn];
void phi_table(int n)
{
for(int i=2;i<=n;i++)
phi[i]=0;
phi[1]=1;
for(int i=2;i<=n;i++)
if(!phi[i])
for(int j=i;j<=n;j+=i)
{
if(!phi[j])
phi[j]=j;
phi[j]=phi[j]/i*(i-1);
}
}
int main()
{
int n;
phi_table(maxn);
while(scanf("%d",&n)!=EOF)
{
if(n==0) break;
long long sum=0;
for(int i=2;i<=n;i++)
sum+=phi[i];
printf("%lld
",sum);
}
return 0;
}