APIO2010
APIO2010T1 特别行动队
记 (dp[i]) 表示划分前 (i) 个时的答案,则有 (dp[i] = max{ dp[j] + a(sum[i]-sum[j])^2+b(sum[i]-sum[j])+c | 0le j< i})
若 (p<q) ,且满足 (2a imes sum[i] imes (sum[q]-sum[p])<=(a imes sum[q]^2-b imes sum[q]+dp[q])-(a imes sum[p]^2-b imes sum[p]+dp[p])) ,则由于 (a<-1 且 sum[i]<sum[i+1]) ,所以 (LHS) 变小,(p) 一定不会比 (q) 优,弹出队列。
时间复杂度:(O(n))
APIO2010T2 巡逻
对于一棵树,每条边一定走 (2) 遍。
当 (k=1) :我们发现把树的直径给连成环以后,减少的贡献最大,答案最小。
当 (k=2) :无非找两次直径连成环,但这环可能会重叠,怎么办?
有一个很方便的做法,就是第一次跑完直径后,给直径上的所有边权乘以 (-1) ,再跑一次直径。
原理很简单,(1+(-1)=0) 。
时间复杂度:(O(n))
APIO2010T3 信号覆盖
题目即求:(frac{每种方案被圆覆盖(含边界)的点数}{C_n^3})
由于每种方案的三个点必定被覆盖,所以可以变成 (frac{每种方案在圆内的点数}{C_n^3}+3)
转换视角,分子即为无序四元组 ((i,j,k,t)) 满足 (t) 在 (i,j,k) 构成的圆内的对数。
题目保证三点不共线,四点不共圆,那么无非就两种情况:四个点形成凹四边形/凸四边形。
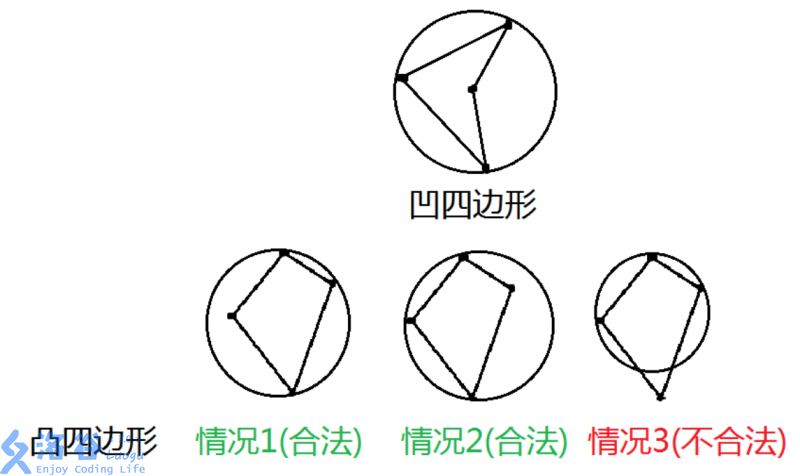
凹四边形的贡献为 (1) ,凸四边形的贡献为 (2) (凸多边形的其中一对角和 (>180°))
设凹四边形有 (k) 个,那么凸四边形有 (C_n^4-k) 个,答案为 (frac{k+2(C_n^4-k)}{C_n^3}+3)
瓶颈在于如何求出凹四边形数目,假设凹点为 (D) ,那么我们要找出三角形 (ABC) 包括 (D) 。
正难则反,考虑不包括 (D) 。
以 (D) 为坐标原点,所有点极角排序,然后用尺取法计算得到第 (i)个点最远到第 (j) 个点,使两向量夹角 (<180°) ,那么在 ((i,j)) 任意选一个 (k) 构成的三角形均不包括 (D) 。
数点完拿 ((C_{n-1}^3 - 答案)) ,即为所有包括 (D) 的三角形数了。
时间复杂度:(O(n^2logn))
APIO2012
APIO2012T1 派遣
枚举所有的领导者,在它子树内贪心挑薪水小的人,这样暴力是 (O(n^2)) 的。
用 左偏树 优化一下即可,挺裸的。
时间复杂度:(O(nlogn))
APIO2013
APIO2013T3 出题人
(1.in-6.in) 全是卡单源最短路,(7.in-8.in) 是神秘程序。
神秘问题:给一张图的每个节点染色,使得任何一条边两端点颜色不同,求最少用多少种不同的颜色
1: ModifiedDijkstra.cpp & FloydWarshall.cpp
卡掉 (Floyd) ,直接 (V=101) ,无边,(1) 组询问即可。
使用次数:(105,T=107)
2: FloydWarshall.cpp & OptimizedBellmanFord.cpp
卡掉 (BellmanFord) ,不卡 (Floyd) ,那么我们令 (V=100) ,这样 (Floyd) 不会超时。
然后,构造一些 (j) 到 (i) 边权依次增加 ((i<j)) 即可,让 (BellmanFord) 跑满 (V-1) 次。
使用次数:(2190,T=2222)
3: OptimizedBellmanFord.cpp & FloydWarshall.cpp
卡掉 (Floyd) ,不卡 (BellmanFord) ,那么我们令 (V=101) ,无边权,(1) 组询问即可。
使用次数:(105,T=105) ,卡的真紧...
4: FloydWarshall.cpp & ModifiedDijkstra.cpp
卡掉堆优化的(dijkstra) ,我们可以造负权图。
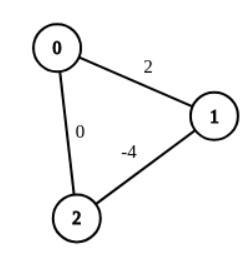
我们构造一连串负团(见上图),边权依次倍增,它复杂度就被卡成指数级了。
使用次数:(151,T=157)
5: ModifiedDijkstra.cpp & OptimizedBellmanFord.cpp
卡掉 (BellmanFord) ,不卡 (dijkstra) ,那简单了。
我想办法把 (BellmanFord) 的优化给抵消掉,那我建自环卡飞不就得了?
所以令 (V=300) ,然后 (0) 连向 (1) ,边权随意,然后对于 (ige 2) 建一个负自环,再随机加点边。
查询查 (10) 次 (0) 到 (1) 。
使用次数:(1016,T=1016)
6: OptimizedBellmanFord.cpp & ModifiedDijkstra.cpp
卡掉 (dijkstra) ,不卡 (BellmanFord) ,这和 #4 类似。
疯狂调参卡常即可。
使用次数:(143,T=143)
7: Gamble1.cpp & RecursiveBacktracking.cpp
这个Gamble1.cpp是恒过器,所以我们只需要使RecursiveBacktracking.cpp超时即可。
它是个爆搜,所以……我随便造一组大数据就把它卡飞??
使用次数:(3004,T=3004)
8: RecursiveBacktracking.cpp & Gamble2.cpp
这个Gamble2.cpp是恒挂器,所以我们只需要使RecursiveBacktracking.cpp跑的出来。
采用黑白染色,然后随便找黑点和白点连边即可,但 (i) 和 (i+1) 必须连。
使用次数:(3004,T=3004)
[汇总] 所有的数据生成器:代码
答案
APIO2019
预计得分:(100+100+80=280)
APIO2019T1 奇怪装置
数学题,求个线段交即可。
时间复杂度:(O(nlogn))
APIO2019T2 桥梁
将操作分块,然后用带撤销并查集维护一下即可。
设块长为 (S) ,则复杂度为 (O(Sqlog(n)+frac{qmlog(m)}{S}))
在 (S=sqrt{m}) 左右时复杂度最优,为 (O(qsqrt{m} logm))
UPD: 在洛谷上被硬生生卡常了,完美GG
其实可以再优化(其实是因为洛谷老爷机太慢),把排序用归并实现,块长为 (sqrt{frac{m}{log(n)}}),可达到 (O(qsqrt{mlogm}))
时间复杂度:(O(qsqrt{mlogm}))
APIO2019T3 路灯
假设 (i) 所能到达的最左和最右的位置为 (l_i) 和 (r_i) 。
考虑一个矩形 (M_{i,j}) 表示 (i) 可以出发到 (j) 的时刻数。
断开:
如果在 ([l,r]) 区间中,断了 ((x, x+1)) 这条路,区间变为 ([l,x]) 和 ([x+1,r])
那么在矩形中体现为:子矩形 ([(l,x+1),(x,r)]) 全体减 (q - 现在的时刻)
连接:
如果在 ([l,x],[x+1,r]) 区间中,连接了 ((x,x+1)) 这条路,区间合并为 ([l,r])
那么在矩形中体现为:子矩形 ([(l,x+1),(x,r)]) 全体加 (q - 现在的时刻)
这里的全体加/减本质为差分思想,连接/断开可以用 (set) 维护。
对于查询,本质上就是求前缀矩形 ([(1, 1), (a,b)]) 的和。
需要注意的是,如果当前 (a) 和 (b) 连通,则需要给计算的答案减去 (q - 现在的时刻)。
树套树即可,我用的是树状数组套动态开点线段树。
当然也可以离线跑 (CDQ) ,空间会省一点。
时间复杂度:(O(nlog^2n))