Dijkstra算法

　　Dijkstra算法用于求解单源最短路径问题。

　　Dijkstra算法最核心的步骤在于，每次从剩余节点中选取一个节点v加入已访问节点集合的时候，我们便以v为中间节点，查看从源点出发经过v到剩余节点k和不经过v到剩余节点k哪个更短，如果经过v到剩余节点k更短的话，我们需要更新从源点到k的距离值，以及将k的前驱设置为v。

　　换句话说就是，当我们从源点向目标节点走的时候，每走一步，下一步面临若干选择，当我们选择了目前的一条最短路，即选择了某个k点的时候，从源点到目标点的最短路就多了一种选择——走k和不走k。如果我们走k到剩余节点更短的话，我们当然要选择k，并且要更新这个最短路径。

　举个栗子

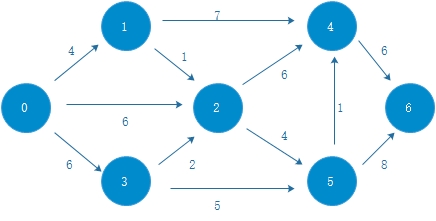
　　我们需要三个数组

dist数组，记录从源点到某点的最短路径长度
path数组，记录v点最短路径的上一个节点
visit数组，记录某点有没有被访问过

　（1）开始，我们站在源点，加入是0点，我们只能看到1、2、3，所以

	0	1	2	3	4	5	6
dist	inf	4	6	6	inf	inf	inf
path	-1	-1	-1	-1	-1	-1	-1
visit	1	-1	-1	-1	-1	-1	-1

　　开始时，我们选择了最小值1节点，此时剩余节点就是2、3、4、5、6。

　　以1为中间节点，更新到剩余顶点的值。

	0	1	2	3	4	5	6
dist	inf	4	5	6	11	inf	inf
path	-1	0	1	0	1	-1	-1
visit	1	1	0	0	0	0	0

　　这里解释一下，我们加入了1号节点，我们站在1，下一步我们能看到2和4，所以，2和4到源点的最短路可能因为经过1这条最新的路径而改变，例如，本来从源点到2的距离为6，由于经过1，源点到2的距离dist[1]+1=5<6，所以，源点到2的最短距离我们就要更新为5，且这个距离是通过走1这个节点得到的，所以，2的最短路径的前驱就更新为1。同理，0到4本来是无穷（因为站在0点，不知道怎么才能到4），但是，当我们站在1点，到4的距离为dist[1]+7=11，小于无穷，所以，我们更新源点到4的最短距离为11，到4的最短路径要经过1，所以4的前驱设置为1

（2）在当前的dist数组中选择最小的值2，下一步就是要以2为中间节点进行观察，也就是说，我们现在站在2处。此时剩余节点是3、4、5、6。

	0	1	2	3	4	5	6
dist	inf	4	5	6	11	9	inf
path	-1	0	1	0	1	2	-1
visit	1	1	1	0	0	0	0

　　同理，站在2处，我们能看到4和5，对于4，经过2到4距离为dist[2]+6=11，不更新。经过2到5,距离为dist[2]+4=9，小于无穷，更新之。

　　后面的操作就是进行重复，直到所有点的visit值为1。

　　最后我们得到的结果为

	0	1	2	3	4	5	6
dist	inf	4	5	6	10	9	16
path	-1	0	1	0	5	2	4
visit	1	1	1	1	1	1	1

　　最后dist数组就记录了从源点0到每个点的最短路径长度，path数组记录了最短路径上该点的上一个节点。

　　最后我们要输出最短路径，就是要不断利用path数组，借助栈进行输出。

　　例如，我们要输出从0到6的最短路径，6进栈，查path表，6的前面是4,4进栈，4的前面是5,5进栈，5的前面是2,2进栈，2的前面是1,1进栈，1的前面是0,0进栈，0的前面是-1，结束，所有元素出栈就是最短路径：0->1->2->5->6，最短路径长度为16。

  1 #include<cstdio>
  2 #define MAXSIZE 100
  3 #define INF 99999
  4 int MGraph[MAXSIZE][MAXSIZE];     //图
  5 int path[MAXSIZE];
  6 int dist[MAXSIZE];
  7 int visit[MAXSIZE];
  8 void init(int n)
  9 {
 10     for(int i = 0; i < n; ++i)
 11     {
 12         path[i]=-1;
 13         visit[i]=0;
 14     }
 15 }
 16 void createG(int e)
 17 {
 18     int val;
 19     int a,b;
 20     for(int i = 0; i < e; ++i)
 21     {
 22         for(int j = 0; j < e; ++j)
 23         {
 24             MGraph[i][j] = INF;
 25         }
 26     }
 27     for(int i = 0; i < e; ++i)
 28     {
 29         scanf("%d%d%d",&a,&b,&val);
 30         MGraph[a][b]=val;
 31     }
 32 }
 33 //获取当前从原点到剩余顶点最短路径坐标
 34 int getlowest(int n)
 35 {
 36     int mm=9999;
 37     int u;
 38     for(int i=0; i<n; ++i)
 39     {
 40         if(visit[i]==0&&dist[i]<mm)
 41         {
 42             u=i;
 43             mm=dist[i];
 44         }
 45     }
 46     return u;
 47 }
 48 void dijkstra(int v0,int n)
 49 {
 50     for(int i=0; i<n; ++i)
 51     {
 52         dist[i]=MGraph[v0][i];
 53         if(MGraph[v0][i]!=INF)
 54             path[i]=v0;
 55         else
 56             dist[i]=INF;
 57     }
 58     visit[v0]=1;
 59     for(int i=0;i<n;++i)
 60     {
 61         int u=getlowest(n);
 62         visit[u]=1;
 63         for(int j=0;j<n;++j)
 64         {
 65             if(visit[j]==0&&dist[u]+MGraph[u][j]<dist[j])
 66             {
 67                 dist[j]=dist[u]+MGraph[u][j];
 68                 path[j]=u;
 69             }
 70         }
 71     }
 72 }
 73 //利用栈打印最短路径，d为目标点
 74 void printPath(int n,int d)
 75 {
 76     int s[MAXSIZE];
 77     int top=0;
 78     int c=d;
 79     while(path[d]!=-1)
 80     {
 81         s[top]=path[d];
 82         d=path[d];
 83         ++top;
 84     }
 85     for(int i=top-1;i>=0;--i)
 86     {
 87         if(i!=0)
 88         printf("%d -> ",s[i]);
 89         else
 90             printf(" %d -> %d
",s[i],c);
 91     }
 92     printf("最短路径长度:%d",dist[c]);
 93 }
 94 int main()
 95 {
 96     int n,e;
 97     scanf("%d%d",&n,&e);
 98     init(n);
 99     createG(e);
100     int v0;
101     scanf("%d",&v0);
102     dijkstra(v0,n);
103     printPath(n,6);
104     return 0;
105 }

　　算法的时间复杂度为O（n²）。