基础概念
主成分分析(Principal Component Analysis,PCA), 是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
###原理: 在用统计分析方法研究多变量的课题时,变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有一定的相关关系的,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量,将重复的变量(关系紧密的变量)删去多余,建立尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映课题的信息方面尽可能保持原有的信息。
在pca中要用到的相关概念:
####协方差 协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。总的来说,协方差是一种用来度量两个随机变量关系的统计量。
协方差表示方式:

如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。如果X与Y是统计独立的,那么二者之间的协方差就是0。
换句话说,协方差为正时说明X和Y是正相关关系,协方差为负时X和Y是负相关关系,协方差为0时X和Y相互独立。
当样本是n维数据时,它们的协方差实际上是协方差矩阵(对称方阵),方阵的边长是C2n。比如对于3维数据(x,y,z),计算它的协方差就是:
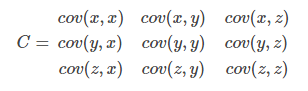
####pca计算过程
- 第一步,分别求特征的平均值,然后对于所有的样例,都减去对应的均值
- 第二步,求特征协方差矩阵
- 第三步,求协方差的特征值和特征向量
- 第四步,将特征值按照从大到小的顺序排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
- 第五步,将样本点投影到选取的特征向量上。假设样例数为m,特征数为n,减去均值后的样本矩阵为DataAdjust(mn),协方差矩阵是nn,选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为

整个过程,就是将原始样例的n维特征变成了k维,这k维就是原始特征在k维上的投影。
进行主成分分析主要步骤如下: 1. 指标数据标准化 2. 指标之间的相关性判定; 3. 确定主成分个数m; 4. 主成分Fi表达式; 5. 主成分Fi命名;
主成分分析(principal component analysis,PCA)是一种降维技术,把多个变量化为能够反映原始变量大部分信息的少数几个主成分。
设X有p个变量,为n*p阶矩阵,即n个样本的p维向量。首先对X的p个变量寻找正规化线性组合,使它的方差达到最大,这个新的变量称为第一主成分,抽取第一主成分后,第二主成分的抽取方法与第一主成分一样,依次类推,直到各主成分累积方差达到总方差的一定比例。
主成分分析实例
p=princomp(USArrests,cor=TRUE)
summary(p,loadings=TRUE)

----Standard deviation 标准差 其平方为方差=特征值
----Proportion of Variance 方差贡献率
----Cumulative Proportion 方差累计贡献率
screeplot(p,type="lines")

图中的点在第三个成分的下降已经变得非常平稳了,因而选择前两个变量就能获得较好的信息解释,这也就意味着后两个变量可以舍弃。
也可以利用loadings参数中反映的系数值对主成分进行构建方程
y=-0.536murder-0.583assault-0.278urbanpop-0.543rape
y=0.418murder+0.188assault-0.873urbanpop-0.167rape
pre<-predict(p)
pre

对个主成分的值进行预测的结果