如果需要小编其他数学基础博客，请移步小编的GitHub地址
传送门：请点击我
如果点击有误：https://github.com/LeBron-Jian/DeepLearningNote
这里我打算再补充一下关于常见概率分布，似然函数，后验概率估计和一些距离公式的基础。
（注意：目前自己补充到的所有知识点，均按照自己网课视频中老师课程知识点走的，同时一些公式是网友辛辛苦苦敲的，这里用到那个博客均在文末补充地址，不过这里首先表示感谢！！）
1，常见离散概率分布
介绍一个概念：PMF（概率质量函数）：是对离散随机变量的定义，是离散随机变量在各个特定取值的概率，该函数通俗来说，就是对于一个离散型概率事件来说，使用这个函数来求它的各个成功事件结果的概率。
1.1 0-1分布
0-1 分布是单个二值型（n=1情况下）离散随机变量的分布。即只先进行一次事件实验，该事件发生的概率为 p，不发生的概率为 1-p，这是一个最简单的分布，任何只有两种结果的随机现象都服从0-1分布，其概率分布函数为：
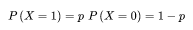性质：数学期望为 E(X) = p，方差为 D(X)=p(1-p)。
举个例子，比如抛硬币观察正反面，新生儿是男还是女，检测产品是否合格等，都可以用0-1分布描述。
1.2 伯努利分布
伯努利分布指的是对于随机变量 X 有参数为 p（0<p<1），如果它以概率 p 和 1-p 取 1和 0 的值。EX=p，DX=p(1-p)。伯努利试验成功的次数服从伯努利分布，参数p是试验成功的概率。伯努利分布是一个离散型机率分布，是 N=1时的二项分布的特殊情况，为纪念瑞士科学家詹姆斯*伯努利而命名。
如果随机变量 X 只取0和1两个值，并且相应的概率为：
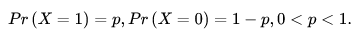
则称随机变量X服从参数为 p 的伯努利分布，若令 q = 1-p，则X的概率函数可写为：
1.3 二项分布（Binomial Distribution）
让我们看看玩板球这个例子，假设你今天赢了一场比赛，这表示一个成功的事件。你再比了一场，但是你输了。如果你今天赢了一场比赛，但这并不表示你明天肯定会赢。我们来分配一个随机变量X，用于表示赢得的次数。X可能的值是多少呢？他可以是任意值，这取决于你掷硬币的次数。只有两种可能的结果，成功和失败。因此，成功的概率为0.5，失败的概率也很容易计算出来，即 q = 1- p = 0.5。
二项分布即重复 n 次伯努利试验，各种试验之间都相互独立，并且每次试验中只有两种可能的结果，而且这两种结果发生与否相互对立，比如成功与失败，得到与失去等。如果每次试验时，事件发生的概率为 p，不发生的概率为 1-p，则 n次重复独立试验中发生 k 次的概率为：
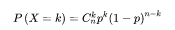
性质：每一次尝试都是独立的，因为前一次投掷的结果不能影响或决定当前投掷的结果。只有两个可能的结果并且重复n次的试验叫二项式，二项式分布的参数为n和p，其中n是试验总数，p是每次试验成功的概率，一般的二项分布是 n 次独立的伯努利试验的和，它的期望值和方差分别等于每次单独试验的期望值和方差的和：
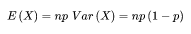
这个事实很容易证明。首先假设有一个伯努利试验。实验中有两个可能的结果：1和0，前者发生的概率为p，后者发生的概率为 1-p。该试验的期望值等于 1*p + 0*(1-p) = p。该试验的方差也可以类似的计算：σ2= (1−p)2·p+ (0−p)2·(1−p) =p(1 − p)
总结一下，二项式分布的属性包括：
- 1，每个实验都是独立的
- 2，在实验中只有两个可能的结果：成功或失败
- 3，总共进行了 n 次相同的实验
- 4，所有实验成功和失败的概率是相同的
1.4 泊松分布
Poisson分布，是一种统计与概率学里面常见到的离散概率分布，由法国数学家西摩恩*德尼*泊松在 2838年时发表，现实生活中多数服从泊松分布。
日常生活中，大量事件是由固定频率的，比如：
- 某医院平均每小时出生 3 个婴儿
- 某网站平均每分钟有 2次访问
- 某超市平均每小时销售 4 包奶粉
他们的特点就是，我们可以预估这些事情的总数，但是没法知道具体的发生时间。已知平均每小时出生 3 个婴儿，请问下一个小时，会出生几个？有可能一下出生 6 个，也有可能一个都不出生，这是我们没法知道的。
当以下假设有效时，则称为泊松分布：
- 1，任何一个成功的事件都不应该影响另一个成功的事件
- 2，在短时间内成功的概率必须等于在更长的时间内成功的概率
- 3，时间间隔很小时，在给间隔时间内成功的概率趋于零
泊松分布就是描述某段时间内，事件具体的发生概率。其概率函数为：
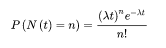
其中：P表示概率，N表示某种函数关系，t 表示时间（即时间间隔的长），n 表示数量（即该时间间隔内的事件数），λ 表示事件的频率，令 μ 表示长度为 t 的间隔中的平均事件数，那么 μ = λ*t。
例如说一个医院内，每个出生婴儿的都是随机并独立的概率，则该医院一天（或者其他特定时间段，一小时，一周等等）要出生的婴儿总数可以看作是一个服从 poisson 分布的随机变量。但是为什么可以这样处理你？通俗定义：假设一个事件在一段时间内随机发生，且符合以下条件：
- 1，将该时间段无限分割成果若干个小的时间段，在这个接近于零的小时间段内，该事件发生一次的概率与这个极小时间段的长度成正比
- 2，在每个极小时间段内，该事件发生两次及以上的概率恒等于零
- 3，该事件在不同的小时间段里，发生与否相互独立
继续用上面的例子，1小时内出生3个婴儿的概率，就表示为 P(N(1) = 3)，那么接下来两个小时，请问会出生几个孩子？
有可能一下生出6个孩子，也有可能一个都不出生，这是我们没法知道的。而泊松分布就是描述某段时间内，事件具体发生的概率。
一个婴儿都不出生的概率可以求得为0.0025，说明概率非常小，基本不可能发生，计算如下：
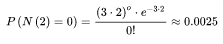
同理，我们可以求接下来一个小时，至少出生两个婴儿的概率0.8，说明概率非常大，计算如下：
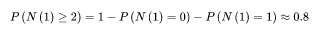
完整计算如下：
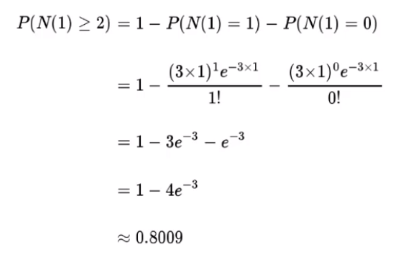
泊松分布的图形大概是下面的样子：
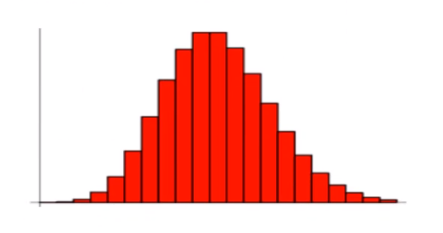
1.5 泊松分布与二项分布的关系
当二项分布的 n 很大而 p 很小时，泊松分布可作为二项分布的近似，其中 λ 为 np。通常当 n >=20，p <=0.05时，就可以用泊松公式近似的计算。
事实上，泊松分布正是由二项分布推导而来的。
2，常见连续概率分布
与PMF相对应的，在连续随机变量中叫 PDF（概率密度函数）：是对连续性随机变量的定义，与PMF 不同的是 PDF 在特定点上的值并不是该点的概率，连续随机概率事件只能求一段区域内发生事件的概率，通过对这段区间进行积分来求，通俗来说，使用这个概率密度函数将想要求的概率的区间的临界点（最大值和最小值）带入求积分，就是该区间的概率。
2.1 均匀分布
在概率论和统计学中，均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。均匀分布由两个参数a和b定义，他们是数轴上的最小值和最大值，通常缩写为 U(a, b)
对于掷骰子来说，结果是1~6，得到任何一个结果的概率是相同的，这就是均匀分布的基础。与伯努利分布不同，均匀分布的所有可能结果的 n 个数也是相等的。如果变量 X 是均匀分布的，则密度函数可以表示为：
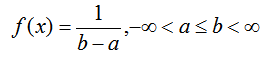
均匀分布的曲线是这样的：
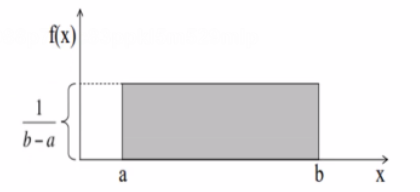
你可以看到，均匀分布曲线的形状是一个矩形，这也是均匀分布又称为矩形分布的原因，其中a和b是参数。
均值和方差如下：
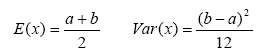
举个例子，花店每天销售的花束数量是均匀分布的，最多为 40 ，最小为 10，我们来计算一下销售量在 15~30之间的概率。
日销售量 在 15~30之间的概率为 （30-15）/（40-10）） = 0.5，同样的，日销售量大于 20 的概率为 0.667。
2.2 指数分布
在概率理论和统计学中，指数分布（也称为负指数分布）是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。这是伽马分布的一个特殊情况。他是几何分布的连续模拟，它具有无记忆的关键性质。除了用于分析泊松过程外，还可以在其他各种环境中找到。
指数分布是指事件的时间间隔的概率，它的一个重要特征是无记忆性。例如：如果某一元件的寿命为T，已知元件使用了 t 小时，它总共使用至少 t+s 小时的条件概率，与从开始使用时他使用至少 s 小时的概率相等。下面这些都属于指数分布：
- 婴儿出生的时间间隔
- 网站访问的时间间隔
- 奶粉销售的时间间隔
指数分布的公式可以从泊松分布推断出来。如果下一个婴儿要间隔时间 t，就等同于 t 之内没有任何婴儿出生，即：
则：
如：接下来 15 分钟，会有婴儿出生的概率为：
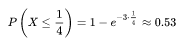指数分布的图像如下：
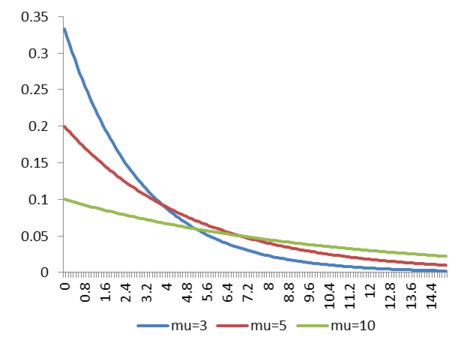
指数分布的均值和方差：
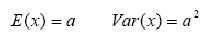
2.3 高斯分布（整体分布）
高斯分布又叫正态分布，其曲线呈钟形，两头低，中间高，左右对称因其曲线呈钟形，如下图所示：
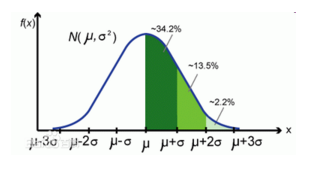若随机变量 X 服从一个数学期望为 μ ，方差为 σ2 的概率分布，且其概率密度函数为：
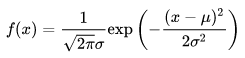
则这个随机变量就称为正态随机变量，正态随机变量服从的分布称为正态分布，我们将其记为：X~N(μ， σ2)。其期望值 μ 决定了正态分布的位置，其标准差 σ （方差的开方）决定了正态分布的幅度。
标准正态分布为当 μ = 0， σ = 1时，正态分布就成了标注正态分布：
正态分布为什么常见？
真正原因是中心极限定理（Central limit theorem）。根据中心极限定理，如果一个事物受到多种因素的英雄，不管每个匀速本身是什么分布，他们加总后，结果的平均值就是正态分布。正态分布只适合各种因素累加的情况，如果这些因素不是彼此独立的，会互相加强英雄，那么就不是正态分布了。
2.4 卡方分布（Chi-Squared Distribution)
卡方分布通俗的说，就是通过小数量的样本容量去预估总体容量的分布情况。卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度。
若 n 个相互独立的随机变量 ζ1， ζ2， ζ3.... ζn，均服从标准正态分布（也称独立同分布于标准正态分布），则这 n 个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律成为卡方分布（chi-square distribution)。
自由度：假设你现在手头有3个样本。因为样本具有随机性，所以他们取值不定。但是假设处于某种原因，我们需要让样本均值固定，比如说有一个样本是固定的，那么这时真正取值自由，”有随机性“ 的样本只有两个，试想，如果每取一组的值，将影响下一组的值，那么对于后面样本来说，就被剥夺了自由度。所以就这个例子而言，三个样本最终”自由“的样本只有一个。
卡方检验的思想是根据样本数据推断总体的频次与期望频次是否有显著性差异。
公式如下：
2.5 beta 分布
贝塔分布（Beta Distribution） 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数，在及其学习和数理统计学中有重要应用。在概率论中，贝塔分布也称为 B分布，是指一组定义在（0， 1）区间的连续概率分布。
B 分布的概率密度函数为：
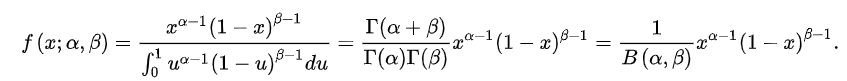
其中，Γ(z) 是 Γ 函数，随机变量 X 服从参数为 α，β 的 B 分布通常写作：
B 分布的累积分布函数是：
其中 Bx(α，β ) 是不完全 B 函数， Ix(α，β ) 是正则不完全贝塔函数。
简单说，Beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，他可以给出来所有概率出现的可能性大小。
举一个简单的例子，熟悉棒球运动的都知道有一个指标就是棒球击球率（ betting average)，就是用一个运动员击中的球数除以击球的总数，我们一般认为 0.266 是正常水平的击球率，而如果击球率高达 0.3 就被认为是非常优秀的。现在有一个棒球运动员，我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率，用击中的数除以击球数，但是如果这个棒球运动员只打了一次，而且还命中了，那么他的击球率就是 100%，这显然是不合理的，因为根据棒球的历史信息，我们知道这个击球率应该是 0.215~0.36之间才对。所以对于这个问题一个最好的办法就是用 beta 分布，这表示我们没有看见这个运动员打球之前，我们就有了一个大概的范围。beta分布的定义域是（0， 1），这就跟概率的范围是一样的。接下来我们将这些先验信息转换为 beta 分布的参数，我们知道一个击球率应该是平均 0.27 左右，而他的范围是 0.21~0.35 ，那么根据这个信息，我们可以取 α = 81，β = 219 （击中了 81 次，未击中 219 次）。
之所以取这两个参数是因为：
- beta 分布的均值是从图中可以看到这个分布主要落在了 （0.2， 0.35）区间，这是从经验中得到的合理范围
- 在这个例子中，我们的 x 轴就表示各个击球率的取值，x 对应的 y 值就是这个击球率所对应的概率，也就是说 beta 分布可以堪称一个概率的概率分布
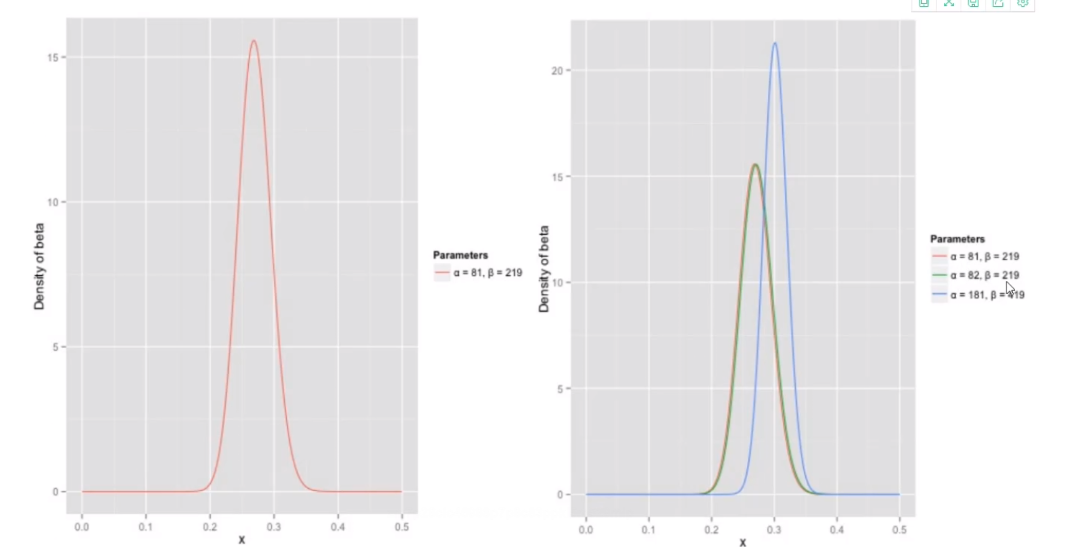
0 和 β0 是一开始的参数，在这里是 81 和 219，当 α 增加了 1（击中了一次）。β 没有增加（没有漏球）。这就是我们的新的 beta 分布 Beta(81, 219)，可以看到这个分布其实没有多大的变化，这是因为只打了一次球并不能说明什么问题。但如果我们得到了更多的数据，假设一共打了 300 次，其中击中了 100次，200次没有击中，那么这一新分布就是 Beta（81+100， 219+200）。注意到这个曲线变得更尖，并且平移到了一个右边的位置，表示比平均水平要高。因此，对于一个我们不知道概率是什么，而又有一些合理的猜测时，Beta分布能够很好的作为一个表示概率的概率分布。
3， 极大似然估计与最大后验概率估计
3.1 概率和似然的区别
其实将似然放在这里有些不妥，毕竟似然和概率还是有些区别的。不过我在学习似然之前，还是先学习一下其与概率的区别。
概率用于在已知一些参数的情况下，预测接下来的观测所得到的结果，而似然性则是用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。这里需要对参数估计进行说明，参数估计（parameter estimation） 则是根据从总体中抽取的样本估计总体分布中包含的未知参数的方法。人们常常需要根据手中的数据，分析或推断数据反应的本质规律。即根据样本数据如何选择统计量去推断总体的分布或数字特征等。统计推断是数理统计研究的核心问题。所谓统计推断是根据样本对总体分布或分布的数字特征等做出合理的推断。他是统计推断的一种基本形式，是数理统计学的一个重要分支，分为点估计和区间估计两部分。
顺带提一下先验概率和后验概率的区别：
先验概率是指根据以往经验和分析得到的概率，如全概率公式中的，他往往作为”由因求果“问题中的”因“ 出现。后验概率是指在得到”结果“ 的信息后重新修正概率，是”执果寻因“ 问题中的”因“。
3.2 频率学派和贝叶斯学派
在说极大似然估计（Maximum Likelihood Estimate） 与最大后验概率估计（Maximum A Posteriori estimation）之前，我们要学习一下对概率看法的两大学派频率学派和贝叶斯学派。他们看待世界的视角不同，导致他们对于产生数据的模型参数的理解也不同。
频率学派
他们认为世界是确定的。他们直接为事件本身建模，也就是说事件在多次重复实验中趋于一个稳定的值 p，那么这个值就是该事件的概率。
他们认为模型参数是个定值。希望通过类似解方程组的方式从数据中求得未知数。这就是频率学派使用的参数估计方法——极大似然估计（MLE），这种方法往往在大数据量的情况下可以很好的还原模型的真实情况。
贝叶斯学派
他们认为世界是不确定的，因获取的信息不同而异。假设对世界先有一个预先的估计，然后通过获取的信息来不断调整之前的预估计。他们不试图对事件本身进行建模，而是从旁观者的角度来说。因此对于同一个事件，不同的人掌握的先验不同的话，那么他们所认为的事件状态也会不同。
他们认为模型参数源自于某种潜在的分布，希望从数据中推出该分部。对于数据的观测方式不同或者假设不同，那么推知的该参数因此也存在差异。这就是贝叶斯学派视角下用来估计参数的常用方法——最大后验概率估计（MAP），这种方法在先验假设比较靠谱的情况下效果显著，随着数据量的增加，先验假设对于模型参数的主导作用会逐渐削弱，相反真实数据样例会大大占据有利地位。极端情况下，比如把先验假设去掉，或者假设先验满足均匀分布的话，那么她和极大似然估计就如出一辙。
3.3 似然函数的概念
统计学中，似然函数是一种关于统计模型参数的函数，表示模型参数中的似然性。给定输出 x 时，关于参数 Θ 的似然函数 L(Θ|x) （在数值上）等于给定参数 Θ 后变量 X 的概率：
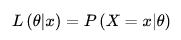
其中 P(x|Θ) 是密度函数，表示给定 Θ 下的联合密度函数。而似然函数是关于 Θ 的函数，密度函数是关于 x 的函数。
似然函数在推断统计学（Statistical inference）中扮演重要角色，如在最大似然估计和费雪信息之中的应用等等。“似然性” 与 “或然性” 或“概率” 意思相近，都是指某件事情发生的可能性，但是在统计学中，“似然性” 与 “或然性” 或“概率” 又有明确的区分。概率用于在已知一些参数的情况下，预测接下来的观测所得到的结果，而似然性则是用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。
离散型概率分布：假设一个关于参数 Θ ，具有离散型概率分布 P 的随机变量 X，则在给定 X 的输出X时，参数 Θ 的似然函数可表示为：
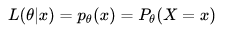
其中， p(x) 表示 X 取 x 时的概率。上式常常写为 P(X=x|Θ) 或者 P(X=x ;Θ)，需要注意的是，此处并非条件概率，因为 Θ 不（总）是随机变量。
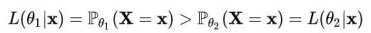
如果有上式成立，则在参数 Θ1 下随机变量 X取到 x 值的可能性大于 Θ2。
连续型概率分布：假定一个关于参数 Θ，具有连续概率密度函数 f 的随机变量X，则在给定 X 的输出 x 时，参数 Θ 的似然函数可表示为：
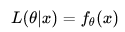
上式常常写为 f(x|Θ)，同样需要注意的是，此处并非条件概率密度函数。
连续情况下的概率密度函数是：如果X是连续随机变量给定足够小的 ε >0 ，那么其在（x-ε, x+ε）内的概率为：
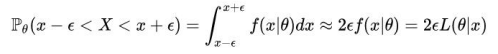
得到的结果与离散型是一致的，概率表达了在给定参数 Θ 时X=x 的可能性而似然表示的是给定样本 X=x 时，参数的可能性！
3.4 极大似然估计
极大似然估计方法（Maximum Likelihood Estimate，MLE）也称为最大概似估计或最大似然估计，它是频率学派模型参数估计的常用方法，是求估计的另一种方法。
似然，可以简单理解为概率，可能性。极大似然估计，通俗理解就是：利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！换句话说：极大似然估计提供了一种给定观察数据来评估模型参数的方法，即“模型已定，参数未知”。
极大似然估计的原理：它是建立在极大似然原理的基础上的一个统计方法，极大似然原理的直观想法是，一个随机试验如有若干个可能的结果A，B，C，...，若在一次实验中，结果A出现了，那么可以认为实验条件对A的出现有利，也即出现的概率P(A) 较大。极大似然原理的直观想法我们用心下面的例子说明。设甲箱中有 99 个白球，1个黑球；乙箱中有1个白球，99个黑球。现随机取出一箱，再从抽取的箱子中随机取出一球，结果是黑球，这一黑球从乙箱抽取的概率比甲箱抽取的概率大得多，这时我们自然更多的相信这个黑球是取自乙箱的。一般来说，事件A发生的概率与某一未知参数 Θ 有关，Θ 取值不同，则事件发生的概率 P(A|Θ) 也不同，当我们在一次实验中事件A发生了，则认为此时的 Θ 值应该是 t 的一切可能取值中使 P(A|Θ) 达到最大的哪一个，极大似然估计法就是要选取这样的 t 值作为参数 t 的估计值，使所选取的样本在被选的总体中出现的可能性为最大。
或者看如下例子：
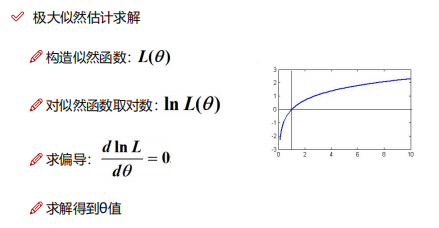
求极大似然函数估计值的一般步骤：
- 1，写出似然函数
- 2，对似然函数取对数，并整理
- 3，求导数
- 4，解似然函数
利用高等数学中求多元函数的极值的方法，有以下极大似然估计法的具体做法：
1，根据总体的分布，建立似然函数 L(x1, x2,...xn；Θ1,Θ2,...Θk)
2，当 L关于 Θ1,Θ2,...Θk 可微时，（由微积分求极值的原理）可知方程组：
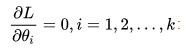
定出 Θhati(i=1,2,...k)，称以上方程组为似然函数。
因为 L与 InL 具有相同的极大值点，所以 Θhati(i=1,2,...k) 也可由方程组
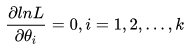定出 Θhati(i=1,2,...k) ，称以上方程组为对数似然方程；Θhati(i=1,2,...k) 就是所求参数Θi(i=1,2,...k) 的极大似然估计值。
当总体是离散型的，将上面的概率密度函数 f(x, Θ1,Θ2,...Θk) 换成它的分布律：
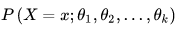
例1：设X服从参数 λ（ λ > 0） 的泊松分布， x1, x2,...xn 是来自 X 的一个样本值，求 λ 的极大似然估计值。
因为 X的分布律为：
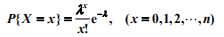
所以 λ 的似然函数为：
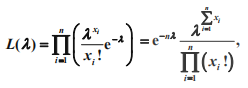
对似然函数取对数：
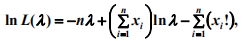
再取 λ 的偏导数等于 0的解：
解得 λ 的极大似然估计值为：
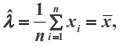
例2：假设一个盒子里面有红黑共10个球，每次有放回的取出，取了10次，结果为7次黑球，3次红球。问拿出黑球的概率 p 是多少？
我们假设7次黑球，三次红球为事件 A，一个理所当然的想法就是既然事件 A 已经发生了，那么事件 A 发生的概率应该最大。所以既然事件 A 的结果已定，我们就有理由相信这不是一个偶然发生的事件，这个已发生的事件肯定一定程度上反映了黑球在整体中的比例。所以我们要让模型产生这个整体事件的概率最大，我们把这十次抽取看成一个整体事件 A，很明显事件 A发生的概率是每次子事件概率之积。我们把 P(A) 看成一个关于 p 的函数，求 P(A) 取最大值时的 p，这就是极大似然估计的思想。具体公式化描述为 P(A) = p7*(1-p)3，接下来就是取对数转换为累加，然后通过求导令式子为 0 来求极值，求出 p 的结果。
3.5 最大后验概率估计
最大后验概率估计（Maximum a posteriori probability estimate，简称 MAP）是贝叶斯模型参数估计的常用方法，与最大似然估计类似，但是在似然函数后面多乘了一项，即“待估计参数的先验分布”。故最大后验估计可以看做规则化的最大似然估计。
顾名思义就是最大化在给定数据样本的情况下模型参数的后验概率。它依然是根据已知样本，来通过调整模型参数使得模型能够产生该数据样本的概率最大，只不过对于模型参数有了一个先验假设，即模型参数可能满足某种分布，不再一味地依赖数据样例（万一数据量少或者数据不靠谱呢）。
根据贝叶斯理论，对于 θ 的后验分布：
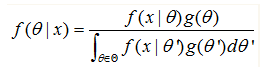
后验分布的目标为：
分母为 f(x) ，是固定值。
MAP 认为， θ 是一个随机变量，其先验概率密度函数是已知的，为 P(θ)，所以其目标为：
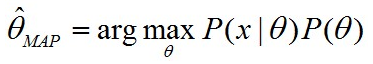
MLE 认为，θ 是非随机变量或者分布未知的随机变量，这两种情况都可以认为 P(θ) 均匀分布的，即该概率是一个固定值，P(θ)=C，所以其目标为：
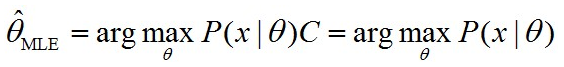
注意：最大后验估计可以看做是贝叶斯估计的一种特定形式。
在这里举个掷硬币的例子：掷一枚硬币10次，有10次正面朝上，0次反面朝上。问证明朝上的概率 θ。
在频率学派看来，利用极大似然估计可以得到 θ = 10/10 = 1.0 。显然当缺乏数据时 级大师让邮寄会产生严重的偏差。
如果我们利用最大后验概率估计来看这件事，先验认为大概率下这个硬币是均匀的（例如最大值取在0.5 处的 beta分布），那么P(θ|X) 是一个分布，最大值会介于 0.5~1 之间，而不是武断的给出 θ =1。
显然，随着数据量的增加，参数分布会更倾向于向数据靠拢，先验假设的影响会越来越小。
3.6 经验风险最小化与结构风险最小化
经验风险最小化与结构风险最小化是对于损失函数而言的。可以说经验风险最小化只侧重训练数据集上的损失降到最低；而结构风险最小化是在经验风险最小化的基础上约束模型的复杂度，使其在训练数据集的损失降到最低的同时，模型不至于过于复杂，相当于在损失函数上增加了正则项，防止模型出现过拟合状态。这一点也符合了奥卡姆剃刀原理：如无必要，勿增实体。
经验风险最小化可以看做是采用了极大似然估计的参数评估方法，更侧重从数据中学习模型的潜在参数，而且是只看重数据样本本身。这种在数据样本缺失的情况下，很容易管中窥豹，模型发生过拟合的状态；结构风险最小化采用了最大后验概率估计的思想来推测模型参数，不仅仅是依赖数据，还依靠模型参数的先验假设。这样在数据样本不是很充分的情况下，我们可以通过模型参数的先验假设，辅助以数据样本，做到尽可能的还原真实模型分布。
经验风险最小化
MLE（极大似然估计）是经验风险最小化的例子。当模型是条件概率分布，损失函数是对数损失函数时，经验风险最小化就等价于极大似然估计。这里举个逻辑（LR）回归的例子。
- 对于二分类的逻辑回归来说，我们试图把所有数据正确分类，要么0，要么1
- 通过累乘每个数据样例来模拟模型产生数据的过程，并最大化 ΠP(1)ΠP(0)
- 我们需要通过取对数来实现概率之积转为概率之和 Σ lnP(1) + Σ lnP(0)
- 我们可以根据数据标签的0， 1 特性来将上式改为 1/m*Σ(y * lnP(1) + (1-y) * lnP(0) )
这样我们通过极大似然估计来推导出了逻辑回归的损失函数，同时极大似然是经验风险最小化的一个特例。
结构风险最小化
MAP（最大后验概率估计）是结构风险最小化的例子。当模型是条件概率分布，损失函数是对数损失函数，模型复杂度由模型的先验概率表示时，结构风险最小化就等价于最大后验概率估计。在这里举个推荐系统中的矩阵概率分解（PMF）的例子。
- 先说一下矩阵分解的原理：推荐系统的评分预测场景可以看做是一个矩阵补全的游戏，矩阵补全是推荐系统的任务，矩阵分解是其达到目的的手段。因此，矩阵分解是为了更好地完成矩阵补全任务（欲其补全，先其分解之）。之所以可以利用矩阵分解来完成矩阵补全的操作，那是因为基于这样的假设——假设 UI矩阵是低秩的，即在大千世界中，总会存在相似的人或物，即物以类聚人以群分，然后我们可以利用两个小矩阵相乘来还原评分大矩阵。
- 它假设评分矩阵中的元素 Rij 是由用户潜在偏好向量 Ui 和物品潜在属性向量 Vj 的内积决定的，并且服从均值为 UiTVj ，方差为 σ2 的正态分布：Rij~n(UiTVj, σ2)
- 则观测到的评分矩阵条件概率为：
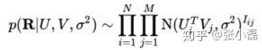同时，假设用户偏好向量与物品偏好向量服从均值都为0，方差分别为 σ2 UI, σ2VI 的正态分布：
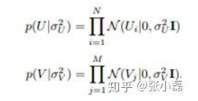
- 根据最大后验概率估计，可以得出隐变量 U，V 的后验概率为：
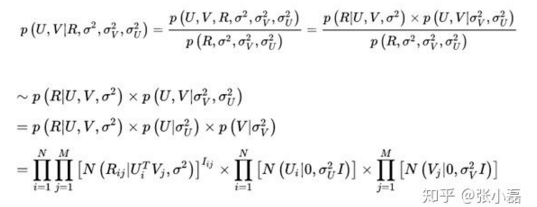
- 接着，等式两边取对数 In，并且将正态分布展开后得到：
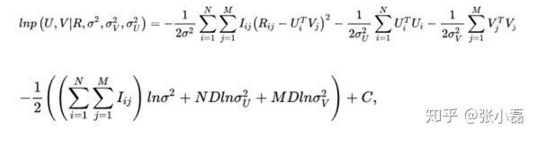
这样，我们通过最大后验概率估计推导出了概率矩阵分解的损失函数。可以看出结构风险最小化是在经验风险最小化的基础上增加了模型参数的先验。
3.7 MLE 和 MAP 的联系
在介绍经验风险与结构风险最小化的时候以具体的逻辑回归（LR）与概率矩阵分解（PMF）模型来介绍 MLE 和 MAP，接下来从宏观的角度，不局限于具体的某个模型来推导 MLE 和 MAP。
假设数据 x1, x2, ....xn 是满足独立同分布（i.i.d）的一组抽样 X=(x1, x2, ...xn)，接下来就利用两种参数估计方法来求解。
- MLE 对参数 θ 的估计方法如下：
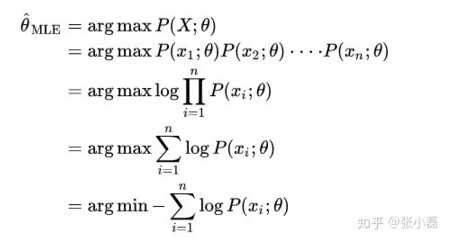
- MAP 对参数 θ 的估计方法如下：
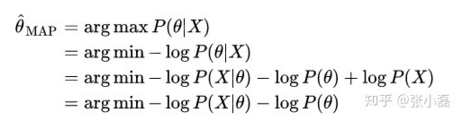
所以 MAP 和 MLE 在优化时的不同就是在于增加一个先验项 -log P(Θ)。
通过上面的分析可以大致给出他们的联系：MAP(Θ) ≈ MLEP(Θ) -log P(Θ)
4，几种常用的距离
在机器学习里，我们的运算一般都是基于向量的，一条用户具有100个特征，那么它对应的就是一个 100 维的向量，通过计算两个用户对应向量之间的距离值大小，有时候能反映出这两个用户的相似程度（这个在KNN算法和K-Means算法中很明显）。
这里设有两个 n 维变量 A={x11, x12, ... x1n} 和 B={x21, x22, ... x2n}，则一些常用的距离公式定义如下：
4.1 曼哈顿距离
曼哈顿距离也称为城市街区距离，数学定义如下：
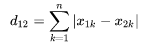
曼哈顿距离的 Python实现：
from numpy import * vector1 = mat([1,2,3]) vector2 = mat([4,5,6]) Manhattan_distance = sum(abs(vector1 - vector2))
4.2 欧式距离
欧式距离其实就是L2范数，数学定义如下：
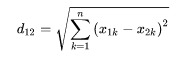
欧式距离的Python实现：
from numpy import * vector1 = mat([1,2,3]) vector2 = mat([4,5,6]) Euclidean_distance = sqrt((vector1 - vector2)*(vector1 - vector2).T)
4.3 闵可夫斯基距离
从严格意义上讲，闵可夫斯基距离不是一组距离，而是一组距离的定义：
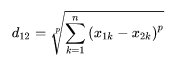
实际上，当 p=1 时，就是曼哈顿距离；当 p=2 时，就是欧式距离。
4.4 切比雪夫距离
切比雪夫距离就是 Lw，即无穷范围，数学表达式如下：
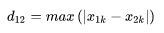
切比雪夫距离Python实现如下：
from numpy import * vector1 = mat([1,2,3]) vector2 = mat([4,5,6]) Chebyshev_distance = sqrt(abs(vector1 - vector2).max)
4.5 夹角余弦
夹角余弦的取值范围为 [-1, 1]，可以用来衡量两个向量方向的差异；夹角余弦越大，表示两个向量的夹角越小；当两个向量的方向重合时，夹角余弦取最大值1，当两个向量的方向完全相反时，夹角余弦取最小值 -1。
机器学习中用这一概念来衡量样本向量之间的差异，其数学表达式如下：
夹角余弦的Python实现如下：
from numpy import * vector1 = mat([1,2,3]) vector2 = mat([4,5,6]) IncludedAngleCosine = dot(vector1,vector2)/(linalg.norm(vector1)*linalg.norm(vector2))
4.6 汉明距离
汉明距离定义的是两个字符串中不相同维数的数目。例如：字符串“1111”与“1001”之间的汉明距离为2。
信息编码中一般应使得编码间的汉明距离尽可能的小。
汉明距离的Python实现：
from numpy import * matV = mat([1,1,1,1], [1,0,0,1]) Hanming_distance = nonzero(matV[0] - matV[1])
4.7 杰拉德相似系数
两个集合 A 和 B 的交集元素在 A 和 B 的并集中所占的比例称为两个集合的杰拉德相似系数，用符号 J(A, B) 表示，数学表达式为：
杰拉德相似系数是衡量两个集合的相似度的一种指标。一般可将其用在衡量样本的相似度上。
4.8 杰拉德距离
与杰拉德相似系数相反的概念是杰拉德距离，其定义式为：
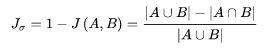杰拉德距离的Python实现：
from numpy import * import scipy.spatial.distance as dist matV = mat([1,1,1,1],[1,0,0,1]) jaccard_distance = dist.pdist(matV,'jaccard')
参考地址： 距离 https://zhuanlan.zhihu.com/p/25197792
https://zhuanlan.zhihu.com/p/40024110