浅析二分图最大匹配

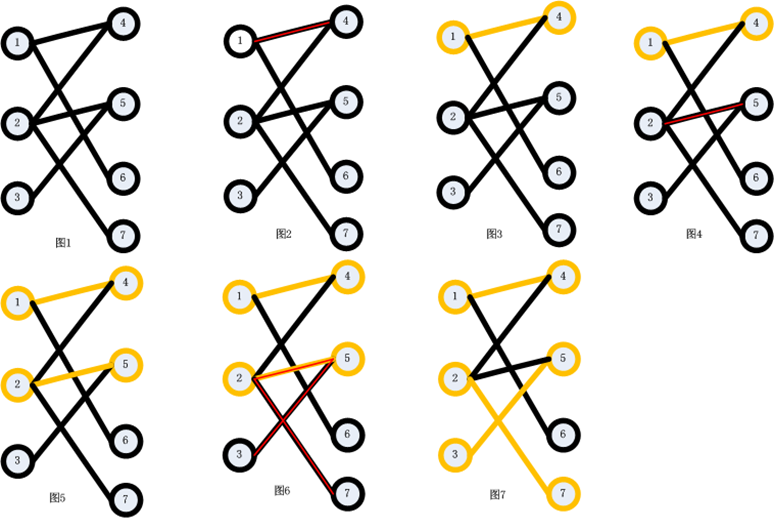
二分图：简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图，如图2所示

匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配

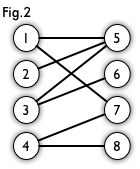
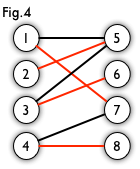
我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

基本概念讲完了。求解最大匹配问题的一个算法是匈牙利算法，下面讲的概念都为这个算法服务。

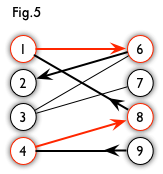
交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。

增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：

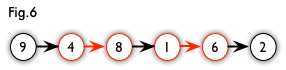
增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。

我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的，一般来说可以用$DFS/BFS$实现

下面对$DFS$稍做说明：

因为增广路长度为奇数，路径起始点非左即右，所以我们先考虑从左边的未匹配点找增广路。注意到因为交错路的关系，增广路上的第奇数条边都是非匹配边，第偶数条边都是匹配边，于是左到右都是非匹配边，右到左都是匹配边。于是我们给二分图定向，问题转换成，有向图中从给定起点找一条简单路径走到某个未匹配点，此问题等价给定起始点$s$能否走到终点$t$。那么只要从起始点开始 $DFS$ 遍历直到找到某个未匹配点，$O(m)$。枚举$n$个点，复杂度为$O(n*m)$

对于所有增广路径来说，它的长度为奇数，起点和终点必然分别在两个集合中，可以规定所有起点都在左集合中，则当左集合的点增广路寻找完后，整个算法就结束了。因此我们建图的时候只用建立左集合到右集合的单向边即可，标记匹配边的时候也只用标记右到左的边。

可以结合下面的过程图理解下:

#include<iostream>
using namespace std;
const int maxn = 2e5+100;
int n, m, k, ans;
int head[1010], tot;
int vis[2020], match[1010], u, v, dfn;
struct node{
    int to, nxt;
}e[maxn<<1];
void add(int u, int v){
    e[++tot].to = v;
    e[tot].nxt = head[u];
    head[u] = tot;
}
bool dfs(int u){
    for(int i = head[u]; i ; i = e[i].nxt){
        int v = e[i].to;
        if(vis[v]!=dfn){ //这一轮还没有遍历到
            vis[v] = dfn;
            if(!match[v]||dfs(match[v])){ //找到了一条增广路径
                match[v] = u;//匹配边v->u 
                return true;
            }
        }
              
    }
    return false;
}
int main(){
    cin >> n >> m >> k;
    for(int i = 1; i <= k; i++){
        cin >> u >> v;
        add(u, v);
    }
    for(int i = 1; i <= n; i++){
        dfn++;//小技巧，用于每轮寻找增广路，标记是否被访问过 
        if(dfs(i)) ans++;//找到了一条增广路
    }    
    cout << ans << endl;
}

View Code

Reference:

https://oi-wiki.org/graph/bi-graph/

https://oi-wiki.org/topic/graph-matching/bigraph-match/

https://www.renfei.org/blog/bipartite-matching.html

https://www.cnblogs.com/czsharecode/p/9777533.html

https://www.cnblogs.com/penseur/archive/2013/06/16/3138981.html

https://www.cnblogs.com/jianglangcaijin/p/6035950.html

https://www.luogu.com.cn/blog/Repulser/solution-p3386

https://www.luogu.com.cn/blog/OnePunchManGO/solution-p3386