前言
树链剖分,我觉得最精妙的地方就在于它是通过$dfs$序将树形结构转为线性结构便于处理,进而可以用数据结构(线段树、树状数组等)去进行修改和查询。
将复杂的结构转化为相对我们熟悉简单的结构,这个思想对很多问题是通吃的,不仅仅在树形问题,算法中,在其他领域中也常常会用到这种思想
我们先来回顾两个问题:
1.将树从$x$到$y$结点最短路径上所有节点的值都加上z
我们很容易想到,树上差分可以以 $O(n+m)$的优秀复杂度解决这个问题
2.求树从$x$到$y$结点最短路径上所有节点的值之和
$lca$大水题,我们又很容易地想到, $dfs$ $O(n)$预处理每个节点的$dis$(即到根节点的最短路径长度)
然后对于每个询问,求出$x,y$两点的$lca$,利用$lca$的性质$dis(x,y)=dis(x)+dis(y)-2*dis(lca)$求出结果,时间复杂度 $O(mlogn+n)$
现在来思考一个$bug$:
如果刚才的两个问题结合起来,成为一道题的两种操作呢?
刚才的方法显然就不够优秀了(每次询问之前要跑$dfs$更新 $dis$ )
理解
树剖是通过轻重边剖分将树分割成多条链,然后利用数据结构来维护这些链(本质上是一种优化暴力)
给定一棵有根树,对于每个非叶结点$u$,设$u$的子树中结点数最多的子树的树根为$v$,则标记$(u,v)$为重边,从$u$出发往下的其他边均为轻边
如图所示(结点中的数字代表结点的$size$值,即以该结点为根的子树的结点数)
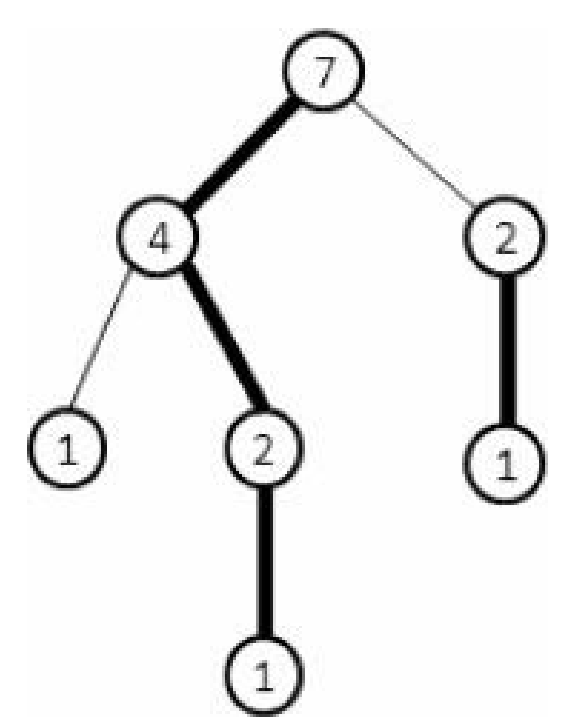
根据上面的定义,只需一次$DFS$就能把一棵有根树分解成若干重路径(重边组成的路径)和若干轻边。
有些资料也把重路径称为树链,因此轻重路径剖分也称树链剖分。 (下面的定理结论可不看)
路径剖分中最重要的定理如下:若$v$是$u$的子结点,$(u,v)$是轻边,则$size(v)<size(u)/2$,其中$size(u)$表示以$u$为根的子树中的结点总数(可以自己推导下)
由此可以得到如下的重要结论:对于任意非根结点$u$,在$u$到根的路径上,轻边和重路径的条数均不超过$log_{2}n$,因为每碰到一条轻边,$size$值就会减半。(对于概念,我还是觉得刘汝佳讲的最准确和便于理解)
因此重链剖分可以将树上的任意一条路径划分成不超过$O(logn)$条连续的链,每条链上的点深度互不相同(即是自底向上的一条链,链上所有点的 $LCA$ 为链的一个端点)。
重链剖分还能保证划分出的每条链上的节点 $DFS$ 序连续,因此可以方便地用一些维护序列的数据结构(如线段树)来维护树上路径的信息,如:
1.修改 树上两点之间的路径上 所有点的值
2.查询 树上两点之间的路径上 节点权值的 和/极值/其它(在序列上可以用数据结构维护,便于合并的信息)
除了配合数据结构来维护树上路径信息,树剖还可以用来$O(logn)$ (且常数较小)地求 $LCA$。
在某些题目中,还可以利用其性质来灵活地运用树剖
实现
我们先给出一些定义:
$f(x)$表示节点$x$在树上的父亲。
$dep(x)$表示节点$x$在树上的深度。
$size(x)$表示节点$x$的子树的节点个数。
$son(x)$表示节点$x$的 重儿子 。
$top(x)$表示节点$x$所在 重链 的顶部节点(深度最小)。
$id(x)$表示节点$x$的 $dfs$ 序 ,也是其在线段树中的编号。
$rk(x)$表示 $dfs$ 序所对应的节点编号,有$rk(dfs(x))=x$
首先第一遍$dfs$,对于每个节点,我们主要是求出它所在子树的大小并标记重儿子
void dfs1(int u, int fa){ size[u] = 1; //这个点本身size=1 for(int i = head[u]; i; i = e[i].next){ int v = e[i].to; if(v==fa) continue; dep[v] = dep[u] + 1, f[v] = u; dfs1(v, u), size[u] += size[v]; //子节点的size已被处理,用它来更新父节点的size if(size[v]>size[son[u]]) son[u] = v; //选取size最大的作为重儿子 } }
处理后如下图: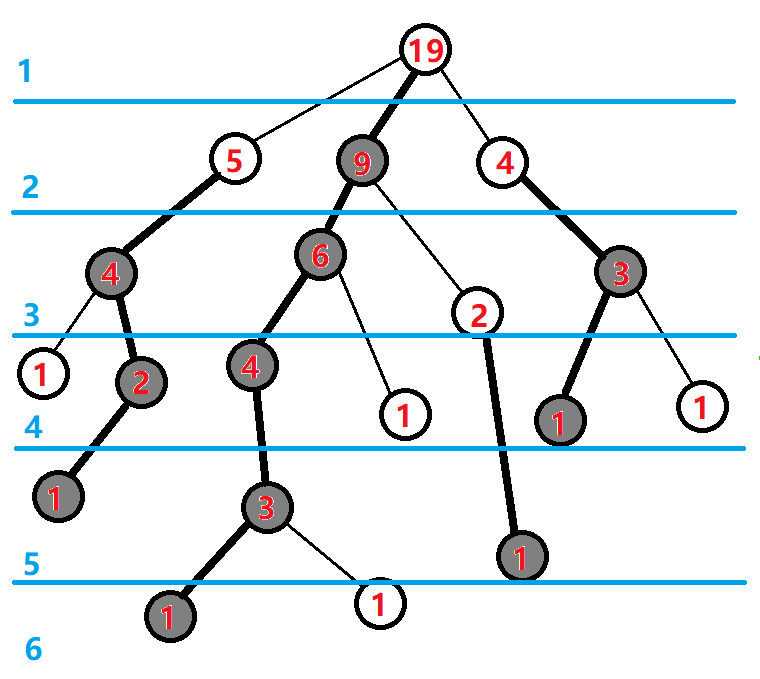
第二遍 dfs,然后连接重链,同时标记每一个节点的 dfs序,并且为了用数据结构来维护重链,我们在 dfs时保证一条重链上各个节点 dfs序连续
void dfs2(int u, int t){ //当前节点、重链顶端 top[u] = t, id[u] = ++cnt; //标记dfs序 rk[cnt] = u; //序号cnt对应节点u if(son[u]) dfs2(son[u], t); //我们选择优先进入重儿子来保证一条重链上各个节点dfs序连续 for(int i = head[u]; i; i = e[i].next){ int v = e[i].to; if(v==son[u]||v==f[u]) continue; dfs2(v, v); //一个点位于轻链底端,那么它的top必然是它本身 } }
可以结合下图理解一下:
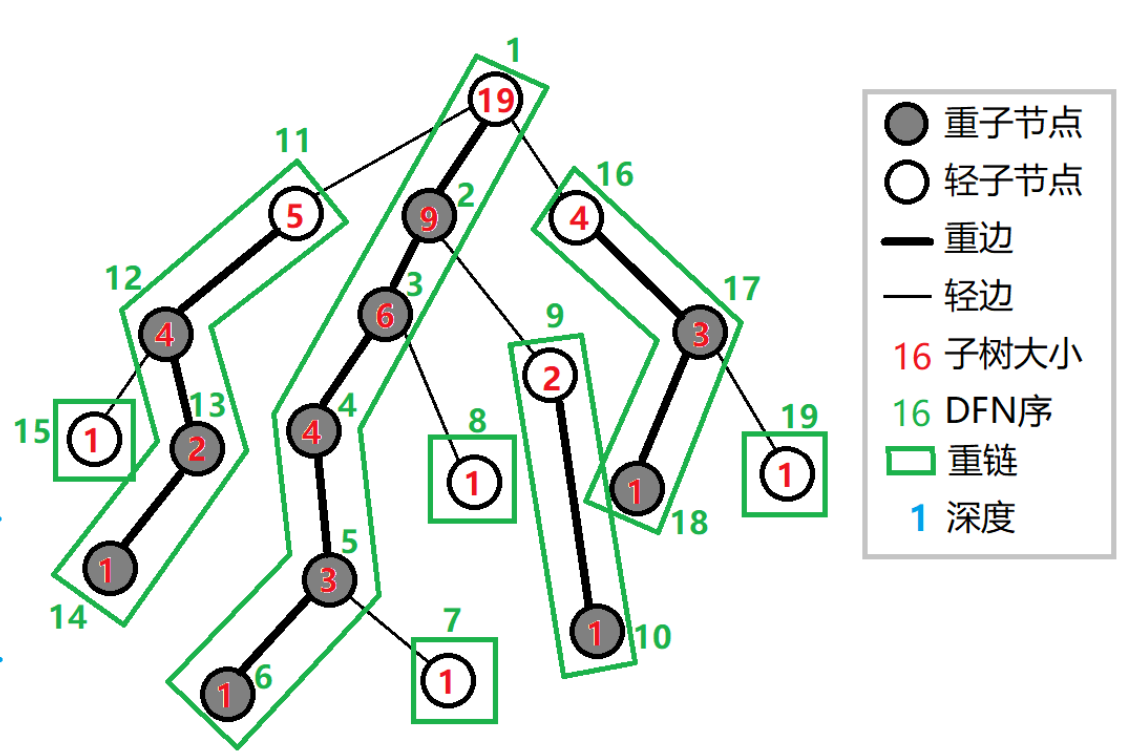
通过 $dfs$我们已经保证一条重链上各个节点$dfs$序连续,剖分完以后,每一条重链相当于一个区间,我们维护处理完的数据结构即可
常见应用
路径上维护
那么我们每次对$u,v$两个点进行询问
若两点在同一条链上,则直接在线段树上进行询问;若不在一条链上,则每次选择深度较大的链往上跳,直到两点在同一条链上
子树维护
有时会要求维护子树上的信息,譬如将以$x$为根的子树的所有结点的权值增加$v$
由于在$dfs$搜索时,子树的编号是连续的,根节点的编号到加上子树大小-1的区间即为子树区间,我们处理这段区间即可
求最近公共祖先
假设两点在同一条重链上,显然它们中深度较小的点即为它们的最近公共祖先
由这个我们得到种做法,即不断向上跳重链,当跳到同一条重链上时,深度较小的结点即为 $LCA$
向上跳重链时需要先跳所在重链顶端深度较大的那个
代码如下:
int lca(int u,int v){ while(top[u]!=top[v]){ if(dep[top[u]]<dep[top[v]]) swap(u,v); u = fa[top[u]]; } return dep[u]<dep[v] ? u : v; }
例题
待补~
参考自:
https://www.xuebuyuan.com/552070.html